冀教版(新)九上-28.3 圆心角与圆周角 第三课时【优质课件】
文档属性
| 名称 | 冀教版(新)九上-28.3 圆心角与圆周角 第三课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:47 | ||
图片预览








文档简介
(共22张PPT)
28.3 圆心角与圆周角
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
同弧所对的圆周角与圆心角有什么关系呢?直径与圆周角又有什么关系呢?我们今天就来探究探究 .
新课精讲
探索新知
1
知识点
直径所对的圆周角是直角
直径所对的圆周角是多少度?请说明理由.
总结
直径所对的圆周角是直角 .
探索新知
已知:如图,AB是⊙O的直径,D是圆上任意一点
(不与A,B重合),连接BD并延长到点C,使BD=
DC,连接AC,试判断△ABC的形状 .
例1
导引:连接AD,由AB是直径可得AD⊥BC,
再由BD=DC,可得AB=AC .
解:如图,连接AD .
∵AB是直径,∴∠ADB=90°,
∴AD⊥BC .
∵BD=DC,∴AB=AC,∴△ABC是等腰三角形.
探索新知
总 结
如果题目中有直径,常常添加辅助线,构造直径所对的圆周角,把问题转化为直角三角形的问题.
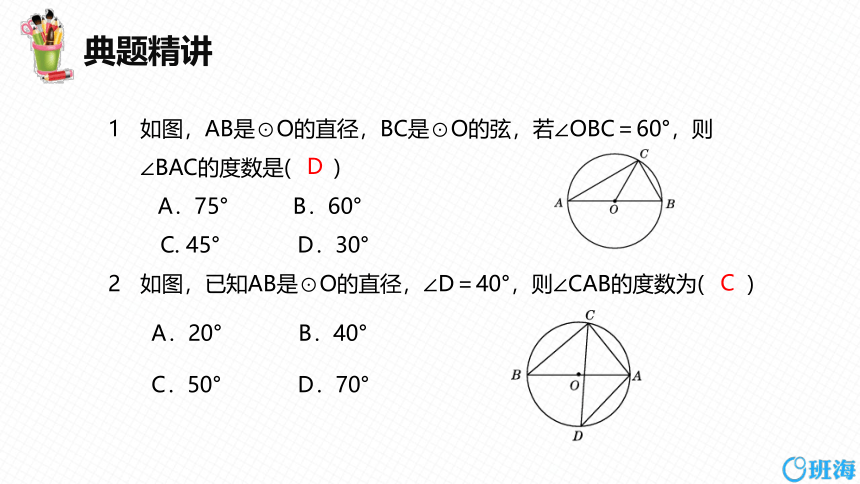
如图,AB是⊙O的直径,BC是⊙O的弦,若∠OBC=60°,则
∠BAC的度数是( )
A.75° B.60°
C. 45° D.30°
如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为( )
A.20° B.40°
C.50° D.70°
典题精讲
D
C
探索新知
2
知识点
90°的圆周角所对的弦是直径
90°的圆周角所对的弦是直径吗?请说明理由 .
总结
90°的圆周角所对的弦是直径 .
探索新知
例2 如图所示,已知CO、CB是⊙O′的弦,⊙O′与直角
坐标系的x,y轴相交于点B、A,若∠COB= 45°,
∠OBC= 75°,A点坐标为(0,2),求⊙O′的直径 .
分析:在平面直角坐标系中,∠AOB=90°,
故若连接AB的话,AB是⊙O′的直径,求AB即可 .
解:连接AB . 因为∠AOB=90°,所以AB是⊙O′的直径 . ∠A=∠C=180°-∠COB-∠OBC=180°-45°-75°=60°.
所以∠ABO=30°. 又A(0,2),所以OA=2,所以AB=2OA=4 .
即⊙O′的直径为4 .
探索新知
本题将圆与平面直角坐标系巧妙结合,并转化为三角形的有关知识解答,解答综合题的关键是找到它们的“结合点”,如本题中,对平面直角坐标系而言,有x轴⊥y轴;对△AOB而言,有∠AOB=90°;对⊙O′而言,由∠AOB=90°,得AB为⊙O′的直径,且∠A=∠C . 解答综合题还要注意,一般情况下,除了充分利用题目的已知条件外,还要挖掘图形中的隐含条件 .
总 结
典题精讲
1 下列结论正确的是( )
A.相等的圆心角所对的弦相等
B.等弦所对的弧相等
C.等弧所对的弦相等
D.垂直于弦的直线平分弦
2 从下列直角三角尺与圆弧的位置关系中,可判断圆弧为半圆的是( )
C
B
学以致用
小试牛刀
1 如图,AB是⊙O的直径,∠A=10°,则∠ABC=______.
80°
2 如图,AB是⊙O直径,CD是弦,∠ACD=40°,则∠BCD=_____,∠BOD=______.
50°
100°
小试牛刀
如图,AB是⊙O的直径,AC是弦,∠BAC=30°,则 的度数是( )
A.30° B.60° C.90° D.120°
D
4 如图,AB是⊙O的直径,AC是⊙O的弦,以OA为直径的⊙D与AC相交于点E,AC=10,求AE的长 .
解:连接EO,
∵OA为⊙D直径,∴∠AEO=90°,
∵AC是⊙O的弦,∴AE=EC,
∵AC=10,∴AE=5.
小试牛刀
如图,△ABC的3个顶点都在⊙O上,直径AD=4,∠ABC=∠DAC,
求AC的长 .
解:如图,连接CD,
∵AD是直径,
∴∠ACD=90°,
∵∠ABC=∠DAC,∠ADC=∠ABC,
∴∠ADC=∠DAC=45°,
∵直径AD=4,
∴AC=AD cos45°=2
小试牛刀
如图所示,AB,AC是⊙O的弦,AD⊥BC于D,交⊙O于F,AE
与⊙O的直径,试问两弦BE与CF的大小有何关系,说明理由.
BE=CF,理由:
∵AE为⊙O的直径,AD⊥BC
∴∠ABE=90°=∠ADC
∵∠AEB=∠ACB(同弧所对的圆周角相等),
∴∠BAE=∠CAF(等角的余角相等)
∴ =
∴BE=CF.
小试牛刀
如图所示,△ABC中,AC=BC,以AC为直径的⊙O交AB于E,作
△BCA的外角平分线CF交⊙O于F,连接EF,求证:EF=BC.
证明:∵CA=CB,∴∠B=∠A,
又∵∠DCA=2∠FCA,∠DCA=∠A+∠B=2∠A,
∴∠FCA=∠A.∴CF∥AB.
又∵∠FCA=∠FEA(同弧所对的圆周角相等),
∴∠FEA=∠B.∴BC∥EF.
∴四边形CFEB为平行四边形.∴EF=BC.
课堂小结
课堂小结
1.已知直径时,常添加辅助线构造直角三角形,即“见直径想直角”.题目中遇到直径时要考虑直径所对的圆周角为90°,遇到90°的圆周角时要考虑直角所对的弦为直径,这是圆中作辅助线的常用方法.
2.在解决圆的有关问题时,常常利用圆周角定理及其推论进行两种转化:一是利用同弧所对的圆周角相等,进行角与角之间的转化,二是将圆周角相等的问题转化为弦相等或弧相等的问题 .
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
28.3 圆心角与圆周角
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
同弧所对的圆周角与圆心角有什么关系呢?直径与圆周角又有什么关系呢?我们今天就来探究探究 .
新课精讲
探索新知
1
知识点
直径所对的圆周角是直角
直径所对的圆周角是多少度?请说明理由.
总结
直径所对的圆周角是直角 .
探索新知
已知:如图,AB是⊙O的直径,D是圆上任意一点
(不与A,B重合),连接BD并延长到点C,使BD=
DC,连接AC,试判断△ABC的形状 .
例1
导引:连接AD,由AB是直径可得AD⊥BC,
再由BD=DC,可得AB=AC .
解:如图,连接AD .
∵AB是直径,∴∠ADB=90°,
∴AD⊥BC .
∵BD=DC,∴AB=AC,∴△ABC是等腰三角形.
探索新知
总 结
如果题目中有直径,常常添加辅助线,构造直径所对的圆周角,把问题转化为直角三角形的问题.
如图,AB是⊙O的直径,BC是⊙O的弦,若∠OBC=60°,则
∠BAC的度数是( )
A.75° B.60°
C. 45° D.30°
如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为( )
A.20° B.40°
C.50° D.70°
典题精讲
D
C
探索新知
2
知识点
90°的圆周角所对的弦是直径
90°的圆周角所对的弦是直径吗?请说明理由 .
总结
90°的圆周角所对的弦是直径 .
探索新知
例2 如图所示,已知CO、CB是⊙O′的弦,⊙O′与直角
坐标系的x,y轴相交于点B、A,若∠COB= 45°,
∠OBC= 75°,A点坐标为(0,2),求⊙O′的直径 .
分析:在平面直角坐标系中,∠AOB=90°,
故若连接AB的话,AB是⊙O′的直径,求AB即可 .
解:连接AB . 因为∠AOB=90°,所以AB是⊙O′的直径 . ∠A=∠C=180°-∠COB-∠OBC=180°-45°-75°=60°.
所以∠ABO=30°. 又A(0,2),所以OA=2,所以AB=2OA=4 .
即⊙O′的直径为4 .
探索新知
本题将圆与平面直角坐标系巧妙结合,并转化为三角形的有关知识解答,解答综合题的关键是找到它们的“结合点”,如本题中,对平面直角坐标系而言,有x轴⊥y轴;对△AOB而言,有∠AOB=90°;对⊙O′而言,由∠AOB=90°,得AB为⊙O′的直径,且∠A=∠C . 解答综合题还要注意,一般情况下,除了充分利用题目的已知条件外,还要挖掘图形中的隐含条件 .
总 结
典题精讲
1 下列结论正确的是( )
A.相等的圆心角所对的弦相等
B.等弦所对的弧相等
C.等弧所对的弦相等
D.垂直于弦的直线平分弦
2 从下列直角三角尺与圆弧的位置关系中,可判断圆弧为半圆的是( )
C
B
学以致用
小试牛刀
1 如图,AB是⊙O的直径,∠A=10°,则∠ABC=______.
80°
2 如图,AB是⊙O直径,CD是弦,∠ACD=40°,则∠BCD=_____,∠BOD=______.
50°
100°
小试牛刀
如图,AB是⊙O的直径,AC是弦,∠BAC=30°,则 的度数是( )
A.30° B.60° C.90° D.120°
D
4 如图,AB是⊙O的直径,AC是⊙O的弦,以OA为直径的⊙D与AC相交于点E,AC=10,求AE的长 .
解:连接EO,
∵OA为⊙D直径,∴∠AEO=90°,
∵AC是⊙O的弦,∴AE=EC,
∵AC=10,∴AE=5.
小试牛刀
如图,△ABC的3个顶点都在⊙O上,直径AD=4,∠ABC=∠DAC,
求AC的长 .
解:如图,连接CD,
∵AD是直径,
∴∠ACD=90°,
∵∠ABC=∠DAC,∠ADC=∠ABC,
∴∠ADC=∠DAC=45°,
∵直径AD=4,
∴AC=AD cos45°=2
小试牛刀
如图所示,AB,AC是⊙O的弦,AD⊥BC于D,交⊙O于F,AE
与⊙O的直径,试问两弦BE与CF的大小有何关系,说明理由.
BE=CF,理由:
∵AE为⊙O的直径,AD⊥BC
∴∠ABE=90°=∠ADC
∵∠AEB=∠ACB(同弧所对的圆周角相等),
∴∠BAE=∠CAF(等角的余角相等)
∴ =
∴BE=CF.
小试牛刀
如图所示,△ABC中,AC=BC,以AC为直径的⊙O交AB于E,作
△BCA的外角平分线CF交⊙O于F,连接EF,求证:EF=BC.
证明:∵CA=CB,∴∠B=∠A,
又∵∠DCA=2∠FCA,∠DCA=∠A+∠B=2∠A,
∴∠FCA=∠A.∴CF∥AB.
又∵∠FCA=∠FEA(同弧所对的圆周角相等),
∴∠FEA=∠B.∴BC∥EF.
∴四边形CFEB为平行四边形.∴EF=BC.
课堂小结
课堂小结
1.已知直径时,常添加辅助线构造直角三角形,即“见直径想直角”.题目中遇到直径时要考虑直径所对的圆周角为90°,遇到90°的圆周角时要考虑直角所对的弦为直径,这是圆中作辅助线的常用方法.
2.在解决圆的有关问题时,常常利用圆周角定理及其推论进行两种转化:一是利用同弧所对的圆周角相等,进行角与角之间的转化,二是将圆周角相等的问题转化为弦相等或弧相等的问题 .
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
