冀教版(新)九上-28.3 圆心角与圆周角 第四课时【优质课件】
文档属性
| 名称 | 冀教版(新)九上-28.3 圆心角与圆周角 第四课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:47 | ||
图片预览










文档简介
(共34张PPT)
28.3 圆心角与圆周角
第4课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
前边我学习了圆的内接三角形,圆的内接三角形有哪些性质呢?今天我们探究的圆的内接四边形的性质,我们根据圆内接三角形的定义,想一想如何给圆内接四边形下定义呢?
新课精讲
探索新知
1
知识点
圆内接多边形
下面,我们探究四边形与圆的关系 .
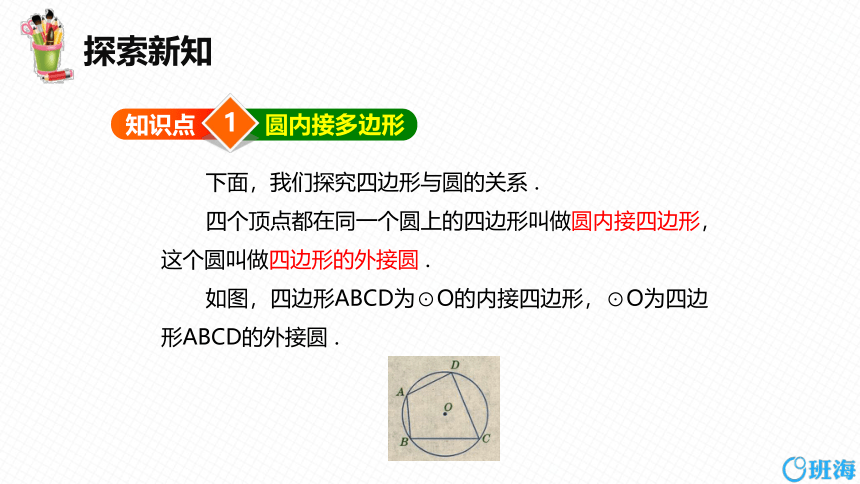
四个顶点都在同一个圆上的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆 .
如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆 .
探索新知
定义:四个顶点都在同一个圆上的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆.
探索新知
如果圆内接四边形ABCD的对角线交点恰好是该圆的圆心,则四边形ABCD一定是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
例1
分析:由圆内接四边形ABCD的对角线交点恰好是该圆的圆心,根据直径所对的圆周角是直角,可求得四边形ABCD的四个内角都是直角,即可判定四边形ABCD一定是矩形 .
解:∵圆内接四边形ABCD的对角线交点恰好是该圆的圆心,∴∠A=∠B=∠C=∠D=90°,∴四边形ABCD一定是矩形 . 故选B .
B
探索新知
总 结
本题根据直径所对的圆周角是90°来解答 .
典题精讲
1 下列说法正确的是( )
A.顶点在圆周上的角叫做圆周角
B.圆内接平行四边形一定是矩形
C.平分弦的直径一定垂直于弦
D.与直径垂直的直线是圆的切线
2 下列多边形中一定有外接圆的是( )
A.三角形 B.四边形
C.五边形 D.六边形
B
A
探索新知
2
知识点
圆内接四边形对角互补
如图,四边形ABCD为⊙O的内接四边形 .
(1) 和 所对的圆心角之和等于多少度?
∠ABC和∠ADC之间具有怎样的关系?
(2)∠BAD和∠BCD之间具有怎样的关系?
提出你的猜想,并和大家进行交流 .
探索新知
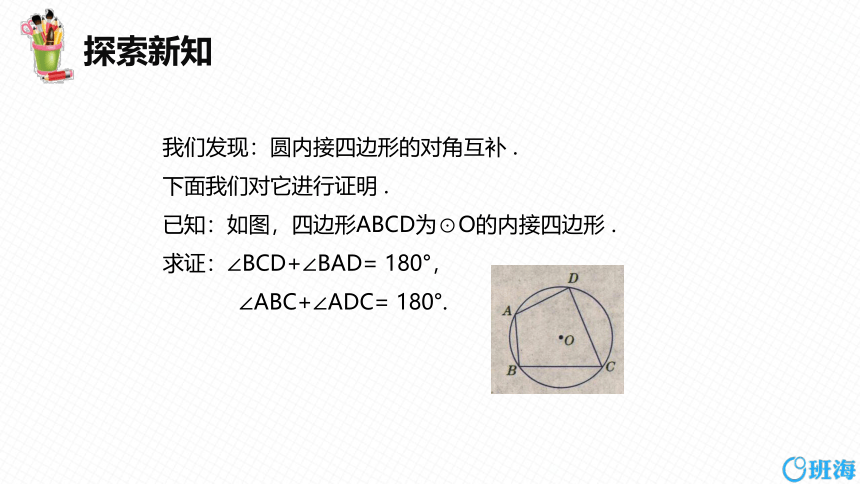
我们发现:圆内接四边形的对角互补 .
下面我们对它进行证明 .
已知:如图,四边形ABCD为⊙O的内接四边形 .
求证:∠BCD+∠BAD= 180°,
∠ABC+∠ADC= 180°.
探索新知
证明:如图,连接OB,OD.
∵ 与 所对的圆心角之和为360°,
∠BCD和∠BAD分别为 和 所对的
圆周角,
∴∠BCD+∠BAD= 180° .
同理可证,∠ABC+∠ADC=180° .
探索新知
探索新知
圆内接四边形的对角互补 .
总 结
探索新知
例2 已知:如图,四边形ABCD为⊙O的内接四边形,∠DCE为四边
形ABCD的一个外角 . 求证:∠DCE=∠BAD .
证明:∵四边形ABCD为⊙O的内接四边形,
∴∠BAD+∠BCD= 180° .
∵∠BCD+∠DCE= 180°,
∴∠DCE=∠BAD .
探索新知
(1)在求圆中的某一个圆周角时,根据“圆内接四边形的对角互补”,可以转化为求其所在的内接四边形的对角的度数.
(2)圆内接四边形的一组对角其实是圆中一条弦所对的两类圆周角.
总 结
典题精讲
如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°, 则∠BCD的度数为( )
A.50°
B.80°
C.100°
D.130°
D
典题精讲
在圆内接四边形ABCD中,已知∠A=70°,则∠C等于( )
A.20° B.30° C.70° D.110°
3 下列命题:
(1)圆内接梯形是等腰梯形;
(2)圆内接平行四边形是矩形;
(3)圆内接矩形是正方形;
(4)圆内接菱形是正方形.
其中真命题有( )
A.1个 B.2个 C.3个 D.4个
D
C
探索新知
3
知识点
圆内接四边形的外角等于其内对角
推论:圆内接四边形的一个外角等于它的内对角.
探索新知
例3 如图,四边形ABCD内接于⊙O,若四边形ABCD的外角
∠DCE=70°,则∠BAD的度数为( )
A. 140° B. 110°
C. 220° D. 70°
分析:根据圆内接四边形的性质:圆内接四边形的外角等于它的内对角即可解答 .
解:∵四边形ABCD内接于⊙O, ∴∠BAD=∠DCE=70°. 故选D .
D
探索新知
此题考查了圆内接四边形的性质,熟记圆内接
四边形的外角等于它的内对角是解题的关键 .
总 结
典题精讲
如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE=_______.
如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F=_______.
(第1题)
(第2题)
105°
40°
学以致用
小试牛刀
1.在圆内接四边形ABCD中,若∠A=45°,∠B=67.5°,则∠D等于( )
A.67.5° B.135° C.112.5° D.45°
2.四边形ABCD内接于圆,∠A,∠B,∠C,∠D的度数比可能是( )
A.1∶2∶3∶4 B.7∶5∶10∶8
C.13∶1∶5∶17 D.1∶3∶2∶4
C
C
小试牛刀
3.如图所示,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( )
A.45° B.50° C.60° D.75°
4.如图所示,在圆O的内接四边形ABCD中,BC=DC,∠BOC=130°,则∠BAD的度数是( )
A.120° B.130° C.140° D.150°
C
B
小试牛刀
5.如图所示,AB为⊙O的直径,点C,D在⊙O上.若∠AOD=30°,
则∠BCD的度数是( )
A.75° B.95° C.105° D.115°
6.如图所示,△ABC内接于⊙O,∠OBC=40°,则∠A的度数为( )
A.80° B.100° C.110° D.130°
D
C
小试牛刀
7.如图所示,在⊙O的内接四边形ABCD中,∠A=115°,则
∠BOD等于_______.
8.如图所示,AB是⊙O的直径,C,D是AB上两点,∠ADC=
120°,则∠BAC等于______.
130°
30°
⌒
小试牛刀
9.如图所示,四边形ABCD为⊙O的内接四边形,并且AD是⊙O的直径,C是 的中点,AB和DC的延长线交于⊙O外一点E . 求证:BC=EC .
证明:如图,连结AC .
∵AD是⊙O的直径,∴AC⊥DE .
∵C是 的中点,∴∠ADC=∠AED .
∵∠EBC=∠D,∴∠EBC=∠E,∴BC=EC .
小试牛刀
10.如图所示,⊙C过原点,且与两坐标轴分别交于点A,B,点A的坐标为(0,3),M是劣弧OB上一点,∠BMO=120°. 求⊙C的半径长.
解:∵四边形ABMO是⊙C的内接四边形,∠BMO=120°,
∴∠BAO=60°.
∵AB是⊙C的直径, ∴∠AOB=90°,
∴∠ABO=90°-∠BAO=90°-60°=30° .
∵点A的坐标为(0,3),
∴OA=3,∴AB=2OA=6,∴⊙C的半径长为3 .
小试牛刀
课堂小结
课堂小结
圆内接四边形的角的“三种关系”:
(1)对角互补,若四边形ABCD为⊙O的内接四边形,则∠A+∠C=180°,∠B+∠D=180°.
(2)四个内角的和是360°,若四边形ABCD为⊙O的内接四边形,则∠A+∠B+∠C+∠D=360°.
(3)任一外角与其相邻的内角的对角相等,简称圆内接四边形的外角等于其内对角.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
28.3 圆心角与圆周角
第4课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
前边我学习了圆的内接三角形,圆的内接三角形有哪些性质呢?今天我们探究的圆的内接四边形的性质,我们根据圆内接三角形的定义,想一想如何给圆内接四边形下定义呢?
新课精讲
探索新知
1
知识点
圆内接多边形
下面,我们探究四边形与圆的关系 .
四个顶点都在同一个圆上的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆 .
如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆 .
探索新知
定义:四个顶点都在同一个圆上的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆.
探索新知
如果圆内接四边形ABCD的对角线交点恰好是该圆的圆心,则四边形ABCD一定是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
例1
分析:由圆内接四边形ABCD的对角线交点恰好是该圆的圆心,根据直径所对的圆周角是直角,可求得四边形ABCD的四个内角都是直角,即可判定四边形ABCD一定是矩形 .
解:∵圆内接四边形ABCD的对角线交点恰好是该圆的圆心,∴∠A=∠B=∠C=∠D=90°,∴四边形ABCD一定是矩形 . 故选B .
B
探索新知
总 结
本题根据直径所对的圆周角是90°来解答 .
典题精讲
1 下列说法正确的是( )
A.顶点在圆周上的角叫做圆周角
B.圆内接平行四边形一定是矩形
C.平分弦的直径一定垂直于弦
D.与直径垂直的直线是圆的切线
2 下列多边形中一定有外接圆的是( )
A.三角形 B.四边形
C.五边形 D.六边形
B
A
探索新知
2
知识点
圆内接四边形对角互补
如图,四边形ABCD为⊙O的内接四边形 .
(1) 和 所对的圆心角之和等于多少度?
∠ABC和∠ADC之间具有怎样的关系?
(2)∠BAD和∠BCD之间具有怎样的关系?
提出你的猜想,并和大家进行交流 .
探索新知
我们发现:圆内接四边形的对角互补 .
下面我们对它进行证明 .
已知:如图,四边形ABCD为⊙O的内接四边形 .
求证:∠BCD+∠BAD= 180°,
∠ABC+∠ADC= 180°.
探索新知
证明:如图,连接OB,OD.
∵ 与 所对的圆心角之和为360°,
∠BCD和∠BAD分别为 和 所对的
圆周角,
∴∠BCD+∠BAD= 180° .
同理可证,∠ABC+∠ADC=180° .
探索新知
探索新知
圆内接四边形的对角互补 .
总 结
探索新知
例2 已知:如图,四边形ABCD为⊙O的内接四边形,∠DCE为四边
形ABCD的一个外角 . 求证:∠DCE=∠BAD .
证明:∵四边形ABCD为⊙O的内接四边形,
∴∠BAD+∠BCD= 180° .
∵∠BCD+∠DCE= 180°,
∴∠DCE=∠BAD .
探索新知
(1)在求圆中的某一个圆周角时,根据“圆内接四边形的对角互补”,可以转化为求其所在的内接四边形的对角的度数.
(2)圆内接四边形的一组对角其实是圆中一条弦所对的两类圆周角.
总 结
典题精讲
如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°, 则∠BCD的度数为( )
A.50°
B.80°
C.100°
D.130°
D
典题精讲
在圆内接四边形ABCD中,已知∠A=70°,则∠C等于( )
A.20° B.30° C.70° D.110°
3 下列命题:
(1)圆内接梯形是等腰梯形;
(2)圆内接平行四边形是矩形;
(3)圆内接矩形是正方形;
(4)圆内接菱形是正方形.
其中真命题有( )
A.1个 B.2个 C.3个 D.4个
D
C
探索新知
3
知识点
圆内接四边形的外角等于其内对角
推论:圆内接四边形的一个外角等于它的内对角.
探索新知
例3 如图,四边形ABCD内接于⊙O,若四边形ABCD的外角
∠DCE=70°,则∠BAD的度数为( )
A. 140° B. 110°
C. 220° D. 70°
分析:根据圆内接四边形的性质:圆内接四边形的外角等于它的内对角即可解答 .
解:∵四边形ABCD内接于⊙O, ∴∠BAD=∠DCE=70°. 故选D .
D
探索新知
此题考查了圆内接四边形的性质,熟记圆内接
四边形的外角等于它的内对角是解题的关键 .
总 结
典题精讲
如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE=_______.
如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F=_______.
(第1题)
(第2题)
105°
40°
学以致用
小试牛刀
1.在圆内接四边形ABCD中,若∠A=45°,∠B=67.5°,则∠D等于( )
A.67.5° B.135° C.112.5° D.45°
2.四边形ABCD内接于圆,∠A,∠B,∠C,∠D的度数比可能是( )
A.1∶2∶3∶4 B.7∶5∶10∶8
C.13∶1∶5∶17 D.1∶3∶2∶4
C
C
小试牛刀
3.如图所示,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( )
A.45° B.50° C.60° D.75°
4.如图所示,在圆O的内接四边形ABCD中,BC=DC,∠BOC=130°,则∠BAD的度数是( )
A.120° B.130° C.140° D.150°
C
B
小试牛刀
5.如图所示,AB为⊙O的直径,点C,D在⊙O上.若∠AOD=30°,
则∠BCD的度数是( )
A.75° B.95° C.105° D.115°
6.如图所示,△ABC内接于⊙O,∠OBC=40°,则∠A的度数为( )
A.80° B.100° C.110° D.130°
D
C
小试牛刀
7.如图所示,在⊙O的内接四边形ABCD中,∠A=115°,则
∠BOD等于_______.
8.如图所示,AB是⊙O的直径,C,D是AB上两点,∠ADC=
120°,则∠BAC等于______.
130°
30°
⌒
小试牛刀
9.如图所示,四边形ABCD为⊙O的内接四边形,并且AD是⊙O的直径,C是 的中点,AB和DC的延长线交于⊙O外一点E . 求证:BC=EC .
证明:如图,连结AC .
∵AD是⊙O的直径,∴AC⊥DE .
∵C是 的中点,∴∠ADC=∠AED .
∵∠EBC=∠D,∴∠EBC=∠E,∴BC=EC .
小试牛刀
10.如图所示,⊙C过原点,且与两坐标轴分别交于点A,B,点A的坐标为(0,3),M是劣弧OB上一点,∠BMO=120°. 求⊙C的半径长.
解:∵四边形ABMO是⊙C的内接四边形,∠BMO=120°,
∴∠BAO=60°.
∵AB是⊙C的直径, ∴∠AOB=90°,
∴∠ABO=90°-∠BAO=90°-60°=30° .
∵点A的坐标为(0,3),
∴OA=3,∴AB=2OA=6,∴⊙C的半径长为3 .
小试牛刀
课堂小结
课堂小结
圆内接四边形的角的“三种关系”:
(1)对角互补,若四边形ABCD为⊙O的内接四边形,则∠A+∠C=180°,∠B+∠D=180°.
(2)四个内角的和是360°,若四边形ABCD为⊙O的内接四边形,则∠A+∠B+∠C+∠D=360°.
(3)任一外角与其相邻的内角的对角相等,简称圆内接四边形的外角等于其内对角.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
