冀教版(新)九上-28.3 圆心角与圆周角 第一课时【优质课件】
文档属性
| 名称 | 冀教版(新)九上-28.3 圆心角与圆周角 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:47 | ||
图片预览








文档简介
(共30张PPT)
28.3 圆心角与圆周角
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
观察扇子的图形,你有什么发现?
新课精讲
探索新知
1
知识点
圆心角及它所对弧的度数的关系
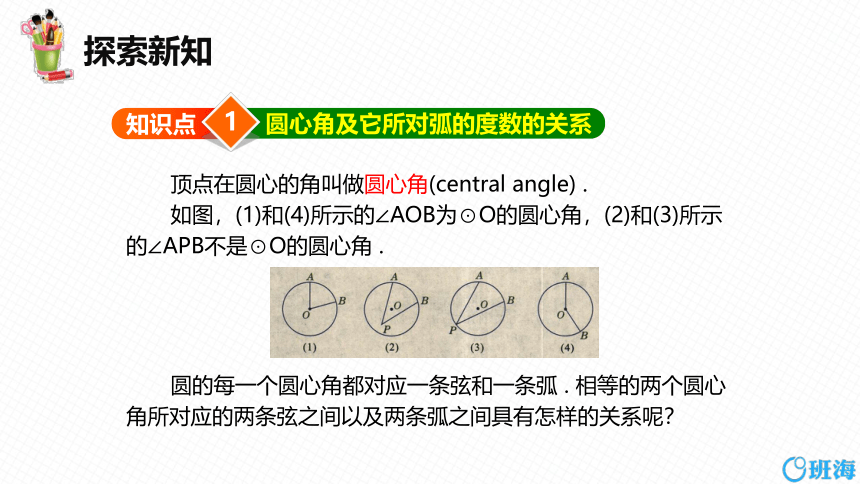
顶点在圆心的角叫做圆心角(central angle) .
如图,(1)和(4)所示的∠AOB为⊙O的圆心角,(2)和(3)所示的∠APB不是⊙O的圆心角 .
圆的每一个圆心角都对应一条弦和一条弧 . 相等的两个圆心角所对应的两条弦之间以及两条弧之间具有怎样的关系呢?
探索新知
定义:
顶点在圆心的角叫做圆心角.一个角是圆心角,必须具备顶点在圆心这一特征.
要点精析:圆心角的条件:
(1)顶点在圆心;(2)两边和圆相交.
拓展:(1)1°的圆心角所对的弧叫做1°的弧.这样,n°的圆心角所对的弧就是n°的弧.
(2)圆心角的度数与它所对的弧的度数是一致(或相等)的,即圆心角的度数等于它所对弧的度数.注意这里仅指度数相等 .
探索新知
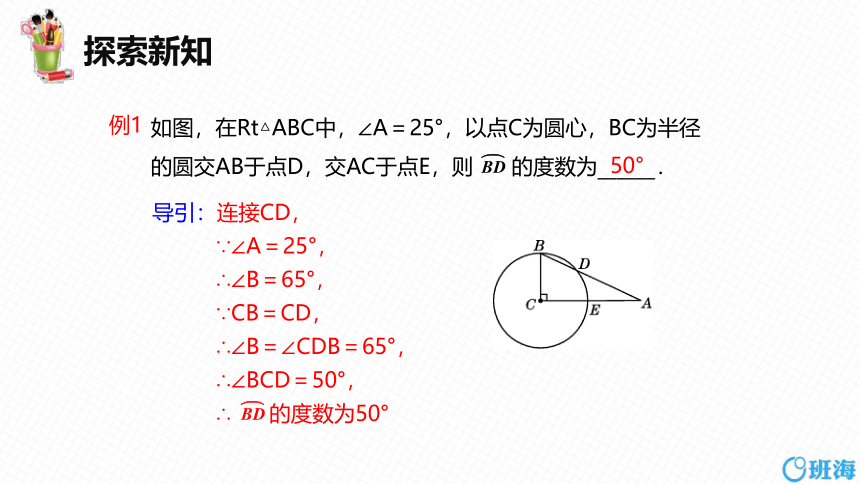
如图,在Rt△ABC中,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则 的度数为______.
例1
50°
导引:连接CD,
∵∠A=25°,
∴∠B=65°,
∵CB=CD,
∴∠B=∠CDB=65°,
∴∠BCD=50°,
∴ 的度数为50°
探索新知
结 论
根据弧的度数与该弧所对的圆心角的度数相等,在求弧的度数时,一般将其转化为求该弧所对的圆心角的度数,体现了数学中的转化思想.
典题精讲
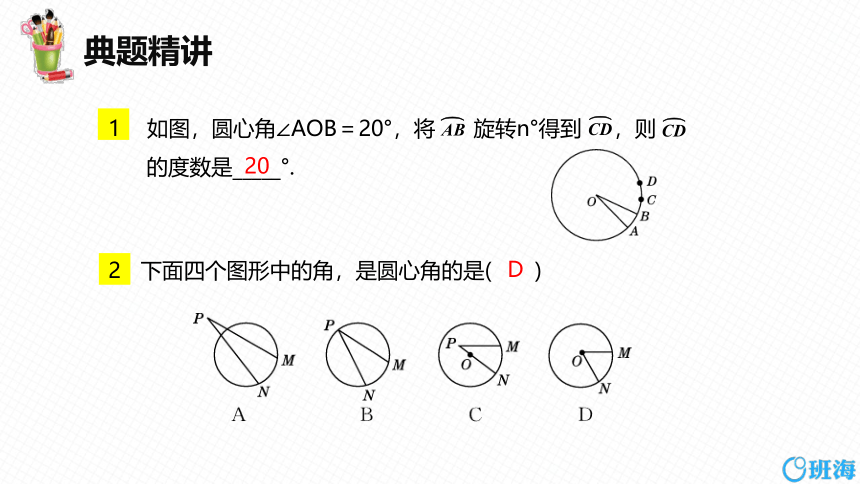
如图,圆心角∠AOB=20°,将 旋转n°得到 ,则
的度数是_____°.
20
下面四个图形中的角,是圆心角的是( )
D
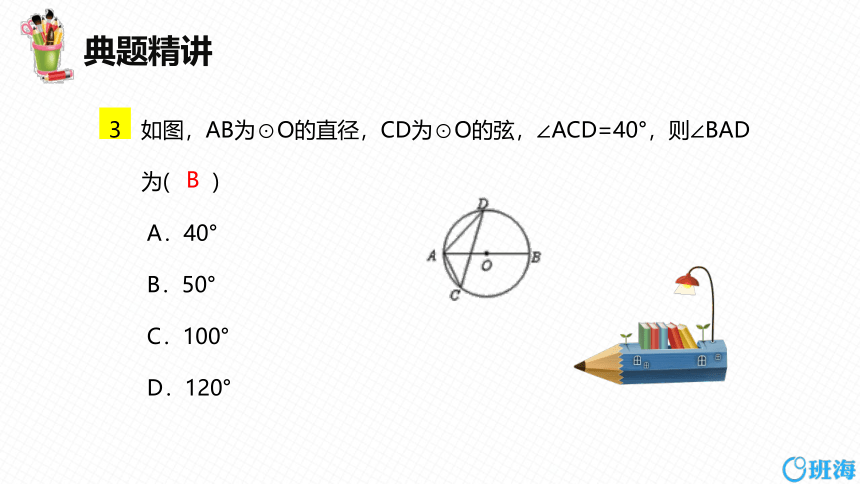
如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=40°,则∠BAD为( )
A.40°
B.50°
C.100°
D.120°
典题精讲
B
探索新知
2
知识点
圆心角定理
如图,在⊙O中,∠AOB=∠COD .
(1)猜想弦AB,CD以及
之间各具有怎样 的关系 .
(2)请用图形的旋转说明你的猜想 .
事实上,设∠AOC=α,将△AOB顺时针旋转α,则AO与CO重合, BO与DO重合 . 从而AB与CD重合,
重合 . 所以AB = CD,
结论:在同圆或等圆中,相等的圆心角所对的弦相等,所对的弧也相等 .
探索新知
例2 如图所示,AB和CD是两条直径,弦CE∥AB,求证:弧AD=弧AE .
分析:要证明弧AD=弧AE,需证明
∠AOD=∠AOE,由已知CE∥
AB,所以∠AOD=∠OCE,
∠AOE=∠OEC,又因为OC=OE,
可以知道∠OCE=∠OEC .
证明:连接OE . ∵OC=OE,∴∠OCE=∠OEC .
∵CE∥AB,∴∠AOD=∠OCE,∠AOE=∠OEC,
∴∠AOD=∠AOE,∴弧AD=弧AE .
探索新知
本题的解题关键是灵活运用圆心角、弧、弦间的关系,推出角相等,有角相等得弧相等 .
总 结
典题精讲
1 如图,在⊙O中, .求证:AC=BD .
证明:∵在⊙O中,弦AB=CD,
∴弧AB=弧CD,
∵弧BC=弧CB,
∴弧AC=弧BD .
典题精讲
2 下列命题是真命题的是( )
A. 相等的圆心角所对的弧相等,所对的弦也相等
B. 度数相等的弧是等弧
C. 三点确定一个圆
D. 圆周角是直角所对弦是直径
如图,AB是⊙O的直径,若∠COA=∠DOB=60°,则与线段AO
长度相等的线段有( )
A.3条 B.4条
C.5条 D.6条
D
D
探索新知
3
知识点
圆心角定理的推论
在同圆或等圆中,若两条弧(或弦)相等,则它们所对的圆心角是否相等,所对的弦(或弧)是否相等?试说明理由 .
探索新知
在同圆或等圆中,两个圆心角及其所对应的两条弦和所对应的两条弧这三组量中,只要有一组量相等,其他两组量就分别相等 .
结 论
探索新知
例3 已知:如图,AB为⊙O的直径,点M,N分别在AO,BO上,CM⊥
AB,DN⊥AB,分别交⊙O于点C,D,且
求证:CM=DN .
证明:如图,连接OC,OD .
在Rt△CMO和Rt△DNO中,
∴CM⊥AB,DN⊥AB,
∴∠CMO =∠DNO =90°.
又∵OC=OD,∠MOC=∠NOD, ∴Rt△CMO≌Rt△DNO . ∴CM= DN .
探索新知
在同一个圆中,弧、弦和圆心角中只要有一组量相等,就能推出另两组量相等.线段有和差,弧也有和差.
总 结
典题精讲
1 如图所示,在⊙O中, ,则在①AB=CD;②AC=BD;③∠AOC=∠BOD;④ 中,正确的个数是( )
A.1
B.2
C.3
D.4
D
典题精讲
在⊙O中,M,N分别为弦AB,CD的中点,如果OM=ON,那么在结论:①AB=CD;② ③∠AOB=∠COD中,正确的是( )
A.①② B.①③ C.②③ D.①②③
如图,在⊙O中,点C是 的中点,∠A=50°,则∠BOC=( )
A.40° B.45°
C.50° D.60°
D
A
学以致用
小试牛刀
1 如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则 BD 的度数为( )
A.25° B.30° C.50° D.65°
⌒
C
小试牛刀
下列说法中,正确的是( )
A.等弦所对的弧相等
B.等弧所对的弦相等
C.圆心角相等,所对的弦相等
D.弦相等,所对的圆心角相等
3 在⊙O中,圆心角∠AOB=2∠COD,则AB与CD的关系是( )
A. AB=2CD B. AB>2CD
C. AB< 2CD D. 不能确定
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
B
A
小试牛刀
4 如图,AB,CD是⊙O的两条弦 .
(1)如果AB=CD,那么________, _______________ .
(2)如果AB=CD,那么________, _______________ .
(3)如果∠AOB=∠COD,那么________, _________ .
(4)如果AB=CD,OE⊥AB,OF⊥CD,垂足分别为E,F,OE与
OF相等吗?为什么?
⌒
⌒
∠AOB=∠COD
AB=CD
∠AOB=∠COD
AB=CD
解:OE=OF,理由如下:
∵AB=CD,∴易证△ABO≌△CDO .
∴可证Rt△AOE≌Rt△COF,∴可得OE=OF .
小试牛刀
如图,在⊙O中,AB=AC,∠ACB=60°. 求证:∠AOB=∠BOC=
∠AOC .
⌒
⌒
证明:∵AB=AC,
∴AB=AC,△ABC是等腰三角形 .
又∠ACB=60°,
∴△ABC是等边三角形,AB=BC=CA .
∴∠AOB=∠BOC=∠AOC .
⌒
⌒
课堂小结
课堂小结
同一圆中证明两弦相等的“四种方法”:
(1)若两弦位于两个不同的三角形中,证明两弦所在的三角形全等.
(2)若两弦位于同一个三角形中,根据等角对等边证明两弦相等.
(3)在同一圆中证明两弦所对的弧相等(同一类弧).
(4)证明两弦所对的圆心角相等.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
28.3 圆心角与圆周角
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
观察扇子的图形,你有什么发现?
新课精讲
探索新知
1
知识点
圆心角及它所对弧的度数的关系
顶点在圆心的角叫做圆心角(central angle) .
如图,(1)和(4)所示的∠AOB为⊙O的圆心角,(2)和(3)所示的∠APB不是⊙O的圆心角 .
圆的每一个圆心角都对应一条弦和一条弧 . 相等的两个圆心角所对应的两条弦之间以及两条弧之间具有怎样的关系呢?
探索新知
定义:
顶点在圆心的角叫做圆心角.一个角是圆心角,必须具备顶点在圆心这一特征.
要点精析:圆心角的条件:
(1)顶点在圆心;(2)两边和圆相交.
拓展:(1)1°的圆心角所对的弧叫做1°的弧.这样,n°的圆心角所对的弧就是n°的弧.
(2)圆心角的度数与它所对的弧的度数是一致(或相等)的,即圆心角的度数等于它所对弧的度数.注意这里仅指度数相等 .
探索新知
如图,在Rt△ABC中,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则 的度数为______.
例1
50°
导引:连接CD,
∵∠A=25°,
∴∠B=65°,
∵CB=CD,
∴∠B=∠CDB=65°,
∴∠BCD=50°,
∴ 的度数为50°
探索新知
结 论
根据弧的度数与该弧所对的圆心角的度数相等,在求弧的度数时,一般将其转化为求该弧所对的圆心角的度数,体现了数学中的转化思想.
典题精讲
如图,圆心角∠AOB=20°,将 旋转n°得到 ,则
的度数是_____°.
20
下面四个图形中的角,是圆心角的是( )
D
如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=40°,则∠BAD为( )
A.40°
B.50°
C.100°
D.120°
典题精讲
B
探索新知
2
知识点
圆心角定理
如图,在⊙O中,∠AOB=∠COD .
(1)猜想弦AB,CD以及
之间各具有怎样 的关系 .
(2)请用图形的旋转说明你的猜想 .
事实上,设∠AOC=α,将△AOB顺时针旋转α,则AO与CO重合, BO与DO重合 . 从而AB与CD重合,
重合 . 所以AB = CD,
结论:在同圆或等圆中,相等的圆心角所对的弦相等,所对的弧也相等 .
探索新知
例2 如图所示,AB和CD是两条直径,弦CE∥AB,求证:弧AD=弧AE .
分析:要证明弧AD=弧AE,需证明
∠AOD=∠AOE,由已知CE∥
AB,所以∠AOD=∠OCE,
∠AOE=∠OEC,又因为OC=OE,
可以知道∠OCE=∠OEC .
证明:连接OE . ∵OC=OE,∴∠OCE=∠OEC .
∵CE∥AB,∴∠AOD=∠OCE,∠AOE=∠OEC,
∴∠AOD=∠AOE,∴弧AD=弧AE .
探索新知
本题的解题关键是灵活运用圆心角、弧、弦间的关系,推出角相等,有角相等得弧相等 .
总 结
典题精讲
1 如图,在⊙O中, .求证:AC=BD .
证明:∵在⊙O中,弦AB=CD,
∴弧AB=弧CD,
∵弧BC=弧CB,
∴弧AC=弧BD .
典题精讲
2 下列命题是真命题的是( )
A. 相等的圆心角所对的弧相等,所对的弦也相等
B. 度数相等的弧是等弧
C. 三点确定一个圆
D. 圆周角是直角所对弦是直径
如图,AB是⊙O的直径,若∠COA=∠DOB=60°,则与线段AO
长度相等的线段有( )
A.3条 B.4条
C.5条 D.6条
D
D
探索新知
3
知识点
圆心角定理的推论
在同圆或等圆中,若两条弧(或弦)相等,则它们所对的圆心角是否相等,所对的弦(或弧)是否相等?试说明理由 .
探索新知
在同圆或等圆中,两个圆心角及其所对应的两条弦和所对应的两条弧这三组量中,只要有一组量相等,其他两组量就分别相等 .
结 论
探索新知
例3 已知:如图,AB为⊙O的直径,点M,N分别在AO,BO上,CM⊥
AB,DN⊥AB,分别交⊙O于点C,D,且
求证:CM=DN .
证明:如图,连接OC,OD .
在Rt△CMO和Rt△DNO中,
∴CM⊥AB,DN⊥AB,
∴∠CMO =∠DNO =90°.
又∵OC=OD,∠MOC=∠NOD, ∴Rt△CMO≌Rt△DNO . ∴CM= DN .
探索新知
在同一个圆中,弧、弦和圆心角中只要有一组量相等,就能推出另两组量相等.线段有和差,弧也有和差.
总 结
典题精讲
1 如图所示,在⊙O中, ,则在①AB=CD;②AC=BD;③∠AOC=∠BOD;④ 中,正确的个数是( )
A.1
B.2
C.3
D.4
D
典题精讲
在⊙O中,M,N分别为弦AB,CD的中点,如果OM=ON,那么在结论:①AB=CD;② ③∠AOB=∠COD中,正确的是( )
A.①② B.①③ C.②③ D.①②③
如图,在⊙O中,点C是 的中点,∠A=50°,则∠BOC=( )
A.40° B.45°
C.50° D.60°
D
A
学以致用
小试牛刀
1 如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则 BD 的度数为( )
A.25° B.30° C.50° D.65°
⌒
C
小试牛刀
下列说法中,正确的是( )
A.等弦所对的弧相等
B.等弧所对的弦相等
C.圆心角相等,所对的弦相等
D.弦相等,所对的圆心角相等
3 在⊙O中,圆心角∠AOB=2∠COD,则AB与CD的关系是( )
A. AB=2CD B. AB>2CD
C. AB< 2CD D. 不能确定
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
B
A
小试牛刀
4 如图,AB,CD是⊙O的两条弦 .
(1)如果AB=CD,那么________, _______________ .
(2)如果AB=CD,那么________, _______________ .
(3)如果∠AOB=∠COD,那么________, _________ .
(4)如果AB=CD,OE⊥AB,OF⊥CD,垂足分别为E,F,OE与
OF相等吗?为什么?
⌒
⌒
∠AOB=∠COD
AB=CD
∠AOB=∠COD
AB=CD
解:OE=OF,理由如下:
∵AB=CD,∴易证△ABO≌△CDO .
∴可证Rt△AOE≌Rt△COF,∴可得OE=OF .
小试牛刀
如图,在⊙O中,AB=AC,∠ACB=60°. 求证:∠AOB=∠BOC=
∠AOC .
⌒
⌒
证明:∵AB=AC,
∴AB=AC,△ABC是等腰三角形 .
又∠ACB=60°,
∴△ABC是等边三角形,AB=BC=CA .
∴∠AOB=∠BOC=∠AOC .
⌒
⌒
课堂小结
课堂小结
同一圆中证明两弦相等的“四种方法”:
(1)若两弦位于两个不同的三角形中,证明两弦所在的三角形全等.
(2)若两弦位于同一个三角形中,根据等角对等边证明两弦相等.
(3)在同一圆中证明两弦所对的弧相等(同一类弧).
(4)证明两弦所对的圆心角相等.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
