冀教版(新)九上-28.4 垂径定理【优质课件】
文档属性
| 名称 | 冀教版(新)九上-28.4 垂径定理【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:47 | ||
图片预览






文档简介
(共28张PPT)
28.4 垂径定理
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
导入新知
如图,1 400多年前,我国隋代建造的赵州石拱
桥主桥拱是圆弧形,
它的跨度(弧所对的
弦长)是 37 m,拱高
(弧的中点到弦的距
离)为 7.23 m,求赵
州桥主桥拱的半径
(精确到 0.1 m).
新课精讲
探索新知
1
知识点
垂径定理
按下面的步骤做一做:
第一步,在一张纸上任意画一个⊙O,沿圆周将圆剪下,把这个圆对折,使圆的两半部分重合;
第二步,得到一条折痕CD;
第三步,在⊙O上任取一点A,过点A作CD折痕的垂线,得到新的折痕,其中点M是两条折痕的交点,即垂足;
探索新知
总结
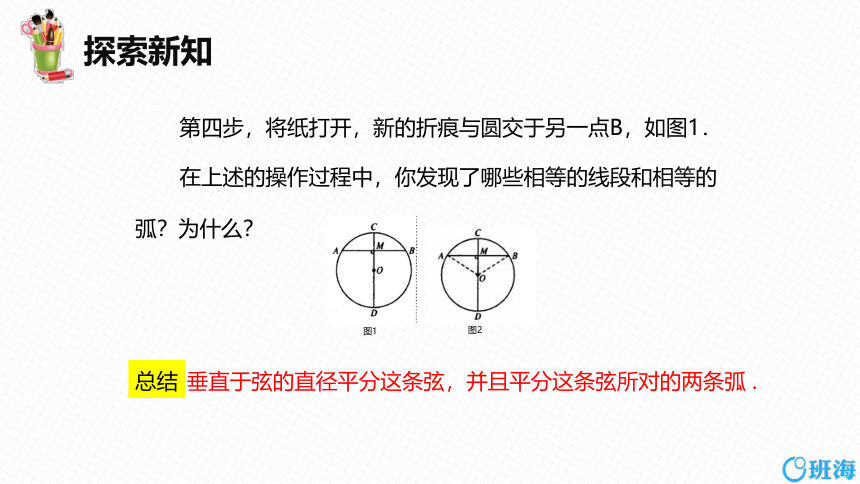
第四步,将纸打开,新的折痕与圆交于另一点B,如图1.
在上述的操作过程中,你发现了哪些相等的线段和相等的弧?为什么?
图1
图2
垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧 .
探索新知
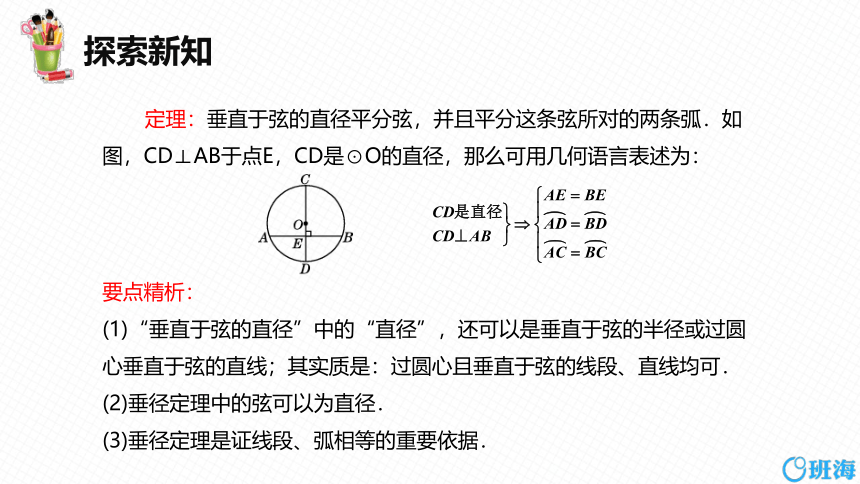
定理:垂直于弦的直径平分弦,并且平分这条弦所对的两条弧.如图,CD⊥AB于点E,CD是⊙O的直径,那么可用几何语言表述为:
要点精析:
(1)“垂直于弦的直径”中的“直径”,还可以是垂直于弦的半径或过圆心垂直于弦的直线;其实质是:过圆心且垂直于弦的线段、直线均可.
(2)垂径定理中的弦可以为直径.
(3)垂径定理是证线段、弧相等的重要依据.
探索新知
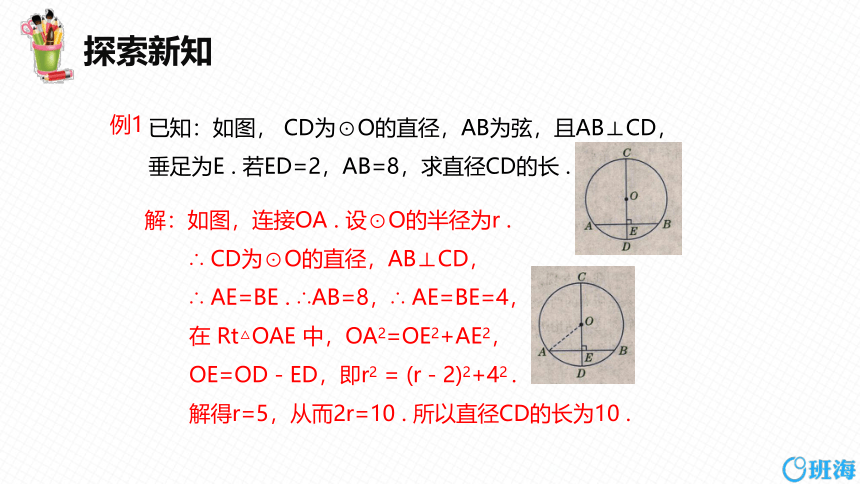
已知:如图, CD为⊙O的直径,AB为弦,且AB⊥CD,垂足为E . 若ED=2,AB=8,求直径CD的长 .
例1
解:如图,连接OA . 设⊙O的半径为r .
∴ CD为⊙O的直径,AB⊥CD,
∴ AE=BE . ∴AB=8,∴ AE=BE=4,
在 Rt△OAE 中,OA2=OE2+AE2,
OE=OD-ED,即r2 = (r-2)2+42 .
解得r=5,从而2r=10 . 所以直径CD的长为10 .
探索新知
总 结
利用垂径定理求线段长,一般是求弦长或半径或弦心距,通用的方法就是在半径、弦长的一半及弦心距三者构成的直角三角形中利用勾股定理求其中的未知的线段长.
如图,在⊙O中,OC垂直于弦AB于点C,AB=4,OC=1,则OB的长是( )
A.
B.
C.
D.
典题精讲
B
典题精讲
如图,已知⊙O的直径AB⊥CD于点E,则下列错误的是( )
A.CE=DE
B.AE=OE
C.
D.△OCE≌△ODE
如图,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON等于( )
A.5 B.7
C.9 D.11
B
A
探索新知
2
知识点
垂径定理的推论
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,如图,CD是⊙O的直径,AB是弦(非直径),AB与CD相交于点E,且AE=BE,那么可用几何语言表述为:
探索新知
例2 如图,AB,CD是⊙O的弦,M,N分别为AB,CD的中点,且∠AMN=∠CNM . 求证:AB=CD .
证明:如图,连接OM,ON,OA,OC .
∵M,N分别为AB,CD的中点,
∴AB=2AM,CD=2CN .
∴OM⊥AB,ON⊥CD . ∴∠OMA=∠ONC=90°.
∵∠AMN=∠CNM, ∴∠OMN=∠ONM . ∴OM=ON .
又∵OA=OC,∴Rt△OAM≌Rt△OCN . ∴AM=CN . ∴AB=CD .
探索新知
证明两条弦相等,可以先证明弦的一半相等.根据垂径定理的推论,连接圆心和弦的中点是常见的作辅助线的方法.
总 结
典题精讲
如图所示,⊙O的直径CD=10 cm,AB是⊙O的弦,AM=BM,OM︰OC=3︰5,则AB的长为( )
A.8 cm B. cm
C.6 cm D.2 cm
如图,△ABC的三个顶点都在⊙O上,∠AOB=60°,AB=AC=2,
则弦BC的长为( )
A. B.3
C.2 D.4
A
C
学以致用
小试牛刀
1 . 如图1,如果AB为⊙O的直径,弦CD⊥AB,垂足为E,那么下列结
论中,错误的是( )
A.CE=DE B.
C.∠BAC=∠BAD D.AC>AD
2.如图2,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则
弦AB的长是( )
A.4 B.6 C.7 D.8
D
D
小试牛刀
3.如图3,在⊙O中,P是弦AB的中点,CD是过点P的直径,则下
列结论中不正确的是( )
A.AB⊥CD B.∠AOB=4∠ACD
C. D.PO=PD
4.如图4,AB为⊙O直径,E是 中点,OE交BC于点D,BD=3,
AB=10,则AC=_____.
D
8
小试牛刀
5.P为⊙O内一点,OP=3cm,⊙O半径为5cm,则经过P点的最短
弦长为____;最长弦长为_____.
6.如图5,OE、OF分别为⊙O的弦AB、CD的弦心距,如果OE=OF,
那么__________(只需写一个正确的结论)
8
10
AB=CD
小试牛刀
7.如图所示,在平面直角坐标系中,点A的坐标是(10,0),
点B的坐标是(8,0),点C,D在以OA为直径的半圆M上,
且四边形OCDB是平行四边形,求点C的坐标.
解:如图,连接CM,作MN⊥CD于N,CH⊥OA于H .
∵四边形OCDB为平行四边形,B点的坐标是(8,0),
∴CD=OB=8,CN=MH,CH=MN .
又∵MN⊥CD,∴CN=DN= CD=4 .
易知OA=10,∴MO=MC=5 .
在Rt△MNC中,MN=
∴CH=3,又OH=OM-MH=5-4=1 . ∴点C的坐标为(1,3).
小试牛刀
8.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足
为E,BC=2 .
(1)求AB的长;
解:连接AC,
∵CD为⊙的直径,CD⊥AB,
∴AF=BF,∴AC=BC . 延长AO交⊙O于G,
则AG为⊙O的直径,又AO⊥BC,
∴BE=CE,∴AC=AB . ∴AB=BC=2 .
小试牛刀
解:由(1)知AB=BC=AC,
∴△ABC为等边三角形,
∵AE⊥BC,∴∠EAB=∠CAE= ∠CAB=30°.
即∠OAF=30°,
在Rt△OAF中,AF= ,
易得OA=2,即⊙O的半径为2 .
8.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足
为E,BC=2 .
(2)求⊙O的半径.
小试牛刀
9.某地有一座拱桥,它的桥拱是圆弧形,桥下的水面宽度为7.2米,拱顶高出水面2.4米,现有一艘宽3米,船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?
在Rt△AOD中,OA2=AD2+OD2,即r2=3.62+(r-2.4)2,解得r=3.9 .
在Rt△OHN中,OH= =3.6(米).
所以FN=DH=OH-OD=3.6-(3.9-2.4)=2.1(米).
因为2.1米>2米,所以此货船能顺利通过这座拱桥 .
解:如图,设圆弧形桥拱AB所在圆的圆心为O,
连接OA,OB,作OD⊥AB于点D,交⊙O于点C,交MN于点H,
由垂径定理可知,D为AB的中点.
设OA=r米,则OD=OC-DC=(r-2.4)米,AD= AB=3.6米.
课堂小结
课堂小结
垂径定理基本图形计算中的四变量、两关系:
(1)四变量:如图,弦长为a,圆心到弦的距离(弦心距)为d,半径为r,弧的中点到弦的距离(弓形高)为h,这四个变量中知任意两个可求其他两个.
(2)两关系:① +d2=r2;②h+d=r .
注意:计算时常作半径或过圆心作弦的垂线段来构造直角三角形 .
课堂小结
推论:平分弦(不是直径)的直径垂直于弦,并且平
分弦所对的两条弧,如图,CD是⊙O的直径,AB
是弦(非直径),AB与CD相交于点E,且AE=BE,
那么可用几何语言表述为:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
28.4 垂径定理
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
导入新知
如图,1 400多年前,我国隋代建造的赵州石拱
桥主桥拱是圆弧形,
它的跨度(弧所对的
弦长)是 37 m,拱高
(弧的中点到弦的距
离)为 7.23 m,求赵
州桥主桥拱的半径
(精确到 0.1 m).
新课精讲
探索新知
1
知识点
垂径定理
按下面的步骤做一做:
第一步,在一张纸上任意画一个⊙O,沿圆周将圆剪下,把这个圆对折,使圆的两半部分重合;
第二步,得到一条折痕CD;
第三步,在⊙O上任取一点A,过点A作CD折痕的垂线,得到新的折痕,其中点M是两条折痕的交点,即垂足;
探索新知
总结
第四步,将纸打开,新的折痕与圆交于另一点B,如图1.
在上述的操作过程中,你发现了哪些相等的线段和相等的弧?为什么?
图1
图2
垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧 .
探索新知
定理:垂直于弦的直径平分弦,并且平分这条弦所对的两条弧.如图,CD⊥AB于点E,CD是⊙O的直径,那么可用几何语言表述为:
要点精析:
(1)“垂直于弦的直径”中的“直径”,还可以是垂直于弦的半径或过圆心垂直于弦的直线;其实质是:过圆心且垂直于弦的线段、直线均可.
(2)垂径定理中的弦可以为直径.
(3)垂径定理是证线段、弧相等的重要依据.
探索新知
已知:如图, CD为⊙O的直径,AB为弦,且AB⊥CD,垂足为E . 若ED=2,AB=8,求直径CD的长 .
例1
解:如图,连接OA . 设⊙O的半径为r .
∴ CD为⊙O的直径,AB⊥CD,
∴ AE=BE . ∴AB=8,∴ AE=BE=4,
在 Rt△OAE 中,OA2=OE2+AE2,
OE=OD-ED,即r2 = (r-2)2+42 .
解得r=5,从而2r=10 . 所以直径CD的长为10 .
探索新知
总 结
利用垂径定理求线段长,一般是求弦长或半径或弦心距,通用的方法就是在半径、弦长的一半及弦心距三者构成的直角三角形中利用勾股定理求其中的未知的线段长.
如图,在⊙O中,OC垂直于弦AB于点C,AB=4,OC=1,则OB的长是( )
A.
B.
C.
D.
典题精讲
B
典题精讲
如图,已知⊙O的直径AB⊥CD于点E,则下列错误的是( )
A.CE=DE
B.AE=OE
C.
D.△OCE≌△ODE
如图,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON等于( )
A.5 B.7
C.9 D.11
B
A
探索新知
2
知识点
垂径定理的推论
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,如图,CD是⊙O的直径,AB是弦(非直径),AB与CD相交于点E,且AE=BE,那么可用几何语言表述为:
探索新知
例2 如图,AB,CD是⊙O的弦,M,N分别为AB,CD的中点,且∠AMN=∠CNM . 求证:AB=CD .
证明:如图,连接OM,ON,OA,OC .
∵M,N分别为AB,CD的中点,
∴AB=2AM,CD=2CN .
∴OM⊥AB,ON⊥CD . ∴∠OMA=∠ONC=90°.
∵∠AMN=∠CNM, ∴∠OMN=∠ONM . ∴OM=ON .
又∵OA=OC,∴Rt△OAM≌Rt△OCN . ∴AM=CN . ∴AB=CD .
探索新知
证明两条弦相等,可以先证明弦的一半相等.根据垂径定理的推论,连接圆心和弦的中点是常见的作辅助线的方法.
总 结
典题精讲
如图所示,⊙O的直径CD=10 cm,AB是⊙O的弦,AM=BM,OM︰OC=3︰5,则AB的长为( )
A.8 cm B. cm
C.6 cm D.2 cm
如图,△ABC的三个顶点都在⊙O上,∠AOB=60°,AB=AC=2,
则弦BC的长为( )
A. B.3
C.2 D.4
A
C
学以致用
小试牛刀
1 . 如图1,如果AB为⊙O的直径,弦CD⊥AB,垂足为E,那么下列结
论中,错误的是( )
A.CE=DE B.
C.∠BAC=∠BAD D.AC>AD
2.如图2,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则
弦AB的长是( )
A.4 B.6 C.7 D.8
D
D
小试牛刀
3.如图3,在⊙O中,P是弦AB的中点,CD是过点P的直径,则下
列结论中不正确的是( )
A.AB⊥CD B.∠AOB=4∠ACD
C. D.PO=PD
4.如图4,AB为⊙O直径,E是 中点,OE交BC于点D,BD=3,
AB=10,则AC=_____.
D
8
小试牛刀
5.P为⊙O内一点,OP=3cm,⊙O半径为5cm,则经过P点的最短
弦长为____;最长弦长为_____.
6.如图5,OE、OF分别为⊙O的弦AB、CD的弦心距,如果OE=OF,
那么__________(只需写一个正确的结论)
8
10
AB=CD
小试牛刀
7.如图所示,在平面直角坐标系中,点A的坐标是(10,0),
点B的坐标是(8,0),点C,D在以OA为直径的半圆M上,
且四边形OCDB是平行四边形,求点C的坐标.
解:如图,连接CM,作MN⊥CD于N,CH⊥OA于H .
∵四边形OCDB为平行四边形,B点的坐标是(8,0),
∴CD=OB=8,CN=MH,CH=MN .
又∵MN⊥CD,∴CN=DN= CD=4 .
易知OA=10,∴MO=MC=5 .
在Rt△MNC中,MN=
∴CH=3,又OH=OM-MH=5-4=1 . ∴点C的坐标为(1,3).
小试牛刀
8.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足
为E,BC=2 .
(1)求AB的长;
解:连接AC,
∵CD为⊙的直径,CD⊥AB,
∴AF=BF,∴AC=BC . 延长AO交⊙O于G,
则AG为⊙O的直径,又AO⊥BC,
∴BE=CE,∴AC=AB . ∴AB=BC=2 .
小试牛刀
解:由(1)知AB=BC=AC,
∴△ABC为等边三角形,
∵AE⊥BC,∴∠EAB=∠CAE= ∠CAB=30°.
即∠OAF=30°,
在Rt△OAF中,AF= ,
易得OA=2,即⊙O的半径为2 .
8.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足
为E,BC=2 .
(2)求⊙O的半径.
小试牛刀
9.某地有一座拱桥,它的桥拱是圆弧形,桥下的水面宽度为7.2米,拱顶高出水面2.4米,现有一艘宽3米,船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?
在Rt△AOD中,OA2=AD2+OD2,即r2=3.62+(r-2.4)2,解得r=3.9 .
在Rt△OHN中,OH= =3.6(米).
所以FN=DH=OH-OD=3.6-(3.9-2.4)=2.1(米).
因为2.1米>2米,所以此货船能顺利通过这座拱桥 .
解:如图,设圆弧形桥拱AB所在圆的圆心为O,
连接OA,OB,作OD⊥AB于点D,交⊙O于点C,交MN于点H,
由垂径定理可知,D为AB的中点.
设OA=r米,则OD=OC-DC=(r-2.4)米,AD= AB=3.6米.
课堂小结
课堂小结
垂径定理基本图形计算中的四变量、两关系:
(1)四变量:如图,弦长为a,圆心到弦的距离(弦心距)为d,半径为r,弧的中点到弦的距离(弓形高)为h,这四个变量中知任意两个可求其他两个.
(2)两关系:① +d2=r2;②h+d=r .
注意:计算时常作半径或过圆心作弦的垂线段来构造直角三角形 .
课堂小结
推论:平分弦(不是直径)的直径垂直于弦,并且平
分弦所对的两条弧,如图,CD是⊙O的直径,AB
是弦(非直径),AB与CD相交于点E,且AE=BE,
那么可用几何语言表述为:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
