冀教版(新)九上-28.5 弧长和扇形面积的计算 第二课时【优质课件】
文档属性
| 名称 | 冀教版(新)九上-28.5 弧长和扇形面积的计算 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:47 | ||
图片预览








文档简介
(共24张PPT)
28.5 弧长和扇形面积的计算
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.大家见过圆锥吗?你能举出实例吗?
2.根据你以前的所学,说说你对圆锥的一些认识。
3.圆锥的曲面展开图是什么形状呢?应怎样计算它的面积呢?
新课精讲
探索新知
1
知识点
圆锥及其侧面展开图相关量的计算
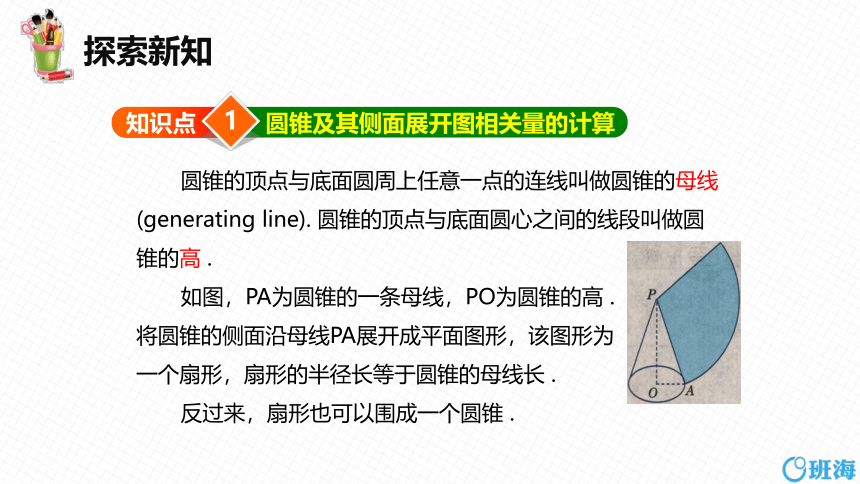
圆锥的顶点与底面圆周上任意一点的连线叫做圆锥的母线(generating line). 圆锥的顶点与底面圆心之间的线段叫做圆锥的高 .
如图,PA为圆锥的一条母线,PO为圆锥的高 .
将圆锥的侧面沿母线PA展开成平面图形,该图形为
一个扇形,扇形的半径长等于圆锥的母线长 .
反过来,扇形也可以围成一个圆锥 .
探索新知
1.圆锥:圆锥是由一个底面和一个侧面围成的几何体.如图所示.
2.圆锥的母线:如图所示,圆锥的顶点与底面圆周上任意一点的连线叫做圆锥的母线.母线有无数条,且每条母线都相等.
3.圆锥的高:如图所示,圆锥的顶点与底面圆心之间的线段叫做圆锥的高.
探索新知
若用一张直径为20 cm的半圆形铁片做一个圆锥的侧面,接缝忽略不计,则所得圆锥的高为( )
A.5 cm B.5 cm
C. cm D.10 cm
例1
A
导引:根据侧面展开图的弧长等于圆锥底面的圆周长,得到圆锥底面的半径,再利用勾股定理计算圆锥的高.依题意,得 ×20π=2πr,解得r=5,由勾股定理,得所得圆锥的高为=5(cm),故应选A .
探索新知
结 论
圆锥的侧面展开图的弧长等于底面的圆周长,
圆锥的母线l、圆锥的底面半径r、圆锥的高h,三
者满足r2+h2=l2 .
如图,圆心角∠AOB=20°,将 旋转n°得到 ,则 的度
数是_____°.
典题精讲
2 已知一个圆锥的高为6cm,半径为8cm,则这个圆锥的母长
为_______.
20
10cm
典题精讲
2 已知圆锥的母线长是12,它的侧面展开图的圆心角是120°,则它的底面圆的直径为( )
A.2 B.4 C.6 D.8
3 圆锥的侧面展开图是一个弧长为12π的扇形,则这个圆锥底面圆的半径是( )
A.24 B.12 C.6 D.3
D
C
探索新知
2
知识点
圆锥的侧面积和全面积
1.圆锥的有关计算公式:
(1)圆锥的高h,底面半径r,母线l的关系式:h2+r2=l2(已知其中任意两个量,可以求出第三个量).
(2)圆锥侧面积公式S侧=πrl.
(3)圆锥全面积公式S全=πrl+πr2.
2.易错警示:圆锥的母线长为圆锥侧面展开后所得扇形的半径,要注意与圆锥底面半径相区分.
3.经过圆锥的高的平面截圆锥所得的图形是等腰三角形.
探索新知
例2 如图,用一张半径为24 cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计),如果圆锥形帽子的底面半径为10 cm,那么这张扇形纸板的面积是( )
A.240π cm2 B.480π cm2
C.1 200π cm2 D.2 400π cm2
导引:圆锥的侧面展开图是扇形,圆锥的侧面积就是相关扇形的面积,直接利用圆锥的侧面积公式S=πrl计算.S=πrl=π×10×24=240π(cm2),故选择A .
A
探索新知
对于圆锥的计算考查主要有三种形式:
(1)圆锥的底面半径、高、母线长中已知两个求圆锥的侧面积或全面积;
(2)知道圆锥的侧面积和底面半径,求母线长或高或圆锥侧面展开图的圆心角;
(3)已知圆锥侧面展开图弧长及圆心角度数,求圆锥的底面半径和高.
总 结
典题精讲
如图是某工件的三视图,则此工件的表面积为( )
A.15π cm2 B.51π cm2
C.66π cm2 D.24π cm2
已知一个圆锥的底面半径为12 cm,母线长为20cm,则这个圆
锥的侧面积为________.
D
240π
学以致用
1 . 若一个圆锥的侧面展开图是半径为18 cm,圆心角为240°的扇形,则这个圆锥的底面半径是( )
A.6 cm B.9 cm C.12 cm D.18 cm
小试牛刀
C
2. 如图,圆锥的底面半径r为 6 cm,高h为8 cm,则圆锥的侧面
积为( )
A.30π cm
B.48π cm
C.60π cm
D.80π cm
C
小试牛刀
3 圆锥的侧面展开图是一个弧长为12π的扇形,则这个圆锥底面圆的半径是( )
A.24 B.12 C.6 D.3
4 如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4∶5,那么需要扇形铁皮的圆心角应为( )
A.288° B.144° C.216° D.120°
5 如图,从一块直径是8 m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )m.
A.4 B.5 C. D.2
C
A
C
小试牛刀
6.沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥底面
圆的半径r=2 cm,扇形的圆心角θ=120°,则该圆锥的母线长l
为____cm.
6
7.已知圆锥的底面直径为20 cm,母线长为90 cm,则圆锥的表面
积是________ cm . (结果保留π)
1000π
8.粮仓顶部是一个圆锥形,其底面周长为36 m,母线长为8 m,为
防雨需在粮仓顶部铺上油毡,如果按用料的10%计接头的重合部
分,那么这座粮仓实际需用______m2的油毡.
160
小试牛刀
7. 一个圆锥形烟囱帽的底面直径是40 cm,母线长是120 cm,加工
这样的一个烟囱帽,至少需要多少铁皮(不计接头)
8.已知扇形的圆心角为120°,面积为300π cm2. 求扇形的弧长;
解:侧面积为: ×40π×120=2 400π(cm2).
小试牛刀
9 . 蒙古包可以近似地看作由圆锥和圆柱组成 . 如果想用毛毡搭建20个底面积为12 m2,高为3.2 m,外围高1.8 m的蒙古包,至少需要多少平方米的毛毡 (π取3.142,结果取整数)?
解:如图是一个蒙古包的示意图 .
根据题意,下部圆柱的底面积为12 m2,
高h2=1.8 m;上部圆锥的高h1=3.2-1.8=1.4(m).
圆柱的底面圆的半径r = 侧面积为2π×1.954×1.8≈22.10 (m2).
h1
h2
r
圆锥的母线长l=
侧面展开扇形的弧长为2π×1.954≈12.28(m),
圆锥的侧面积为 ×2.404×12.28≈14.76(m2).
因此,搭建20个这样的蒙古包至少需要毛毡20×(22.10+14.76)≈738(m2).
课堂小结
课堂小结
1.圆锥和侧面展开图之间转换的“两个对应”:
(1)圆锥的母线与展开后扇形的半径的对应.
(2)展开后扇形的弧长与圆锥底面圆周长的对应.
2.圆锥面积计算的“三个关键点”:
(1)分析清楚几何体表面的构成.
(2)弄清圆锥与其侧面展开后扇形各元素之间的对应关系.
(3)圆锥的母线长l,底面圆的半径r和圆锥的高h的关系为:l2=r2+h2.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
28.5 弧长和扇形面积的计算
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.大家见过圆锥吗?你能举出实例吗?
2.根据你以前的所学,说说你对圆锥的一些认识。
3.圆锥的曲面展开图是什么形状呢?应怎样计算它的面积呢?
新课精讲
探索新知
1
知识点
圆锥及其侧面展开图相关量的计算
圆锥的顶点与底面圆周上任意一点的连线叫做圆锥的母线(generating line). 圆锥的顶点与底面圆心之间的线段叫做圆锥的高 .
如图,PA为圆锥的一条母线,PO为圆锥的高 .
将圆锥的侧面沿母线PA展开成平面图形,该图形为
一个扇形,扇形的半径长等于圆锥的母线长 .
反过来,扇形也可以围成一个圆锥 .
探索新知
1.圆锥:圆锥是由一个底面和一个侧面围成的几何体.如图所示.
2.圆锥的母线:如图所示,圆锥的顶点与底面圆周上任意一点的连线叫做圆锥的母线.母线有无数条,且每条母线都相等.
3.圆锥的高:如图所示,圆锥的顶点与底面圆心之间的线段叫做圆锥的高.
探索新知
若用一张直径为20 cm的半圆形铁片做一个圆锥的侧面,接缝忽略不计,则所得圆锥的高为( )
A.5 cm B.5 cm
C. cm D.10 cm
例1
A
导引:根据侧面展开图的弧长等于圆锥底面的圆周长,得到圆锥底面的半径,再利用勾股定理计算圆锥的高.依题意,得 ×20π=2πr,解得r=5,由勾股定理,得所得圆锥的高为=5(cm),故应选A .
探索新知
结 论
圆锥的侧面展开图的弧长等于底面的圆周长,
圆锥的母线l、圆锥的底面半径r、圆锥的高h,三
者满足r2+h2=l2 .
如图,圆心角∠AOB=20°,将 旋转n°得到 ,则 的度
数是_____°.
典题精讲
2 已知一个圆锥的高为6cm,半径为8cm,则这个圆锥的母长
为_______.
20
10cm
典题精讲
2 已知圆锥的母线长是12,它的侧面展开图的圆心角是120°,则它的底面圆的直径为( )
A.2 B.4 C.6 D.8
3 圆锥的侧面展开图是一个弧长为12π的扇形,则这个圆锥底面圆的半径是( )
A.24 B.12 C.6 D.3
D
C
探索新知
2
知识点
圆锥的侧面积和全面积
1.圆锥的有关计算公式:
(1)圆锥的高h,底面半径r,母线l的关系式:h2+r2=l2(已知其中任意两个量,可以求出第三个量).
(2)圆锥侧面积公式S侧=πrl.
(3)圆锥全面积公式S全=πrl+πr2.
2.易错警示:圆锥的母线长为圆锥侧面展开后所得扇形的半径,要注意与圆锥底面半径相区分.
3.经过圆锥的高的平面截圆锥所得的图形是等腰三角形.
探索新知
例2 如图,用一张半径为24 cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计),如果圆锥形帽子的底面半径为10 cm,那么这张扇形纸板的面积是( )
A.240π cm2 B.480π cm2
C.1 200π cm2 D.2 400π cm2
导引:圆锥的侧面展开图是扇形,圆锥的侧面积就是相关扇形的面积,直接利用圆锥的侧面积公式S=πrl计算.S=πrl=π×10×24=240π(cm2),故选择A .
A
探索新知
对于圆锥的计算考查主要有三种形式:
(1)圆锥的底面半径、高、母线长中已知两个求圆锥的侧面积或全面积;
(2)知道圆锥的侧面积和底面半径,求母线长或高或圆锥侧面展开图的圆心角;
(3)已知圆锥侧面展开图弧长及圆心角度数,求圆锥的底面半径和高.
总 结
典题精讲
如图是某工件的三视图,则此工件的表面积为( )
A.15π cm2 B.51π cm2
C.66π cm2 D.24π cm2
已知一个圆锥的底面半径为12 cm,母线长为20cm,则这个圆
锥的侧面积为________.
D
240π
学以致用
1 . 若一个圆锥的侧面展开图是半径为18 cm,圆心角为240°的扇形,则这个圆锥的底面半径是( )
A.6 cm B.9 cm C.12 cm D.18 cm
小试牛刀
C
2. 如图,圆锥的底面半径r为 6 cm,高h为8 cm,则圆锥的侧面
积为( )
A.30π cm
B.48π cm
C.60π cm
D.80π cm
C
小试牛刀
3 圆锥的侧面展开图是一个弧长为12π的扇形,则这个圆锥底面圆的半径是( )
A.24 B.12 C.6 D.3
4 如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4∶5,那么需要扇形铁皮的圆心角应为( )
A.288° B.144° C.216° D.120°
5 如图,从一块直径是8 m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )m.
A.4 B.5 C. D.2
C
A
C
小试牛刀
6.沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥底面
圆的半径r=2 cm,扇形的圆心角θ=120°,则该圆锥的母线长l
为____cm.
6
7.已知圆锥的底面直径为20 cm,母线长为90 cm,则圆锥的表面
积是________ cm . (结果保留π)
1000π
8.粮仓顶部是一个圆锥形,其底面周长为36 m,母线长为8 m,为
防雨需在粮仓顶部铺上油毡,如果按用料的10%计接头的重合部
分,那么这座粮仓实际需用______m2的油毡.
160
小试牛刀
7. 一个圆锥形烟囱帽的底面直径是40 cm,母线长是120 cm,加工
这样的一个烟囱帽,至少需要多少铁皮(不计接头)
8.已知扇形的圆心角为120°,面积为300π cm2. 求扇形的弧长;
解:侧面积为: ×40π×120=2 400π(cm2).
小试牛刀
9 . 蒙古包可以近似地看作由圆锥和圆柱组成 . 如果想用毛毡搭建20个底面积为12 m2,高为3.2 m,外围高1.8 m的蒙古包,至少需要多少平方米的毛毡 (π取3.142,结果取整数)?
解:如图是一个蒙古包的示意图 .
根据题意,下部圆柱的底面积为12 m2,
高h2=1.8 m;上部圆锥的高h1=3.2-1.8=1.4(m).
圆柱的底面圆的半径r = 侧面积为2π×1.954×1.8≈22.10 (m2).
h1
h2
r
圆锥的母线长l=
侧面展开扇形的弧长为2π×1.954≈12.28(m),
圆锥的侧面积为 ×2.404×12.28≈14.76(m2).
因此,搭建20个这样的蒙古包至少需要毛毡20×(22.10+14.76)≈738(m2).
课堂小结
课堂小结
1.圆锥和侧面展开图之间转换的“两个对应”:
(1)圆锥的母线与展开后扇形的半径的对应.
(2)展开后扇形的弧长与圆锥底面圆周长的对应.
2.圆锥面积计算的“三个关键点”:
(1)分析清楚几何体表面的构成.
(2)弄清圆锥与其侧面展开后扇形各元素之间的对应关系.
(3)圆锥的母线长l,底面圆的半径r和圆锥的高h的关系为:l2=r2+h2.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
