冀教版(新)九上-28.5 弧长和扇形面积的计算 第一课时【优质课件】
文档属性
| 名称 | 冀教版(新)九上-28.5 弧长和扇形面积的计算 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
28.5 弧长和扇形面积的计算
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
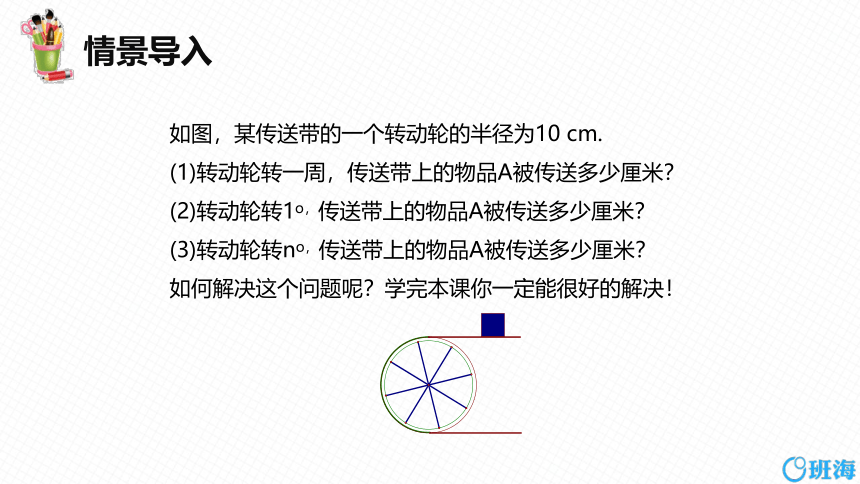
如图,某传送带的一个转动轮的半径为10 cm.
(1)转动轮转一周,传送带上的物品A被传送多少厘米?
(2)转动轮转1o,传送带上的物品A被传送多少厘米?
(3)转动轮转no,传送带上的物品A被传送多少厘米?
如何解决这个问题呢?学完本课你一定能很好的解决!
新课精讲
探索新知
1
知识点
弧长公式
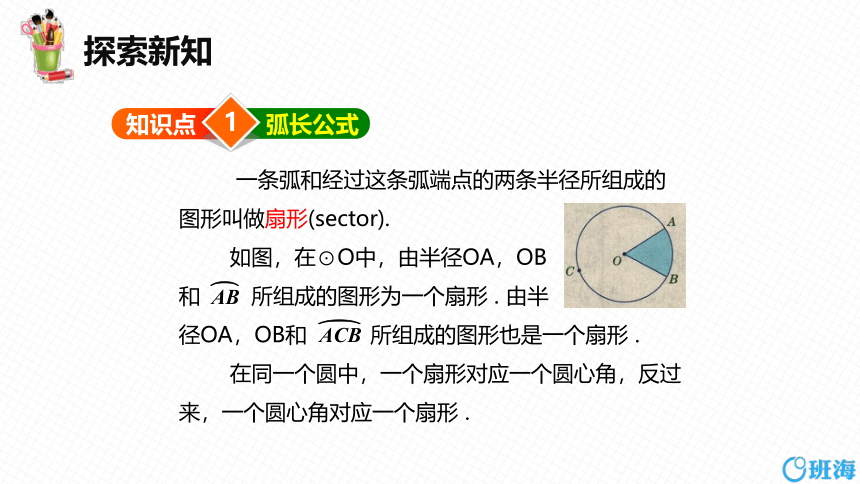
一条弧和经过这条弧端点的两条半径所组成的图形叫做扇形(sector).
如图,在⊙O中,由半径OA,OB
和 所组成的图形为一个扇形 . 由半
径OA,OB和 所组成的图形也是一个扇形 .
在同一个圆中,一个扇形对应一个圆心角,反过来,一个圆心角对应一个扇形 .
探索新知
半径为r的⊙O,它的周长为2πr,圆心角为360°. 按下表的圆心角,计算所对的弧长以及扇形的面积,填写下表:
探究:
给定的圆心角 1° 90° n°
所对的弧长
1°圆心角所对弧的长为
总结:
若设n°圆心角所对弧的长为l,
探索新知
如图,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600米,E为弧CD上一点,且OE⊥CD,垂足为F,
OF=300 米,则这段弯路的长度为( )
A.200π米 B.100π米
C.400π米 D.300π米
例1
A
导引:设这段弯路的半径为R米.∵OE⊥CD,∴CF= CD= ×600=300(米).
根据勾股定理,得OC2=CF2+OF2,即R2=3002+(300 )2 .
解得R=600 . ∴∠COF=30°. ∴∠COD=60°.
∴这段弯路的长度为 =200π(米) .
探索新知
总 结
求弧长需要两个条件:
(1)弧所在圆的半径;
(2)弧所对的圆心角.当题中没有直接给出这两个条件时,则需利用圆的相关知识:弦、弦心距、圆周角等求出圆的半径或弧所对的圆心角.
典题精讲
1 已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为( )
A. B.2π C.3π D.12π
在半径为6的⊙O中,60°圆心角所对的弧长是( )
A.π B.2π C.4π D.6π
C
B
典题精讲
如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则 的长为( )
A. π B. π
C. π D. π
B
探索新知
2
知识点
扇形面积公式
半径为r的⊙O,面积为πr2,圆心角为360°. 按下表的圆心角,计算所对的弧长以及扇形的面积,填写下表:
给定的圆心角 1° 90° n°
扇形面积
1°圆心角所扇形的面积为 若设n°圆心角所对
扇形的面积为S,则
这就是计算扇形面积的公式 . 因为
所以扇形的面积公式还可以表示为
探索新知
扇形面积公式:
S扇形= ;S扇形= lr (l是扇形的弧长).
应用方法:①当已知半径r和圆心角的度数n°求扇形的面积时,选用公式S扇形= ;
②当已知半径r和弧长l求扇形的面积时,选用公式S扇形= lr.
特别注意:①已知S扇形,l,n,r四个量中的任意两个量,可以求出另外两个量.
②在扇形面积公式 S扇形= 中,n,360不带单位 .
探索新知
例2 如图,⊙O的半径为10 cm .
(1)如果∠AOB=100°,求 的长及扇形AOB的面积 . (结果保留一位小数)
(2)已知 =25 cm,求∠BOC的度数 . (结果精确到1°)
探索新知
解:(1) r=10 cm,∠AOB=100°,由弧长和扇形面积公式,得
所以 的长约为17. 4 cm,扇形AOB的面积约为87. 2 cm2 .
(2)r=10 cm, =25 cm,由弧长公式,得
所以∠BOC约为143° .
探索新知
扇形的面积公式有两个,若已知圆心角的度数和
半径,则用S扇形= ;若已知扇形的弧长和半径,
则用S扇形= lR(l是扇形的弧长).
总 结
若扇形的面积为3π,圆心角为60°,则该扇形的半径为( )
A.3 B.9 C.2 D.3
如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2 时,则阴影部分的面积为( )
A.2π-4 B.4π-8
C.2π-8 D.4π-4
典题精讲
D
A
典题精讲
3 如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在 上,设∠BDF=α(0°<α<90°).当α由小到大变化时,图中阴影部分的面积( )
A.由小变大
B.由大变小
C.不变
D.先由小变大,后由大变小
C
学以致用
小试牛刀
1.一个扇形的半径为8 cm,弧长为 π cm,则扇形的圆心角为( )
A.60° B.120°
C.150° D.180°
B
2.如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=3,
OC=1,分别连接AC,BD,则图中阴影部分的面积为( )
A. π B.π
C.2π D.4π
C
小试牛刀
3. 如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为
120°,AB长为25 cm,贴纸部分的宽BD为15 cm,若纸扇两面
贴纸,则贴纸的面积为( )
A.175π cm2 B.350π cm2
C.π cm2 D.150π cm2
B
5.如果一条弧长等于R,它的半径是R,那么这条弧所对的圆心角
度数为_____,当圆心角增加30°时,这条弧长增加πR .
6.如图,点A,B,C在半径为9的⊙O上, 的长为2π,则∠ACB
的大小是_____.
小试牛刀
4.已知扇形的面积为240π,圆心角为150°,则扇形的半径R=____,
弧长l=_____ .
24
20π
45°
20°
小试牛刀
7.如图所示, 所在圆的半径为R, 的长为R,⊙O′和OA,
OB分别相切于点C,E,且与⊙O内切于点D,求⊙O′的周长.
解:如图,连接OD,O′C,则O′在OD上.
小试牛刀
8.如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=
60°,OC=2 .
(1)求OE和CD的长;
小试牛刀
8.如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=
60°,OC=2 .
(2)求圆中阴影部分的面积.
小试牛刀
9 . 如图1,水平放置的圆柱形排水管道的截面半径是0.6 m,其中水面高 0.3 m,求截面上有水部分的面积(结果保留小数点后两位).
O
图1
⌒
O
A
B
C
D
图2
解:如图2,连接OA,OB,作弦AB的垂直平分线,
垂足为D,交AB于点C,连接AC .
∵OC=0.6 m,DC=0.3 m,
∴OD=OC-DC=0.3(m). ∴OD=DC .
又AD⊥DC, ∴AD是线段OC的垂直平分线 .
∴AC=AO=OC . 从而∠AOD=60°,∠AOB=120°.
有水部分的面积
课堂小结
课堂小结
1. 弧长公式为
2. 扇形的面积计算公式为
3. 弧长和扇形面积都和圆心角n°,半径r有关系,
因此l和S之间也有一定的关系,列式表示为:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
28.5 弧长和扇形面积的计算
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图,某传送带的一个转动轮的半径为10 cm.
(1)转动轮转一周,传送带上的物品A被传送多少厘米?
(2)转动轮转1o,传送带上的物品A被传送多少厘米?
(3)转动轮转no,传送带上的物品A被传送多少厘米?
如何解决这个问题呢?学完本课你一定能很好的解决!
新课精讲
探索新知
1
知识点
弧长公式
一条弧和经过这条弧端点的两条半径所组成的图形叫做扇形(sector).
如图,在⊙O中,由半径OA,OB
和 所组成的图形为一个扇形 . 由半
径OA,OB和 所组成的图形也是一个扇形 .
在同一个圆中,一个扇形对应一个圆心角,反过来,一个圆心角对应一个扇形 .
探索新知
半径为r的⊙O,它的周长为2πr,圆心角为360°. 按下表的圆心角,计算所对的弧长以及扇形的面积,填写下表:
探究:
给定的圆心角 1° 90° n°
所对的弧长
1°圆心角所对弧的长为
总结:
若设n°圆心角所对弧的长为l,
探索新知
如图,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600米,E为弧CD上一点,且OE⊥CD,垂足为F,
OF=300 米,则这段弯路的长度为( )
A.200π米 B.100π米
C.400π米 D.300π米
例1
A
导引:设这段弯路的半径为R米.∵OE⊥CD,∴CF= CD= ×600=300(米).
根据勾股定理,得OC2=CF2+OF2,即R2=3002+(300 )2 .
解得R=600 . ∴∠COF=30°. ∴∠COD=60°.
∴这段弯路的长度为 =200π(米) .
探索新知
总 结
求弧长需要两个条件:
(1)弧所在圆的半径;
(2)弧所对的圆心角.当题中没有直接给出这两个条件时,则需利用圆的相关知识:弦、弦心距、圆周角等求出圆的半径或弧所对的圆心角.
典题精讲
1 已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为( )
A. B.2π C.3π D.12π
在半径为6的⊙O中,60°圆心角所对的弧长是( )
A.π B.2π C.4π D.6π
C
B
典题精讲
如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则 的长为( )
A. π B. π
C. π D. π
B
探索新知
2
知识点
扇形面积公式
半径为r的⊙O,面积为πr2,圆心角为360°. 按下表的圆心角,计算所对的弧长以及扇形的面积,填写下表:
给定的圆心角 1° 90° n°
扇形面积
1°圆心角所扇形的面积为 若设n°圆心角所对
扇形的面积为S,则
这就是计算扇形面积的公式 . 因为
所以扇形的面积公式还可以表示为
探索新知
扇形面积公式:
S扇形= ;S扇形= lr (l是扇形的弧长).
应用方法:①当已知半径r和圆心角的度数n°求扇形的面积时,选用公式S扇形= ;
②当已知半径r和弧长l求扇形的面积时,选用公式S扇形= lr.
特别注意:①已知S扇形,l,n,r四个量中的任意两个量,可以求出另外两个量.
②在扇形面积公式 S扇形= 中,n,360不带单位 .
探索新知
例2 如图,⊙O的半径为10 cm .
(1)如果∠AOB=100°,求 的长及扇形AOB的面积 . (结果保留一位小数)
(2)已知 =25 cm,求∠BOC的度数 . (结果精确到1°)
探索新知
解:(1) r=10 cm,∠AOB=100°,由弧长和扇形面积公式,得
所以 的长约为17. 4 cm,扇形AOB的面积约为87. 2 cm2 .
(2)r=10 cm, =25 cm,由弧长公式,得
所以∠BOC约为143° .
探索新知
扇形的面积公式有两个,若已知圆心角的度数和
半径,则用S扇形= ;若已知扇形的弧长和半径,
则用S扇形= lR(l是扇形的弧长).
总 结
若扇形的面积为3π,圆心角为60°,则该扇形的半径为( )
A.3 B.9 C.2 D.3
如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2 时,则阴影部分的面积为( )
A.2π-4 B.4π-8
C.2π-8 D.4π-4
典题精讲
D
A
典题精讲
3 如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在 上,设∠BDF=α(0°<α<90°).当α由小到大变化时,图中阴影部分的面积( )
A.由小变大
B.由大变小
C.不变
D.先由小变大,后由大变小
C
学以致用
小试牛刀
1.一个扇形的半径为8 cm,弧长为 π cm,则扇形的圆心角为( )
A.60° B.120°
C.150° D.180°
B
2.如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=3,
OC=1,分别连接AC,BD,则图中阴影部分的面积为( )
A. π B.π
C.2π D.4π
C
小试牛刀
3. 如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为
120°,AB长为25 cm,贴纸部分的宽BD为15 cm,若纸扇两面
贴纸,则贴纸的面积为( )
A.175π cm2 B.350π cm2
C.π cm2 D.150π cm2
B
5.如果一条弧长等于R,它的半径是R,那么这条弧所对的圆心角
度数为_____,当圆心角增加30°时,这条弧长增加πR .
6.如图,点A,B,C在半径为9的⊙O上, 的长为2π,则∠ACB
的大小是_____.
小试牛刀
4.已知扇形的面积为240π,圆心角为150°,则扇形的半径R=____,
弧长l=_____ .
24
20π
45°
20°
小试牛刀
7.如图所示, 所在圆的半径为R, 的长为R,⊙O′和OA,
OB分别相切于点C,E,且与⊙O内切于点D,求⊙O′的周长.
解:如图,连接OD,O′C,则O′在OD上.
小试牛刀
8.如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=
60°,OC=2 .
(1)求OE和CD的长;
小试牛刀
8.如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=
60°,OC=2 .
(2)求圆中阴影部分的面积.
小试牛刀
9 . 如图1,水平放置的圆柱形排水管道的截面半径是0.6 m,其中水面高 0.3 m,求截面上有水部分的面积(结果保留小数点后两位).
O
图1
⌒
O
A
B
C
D
图2
解:如图2,连接OA,OB,作弦AB的垂直平分线,
垂足为D,交AB于点C,连接AC .
∵OC=0.6 m,DC=0.3 m,
∴OD=OC-DC=0.3(m). ∴OD=DC .
又AD⊥DC, ∴AD是线段OC的垂直平分线 .
∴AC=AO=OC . 从而∠AOD=60°,∠AOB=120°.
有水部分的面积
课堂小结
课堂小结
1. 弧长公式为
2. 扇形的面积计算公式为
3. 弧长和扇形面积都和圆心角n°,半径r有关系,
因此l和S之间也有一定的关系,列式表示为:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
