冀教版(新)五上-第六单元 4.组合图形面积【优质课件】
文档属性
| 名称 | 冀教版(新)五上-第六单元 4.组合图形面积【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
组合图形面积
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目 录
01 课前导入
02 新课精讲
03 学以致用
04 课堂小结
01
课前导入
情景导入
长方形的面积=
平行四边形的面积=
三角形的面积=
梯形的面积=
长×宽
底×高
底×高÷2
(上底+下底)×高÷2
大家回忆一下,下面图形的面积公式是什么呢
02
新课精讲
探索新知
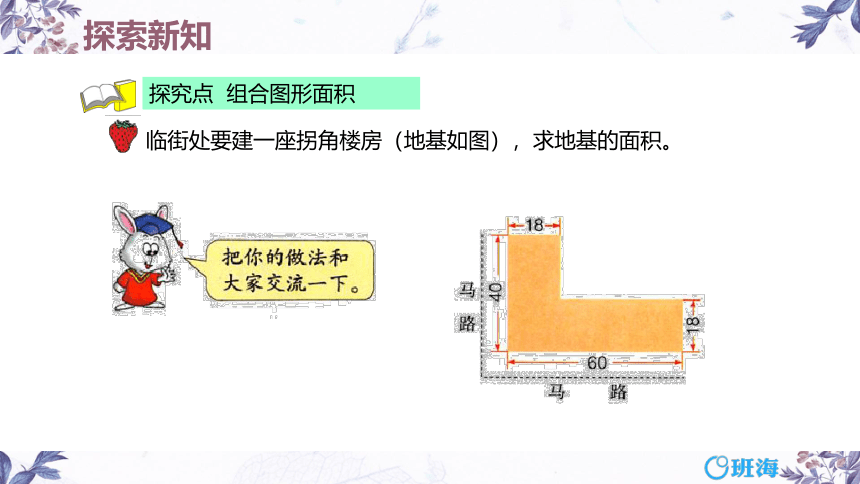
临街处要建一座拐角楼房(地基如图),求地基的面积。
探究点 组合图形面积
探索新知
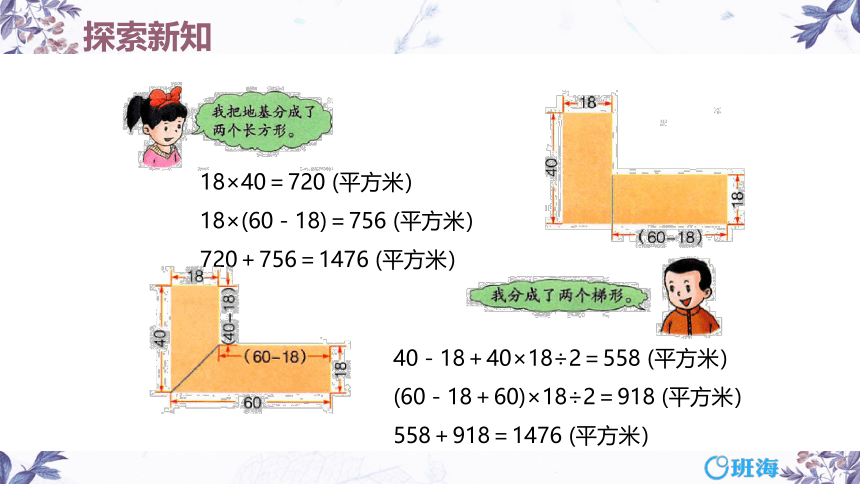
18×40=720 (平方米)
18×(60-18)=756 (平方米) 720+756=1476 (平方米)
40-18+40×18÷2=558 (平方米)
(60-18+60)×18÷2=918 (平方米) 558+918=1476 (平方米)
典题精讲
1.下面组合图形可以分成哪些已经学过的图形?请你在图中画一画。
答案不唯一。
2.用分割法计算下面图形的面积。(单位:厘米)
4×1.5÷2+4×2÷2=7(平方厘米)
(1)
典题精讲
(25-10)×(10+10)÷2+10×10
=250(平方厘米)
20×10=200(平方厘米)
20×8=160(平方厘米)
200+160=360(平方厘米)
(2)
(3)
典题精讲
3.用添补法计算组合图形的面积。(单位:厘米)
15×8-3×2=114(平方厘米)
(10+10+5)×10÷2-6×8÷2
=101(平方厘米)
(1)
(2)
4.求下面各图中阴影部分的面积。(单位:厘米)
8×6÷2+6×6÷2
=42(平方厘米)
8×8+12×12=208(平方厘米)
(8×8÷2=32(平方厘米)
(8+12)×12÷2=120(平方厘米)
(12-8)×12÷2=24(平方厘米)
208-32-120-24=32(平方厘米)
(2)
(1)
典题精讲
5.用不同的方法计算下图的面积。(单位:厘米)(用四种方法解答)
方法一:
3×4+(4+10)×(8-3)÷2=12+35=47(平方厘米)
方法二:
8×4+(8-3)×(10-4)÷2=32+15=47(平方厘米)
方法三:
8×10-(8+3)×(10-4)÷2=80-33=47(平方厘米)
方法四:
(8+3)×4÷2+(8-3)×10÷2=22+25=47(平方厘米)
典题精讲
易错提醒
数学门诊。(下面的解答对吗?不对的请改正)
一块铁板的形状如图。在这块铁板的一面涂上油漆,涂油漆的面积是多少?(单位:分米)
解答:(2+4+2)÷2=4(分米)
(8+10)×4÷2×2=72(平方分米) ( )
改正:
×
辨析:分割图形错误,分割方法没有根据。
2+4+2=8(分米) 8×8=64(平方分米)
(4+8)×(10-8)÷2=12(平方分米)
64+12=76(平方分米)
03
学以致用
小试牛刀
1. 计算下面组合图形的面积。(单位:cm)
(8+16)×(16-9)÷2=84(cm2)
16×9=144(cm2)
84+144=228(cm2)
25×15=375(cm2)
(20-15)×(25-15)÷2=25(cm2)
375+25=400(cm2)
小试牛刀
2. 一块菜地(如下图),求它的面积。(单位:m)
18×18÷2=162(m2)
(18+12)×22÷2=330(m2)
162+330=492(m2)
3. 一块梯形稻田,中间有一条水渠通过。
(1)实际种植水稻的面积是多少平方米?
(2)如果每平方米稻田产水稻1.2千克,那么这块稻田共产水稻多少千克?
934.5×1.2=1121.4(千克)
(44+48)×21÷2=966(m2) 1.5×21=31.5(m2)
966-31.5=934.5(m2)
04
课堂小结
归纳总结:
求组合图形面积的基本方法:
1.观察分析组合图形可分割或添补成哪些已经学过的基本图形。
2.找出计算基本图形面积需要的条件。
3.利用合理的方法,先计算出基本图形的面积,再计算出组合图形的面积。
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
组合图形面积
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目 录
01 课前导入
02 新课精讲
03 学以致用
04 课堂小结
01
课前导入
情景导入
长方形的面积=
平行四边形的面积=
三角形的面积=
梯形的面积=
长×宽
底×高
底×高÷2
(上底+下底)×高÷2
大家回忆一下,下面图形的面积公式是什么呢
02
新课精讲
探索新知
临街处要建一座拐角楼房(地基如图),求地基的面积。
探究点 组合图形面积
探索新知
18×40=720 (平方米)
18×(60-18)=756 (平方米) 720+756=1476 (平方米)
40-18+40×18÷2=558 (平方米)
(60-18+60)×18÷2=918 (平方米) 558+918=1476 (平方米)
典题精讲
1.下面组合图形可以分成哪些已经学过的图形?请你在图中画一画。
答案不唯一。
2.用分割法计算下面图形的面积。(单位:厘米)
4×1.5÷2+4×2÷2=7(平方厘米)
(1)
典题精讲
(25-10)×(10+10)÷2+10×10
=250(平方厘米)
20×10=200(平方厘米)
20×8=160(平方厘米)
200+160=360(平方厘米)
(2)
(3)
典题精讲
3.用添补法计算组合图形的面积。(单位:厘米)
15×8-3×2=114(平方厘米)
(10+10+5)×10÷2-6×8÷2
=101(平方厘米)
(1)
(2)
4.求下面各图中阴影部分的面积。(单位:厘米)
8×6÷2+6×6÷2
=42(平方厘米)
8×8+12×12=208(平方厘米)
(8×8÷2=32(平方厘米)
(8+12)×12÷2=120(平方厘米)
(12-8)×12÷2=24(平方厘米)
208-32-120-24=32(平方厘米)
(2)
(1)
典题精讲
5.用不同的方法计算下图的面积。(单位:厘米)(用四种方法解答)
方法一:
3×4+(4+10)×(8-3)÷2=12+35=47(平方厘米)
方法二:
8×4+(8-3)×(10-4)÷2=32+15=47(平方厘米)
方法三:
8×10-(8+3)×(10-4)÷2=80-33=47(平方厘米)
方法四:
(8+3)×4÷2+(8-3)×10÷2=22+25=47(平方厘米)
典题精讲
易错提醒
数学门诊。(下面的解答对吗?不对的请改正)
一块铁板的形状如图。在这块铁板的一面涂上油漆,涂油漆的面积是多少?(单位:分米)
解答:(2+4+2)÷2=4(分米)
(8+10)×4÷2×2=72(平方分米) ( )
改正:
×
辨析:分割图形错误,分割方法没有根据。
2+4+2=8(分米) 8×8=64(平方分米)
(4+8)×(10-8)÷2=12(平方分米)
64+12=76(平方分米)
03
学以致用
小试牛刀
1. 计算下面组合图形的面积。(单位:cm)
(8+16)×(16-9)÷2=84(cm2)
16×9=144(cm2)
84+144=228(cm2)
25×15=375(cm2)
(20-15)×(25-15)÷2=25(cm2)
375+25=400(cm2)
小试牛刀
2. 一块菜地(如下图),求它的面积。(单位:m)
18×18÷2=162(m2)
(18+12)×22÷2=330(m2)
162+330=492(m2)
3. 一块梯形稻田,中间有一条水渠通过。
(1)实际种植水稻的面积是多少平方米?
(2)如果每平方米稻田产水稻1.2千克,那么这块稻田共产水稻多少千克?
934.5×1.2=1121.4(千克)
(44+48)×21÷2=966(m2) 1.5×21=31.5(m2)
966-31.5=934.5(m2)
04
课堂小结
归纳总结:
求组合图形面积的基本方法:
1.观察分析组合图形可分割或添补成哪些已经学过的基本图形。
2.找出计算基本图形面积需要的条件。
3.利用合理的方法,先计算出基本图形的面积,再计算出组合图形的面积。
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
