人教A版必修五2.4等比数列3 (第一课时)课件(共14张PPT)
文档属性
| 名称 | 人教A版必修五2.4等比数列3 (第一课时)课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览



文档简介
(共14张PPT)
名称 等差数列
概 念
常数
性质
通项
通项 变形
旧知回顾
从第2项起,每一项与它前一项的差等同一个常数
公差(d)
d可正可负,且可以为零
前n项和公式:
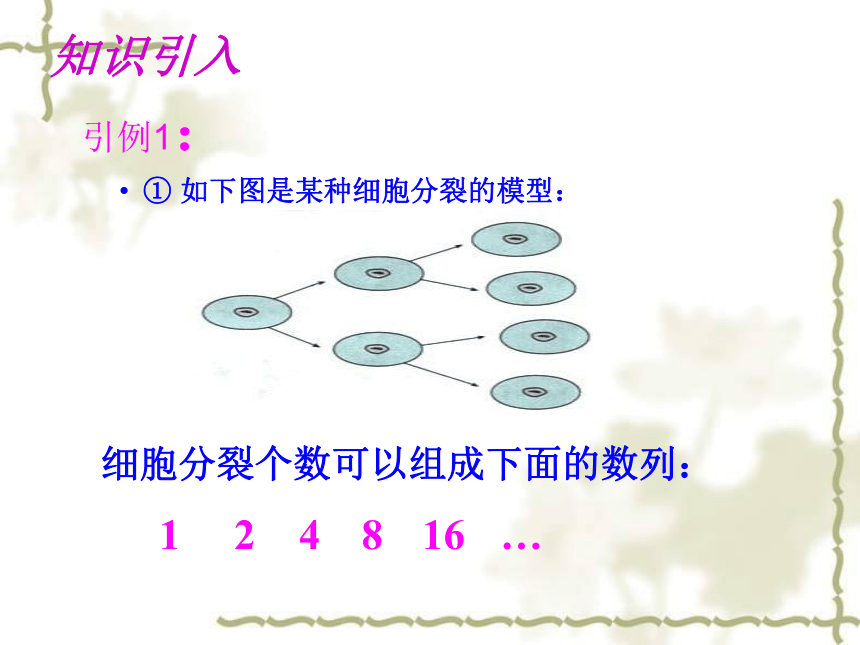
引例1:
① 如下图是某种细胞分裂的模型:
细胞分裂个数可以组成下面的数列:
1
2
4
8
16
…
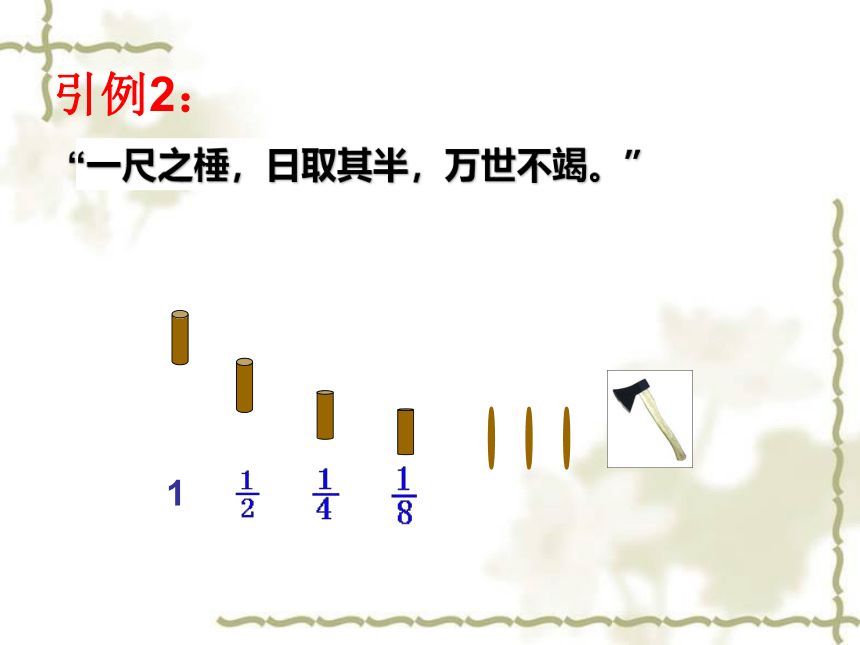
知识引入
1
“一尺之棰,日取其半,万世不竭。”
引例2:
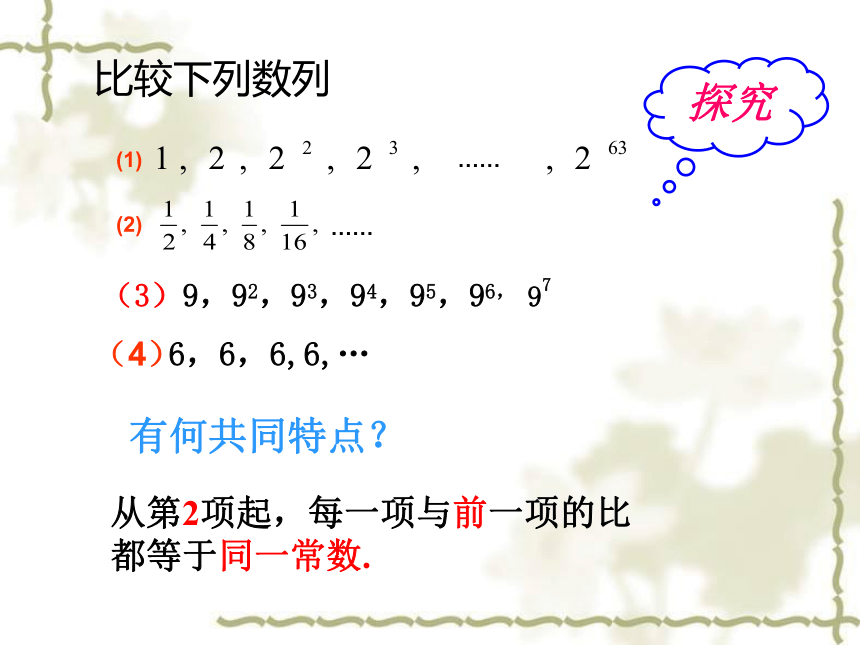
比较下列数列
有何共同特点?
从第2项起,每一项与前一项的比都等于同一常数.
(1)
……
(2)
……
(3)9,92,93,94,95,96, 97
6,6,6,6,…
(4)
探究
1、等比数列的概念
一般的,如果一个数列从第2项起,每一项与它前一项的比等于同一个常数,这个数列就叫做等比数列。这个常数叫做等比数列的公比,公比通常用字母q表示。(q≠0)
符号表示为:
(q为常数)
想一想?
在等比数列中,q可不可以等于1呢?q=1又是什么数列呢?
在等比数列中,q=1是一个非零常数列
(2) 2,-2,2,-2,…
(4) 0,2,0,2,0,2,…
(5) a, a2, a3, a4,……
例1、判断以下数列是等比数列吗?如果是,说出它的公比
(1)5,25,125,625…
(3) 2,-4,8,-16…
是,q=5
是,q=-1
是,q=-2
不是
当a=0时,不是
否则是,q=a
注意:等比数列中
公比q≠0,则an≠0(n∈N);
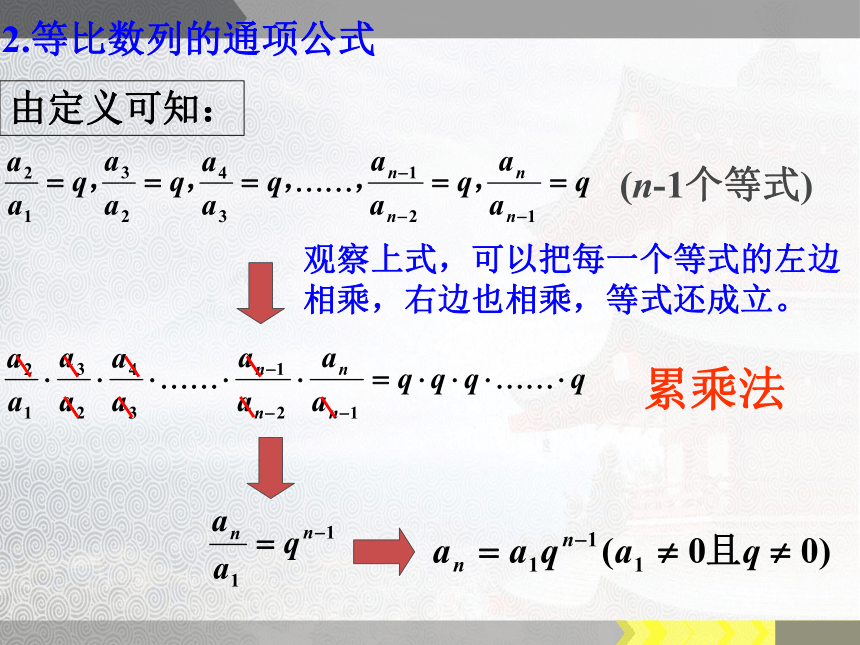
由定义可知:
观察上式,可以把每一个等式的左边相乘,右边也相乘,等式还成立。
累乘法
2.等比数列的通项公式
(n-1个等式)
例2:一个等比数列的第3项与第4项分别是12与18,求它的第1项与第2项.
用 表示题中公比为q的等比数列,由已知条件,有
解得
因此,
答:这个数列的第1项与第2项分别是
解:
(1)a4=27,q=-3, 求an;
练习、在等比数列{an}中
(2)a2=18,a4=8,求a1与q;
(3)a5-a1=15,a4-a2=6,求an
二.等比中项
在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项。
思考一:2,-6之间是否存在等比中项?
思考二:1和4的等比中项是什么?
、
例2 已知等比数列{an}中,
求
课后小结:
一、等比数列的定义:
二、等比数列的通项公式:
三、数学方法及思想:
归纳法、方程思想
数 列 等 差 数 列 等 比 数 列
定 义
公差(比)
通项公式
引申
类比
3、等差数列与等比数列的比较
名称 等差数列
概 念
常数
性质
通项
通项 变形
旧知回顾
从第2项起,每一项与它前一项的差等同一个常数
公差(d)
d可正可负,且可以为零
前n项和公式:
引例1:
① 如下图是某种细胞分裂的模型:
细胞分裂个数可以组成下面的数列:
1
2
4
8
16
…
知识引入
1
“一尺之棰,日取其半,万世不竭。”
引例2:
比较下列数列
有何共同特点?
从第2项起,每一项与前一项的比都等于同一常数.
(1)
……
(2)
……
(3)9,92,93,94,95,96, 97
6,6,6,6,…
(4)
探究
1、等比数列的概念
一般的,如果一个数列从第2项起,每一项与它前一项的比等于同一个常数,这个数列就叫做等比数列。这个常数叫做等比数列的公比,公比通常用字母q表示。(q≠0)
符号表示为:
(q为常数)
想一想?
在等比数列中,q可不可以等于1呢?q=1又是什么数列呢?
在等比数列中,q=1是一个非零常数列
(2) 2,-2,2,-2,…
(4) 0,2,0,2,0,2,…
(5) a, a2, a3, a4,……
例1、判断以下数列是等比数列吗?如果是,说出它的公比
(1)5,25,125,625…
(3) 2,-4,8,-16…
是,q=5
是,q=-1
是,q=-2
不是
当a=0时,不是
否则是,q=a
注意:等比数列中
公比q≠0,则an≠0(n∈N);
由定义可知:
观察上式,可以把每一个等式的左边相乘,右边也相乘,等式还成立。
累乘法
2.等比数列的通项公式
(n-1个等式)
例2:一个等比数列的第3项与第4项分别是12与18,求它的第1项与第2项.
用 表示题中公比为q的等比数列,由已知条件,有
解得
因此,
答:这个数列的第1项与第2项分别是
解:
(1)a4=27,q=-3, 求an;
练习、在等比数列{an}中
(2)a2=18,a4=8,求a1与q;
(3)a5-a1=15,a4-a2=6,求an
二.等比中项
在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项。
思考一:2,-6之间是否存在等比中项?
思考二:1和4的等比中项是什么?
、
例2 已知等比数列{an}中,
求
课后小结:
一、等比数列的定义:
二、等比数列的通项公式:
三、数学方法及思想:
归纳法、方程思想
数 列 等 差 数 列 等 比 数 列
定 义
公差(比)
通项公式
引申
类比
3、等差数列与等比数列的比较
