节节高高中数学北师大版(2019)必修第一册第一章——2.1必要条件与充分条件A(Word版含解析)
文档属性
| 名称 | 节节高高中数学北师大版(2019)必修第一册第一章——2.1必要条件与充分条件A(Word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 348.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览




文档简介
节节高高中数学北师大版(2019)必修第一册第一章——2.1必要条件与充分条件A
未命名
一、单选题
1.设,则""是""的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.已知直线:,:,,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.已知命题:,:为偶函数,则是成立的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
4.“直线与平行”是“直线与的斜率相等”的( )条件
A.充分非必要 B.必要非充分
C.充要 D.既非充分又非必要
5.2022年3月21日,东方航空公司MU5735航班在广西梧州市上空失联并坠毁.专家指出:飞机坠毁原因需要找到飞机自带的两部飞行记录器(黑匣子),如果两部黑匣子都被找到,那么就能形成一个初步的事故原因认定.3月23日16时30分左右,广西武警官兵找到一个黑匣子,虽其外表遭破坏,但内部存储设备完整,研究判定为驾驶员座舱录音器.则“找到驾驶员座舱录音器”是“初步事故原因认定”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
6.已知,,则是的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.非充分非必要条件
二、多选题
7.使得或成立的充分非必要条件有( ).
A. B.
C. D.
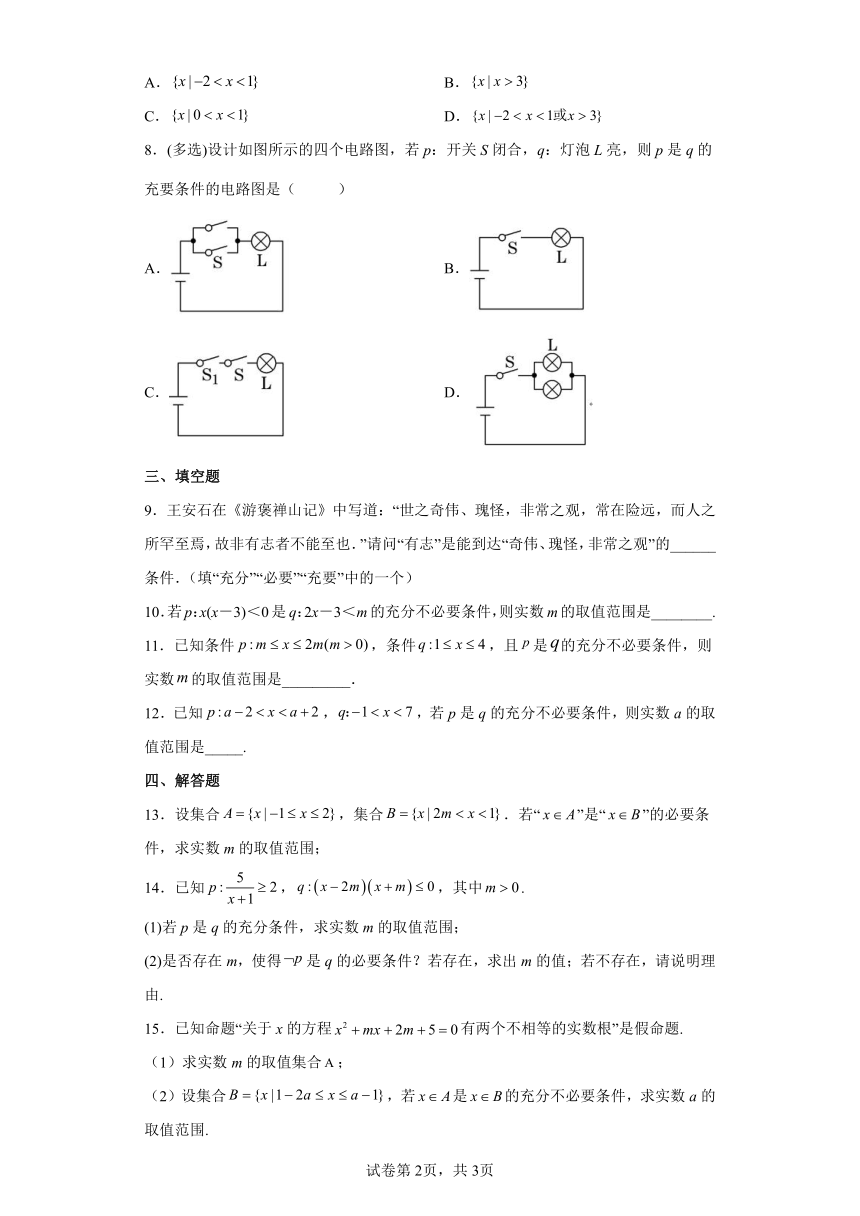
8.(多选)设计如图所示的四个电路图,若p:开关S闭合,q:灯泡L亮,则p是q的充要条件的电路图是( )
A. B.
C. D.
三、填空题
9.王安石在《游褒禅山记》中写道:“世之奇伟、瑰怪,非常之观,常在险远,而人之所罕至焉,故非有志者不能至也.”请问“有志”是能到达“奇伟、瑰怪,非常之观”的______条件.(填“充分”“必要”“充要”中的一个)
10.若p:x(x-3)<0是q:2x-3<m的充分不必要条件,则实数m的取值范围是________.
11.已知条件,条件,且是的充分不必要条件,则实数的取值范围是_________.
12.已知,,若p是q的充分不必要条件,则实数a的取值范围是_____.
四、解答题
13.设集合,集合.若“”是“”的必要条件,求实数m的取值范围;
14.已知,,其中.
(1)若p是q的充分条件,求实数m的取值范围;
(2)是否存在m,使得是q的必要条件?若存在,求出m的值;若不存在,请说明理由.
15.已知命题“关于x的方程有两个不相等的实数根”是假命题.
(1)求实数m的取值集合;
(2)设集合,若是的充分不必要条件,求实数a的取值范围.
16.已知集合,.
(1)用区间表示集合P;
(2)是否存在实数m,使得是的______条件.若存在实数m,求出m的取值范围:若不存在,请说明理由.
请从如下三个条件选择一个条件补充到上面的横线上:
①充分不必要;②必要不充分;③充要.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
用集合法判断即可.
【详解】
因为集合是集合的真子集,
所以“”是“”的必要不充分条件.
故选:B.
【点睛】
结论点睛:有关充要条件类问题的判断,一般可根据如下规则判断:
(1)若是的必要不充分条件,则对应集合是对应集合的真子集;
(2)若是的充分不必要条件, 则对应集合是对应集合的真子集;
(3)若是的充分必要条件,则对应集合与对应集合相等;
(4)若是的既不充分又不必要条件,对应集合与对应集合互不包含.
2.A
【解析】
【分析】
根据直线与直线的垂直,列方程,求出,再判断充分性和必要性即可.
【详解】
解:若,则,解得或,
即或,
所以“”是“或”的充分不必要条件.
故选:A.
【点睛】
本题考查直线一般式中直线与直线垂直的系数关系,考查充分性和必要性的判断,是基础题.
3.C
【解析】
【分析】
求出命题的充要条件,然后确定题中选项.
【详解】
为偶函数,则恒成立,
,,,整理得,所以.
所以是的充分必要条件.
故选:C.
【点睛】
本题考查充分必要条件的判断.掌握充分必要条件的概念是解题关键.
4.D
【解析】
【分析】
根据直线平行与斜率之间的关系,逐个选项进行判断即可.
【详解】
充分性:直线与平行,但是和都没有斜率,即当和都垂直于轴时,与仍然平行,但是,此时不满足直线与的斜率相等,故充分性不成立;
必要性:直线与的斜率相等,则直线与平行或重合,故必要性不成立;
综上,“直线与平行”是“直线与的斜率相等”的既非充分又非必要条件.
故选:D
5.C
【解析】
【分析】
因为两部黑匣子都被找到,就能形成一个初步的事故原因认定,根据充分与必要条件的定义即可判断出结果.
【详解】
因为两部黑匣子都被找到,就能形成一个初步的事故原因认定,
则“找到驾驶员座舱录音器”不能形成“初步事故原因认定”;
而形成“初步事故原因认定”则表示已经“找到驾驶员座舱录音器”,
故“找到驾驶员座舱录音器”是“初步事故原因认定”的必要不充分条件,
故选:C.
6.B
【解析】
【分析】
直接利用不等式的性质判断充分条件和必要条件.
【详解】
解:对于命题,可得到,但是与9没有关系,
当命题,整理,
即得到,故是的必要不充分条件.
故选:B.
【点睛】
本题考查不等式的性质以及利用等价法判断必要不充分条件,考查学生的运算和推理能力,属于基础题.
7.ABC
【解析】
【分析】
求使得或成立的充分非必要条件,则“选项”为的集合是题目条件集合的真子集.
【详解】
求使得或成立的充分非必要条件,
故“选项”为条件p,“或”为结论q,
是的充分非必要条件,设p:“”,q:“”,是的真子集.
故选:ABC.
8.BD
【解析】
【分析】
利用充分条件,必要条件和充要条件的定义判断.
【详解】
电路图A中,开关S闭合,灯泡L亮,而灯泡L亮开关S不一定闭合,故A中p是q的充分不必要条件;
电路图B中,开关S闭合,灯泡L亮,且灯泡L亮,则开关S一定闭合,故B中p是q的充要条件;
电路图C中,开关S闭合,灯泡L不一定亮,灯泡L亮则开关S一定闭合,故C中p是q的必要不充分条件;
电路图D中,开关S闭合则灯泡L亮,灯泡L亮则一定有开关S闭合,故D中p是q的充要条件.
故选:BD.
9.必要
【解析】
【分析】
根据充分条件、必要条件的判定方法,即可求解.
【详解】
因为“非有志者不能至”所以“能至是有志者”,因此“有志”是能到达“奇伟、瑰怪,非常之观”的必要条件.
故答案为:必要
10.m≥3
【解析】
【分析】
先化简命题p,q,再根据p是q的充分不必要条件,由求解.
【详解】
p:x(x-3)<0,则0<x<3;q:2x-3<m,则,
因为p:x(x-3)<0是q:2x-3<m的充分不必要条件,
所以,
解得m≥3.
故答案为:m≥3
11.
【解析】
由题可得 ,可求解.
【详解】
是的充分不必要条件,
,
需满足,解得,
综上,的取值范围是.
故答案为:.
【点睛】
结论点睛:本题考查根据充分不必要条件求参数,一般可根据如下规则判断:
(1)若是的必要不充分条件,则对应集合是对应集合的真子集;
(2)若是的充分不必要条件,则对应集合是对应集合的真子集;
(3)若是的充分必要条件,则对应集合与对应集合相等;
(4)若是的既不充分又不必要条件,则对应的集合与对应集合互不包含.
12.
【解析】
【分析】
根据p是q的充分不必要条件,所以,然后建立关系式,解之即可.
【详解】
解:,,
因为p是q的充分不必要条件,所以,
则,即.
经检验满足条件.
故答案为: .
13..
【解析】
由“”是“”的必要条件有,讨论、满足条件时m的范围,最后求并集即可.
【详解】
若“”是“”的必要条件,则,
,
①当时,,此时,即;
②当时,,有成立;
∴综上所述,所求的取值范围是.
14.(1)
(2)不存在,理由见解析.
【解析】
【分析】
分别求出命题与命题,再根据充分条件与必要条件即可解出答案.
(1)
命题.
命题.
若p是q的充分条件,则
即
(2)
:或.
是q的必要条件,则
即或;解得:或;又
故不存在使是q的必要条件.
【点睛】
本题考查充分必要条件.属于基础题.解本类题型常用“小范围可以推大范围,大范围不能推小范围”来解决.
15.(1);(2).
【解析】
(1)先令求出方程有两个不相等的实数根”是真命题时的范围,再求补集即可;
(2)由题意可知 ,可得,解出,再检验端点值即可.
【详解】
(1)若关于x的方程有两个不相等的实数根”是真命题,
则,即,
解得:或,
所以方程有两个不相等的实数根”是假命题则,
所以,
(2)是的充分不必要条件,则 ,
则,解得,
经检验时,,满足 ,所以成立,
所以实数a的取值范围是.
【点睛】
结论点睛:本题考查充分不必要条件的判断,一般可根据如下规则判断:
(1)若是的必要不充分条件,则对应集合是对应集合的真子集;
(2)是的充分不必要条件, 则对应集合是对应集合的真子集;
(3)是的充分必要条件,则对应集合与对应集合相等;
(4)是的既不充分又不必要条件, 对的集合与对应集合互不包含.
16.(1);(2)答案见解析.
【解析】
(1)解不等式后可得集合.
(2)根据条件关系可得对应集合的包含关系,从而可得参数的取值范围.
【详解】
(1)因为即,所以,
.
(2)若选择①,即是的充分不必要条件,
则且(两个等号不同时成立),
解得,故实数m的取值范围是.
若选择②,即是的必要不充分条件.
当时,,解得.
当时,且(两个等号不同时成立),
解得.
综上,实数m的取值范围是.
若选择③,即是的充要条件,
则,即此方程组无解,
则不存在实数m,使是的充要条件.
【点睛】
方法点睛:
(1)若是的必要不充分条件,则对应集合是对应集合的真子集;
(2)是的充分不必要条件, 则对应集合是对应集合的真子集;
(3)是的充分必要条件,则对应集合与对应集合相等;
(4)是的既不充分又不必要条件, 对的集合与对应集合互不包含.
答案第1页,共2页
答案第1页,共2页
未命名
一、单选题
1.设,则""是""的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.已知直线:,:,,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.已知命题:,:为偶函数,则是成立的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
4.“直线与平行”是“直线与的斜率相等”的( )条件
A.充分非必要 B.必要非充分
C.充要 D.既非充分又非必要
5.2022年3月21日,东方航空公司MU5735航班在广西梧州市上空失联并坠毁.专家指出:飞机坠毁原因需要找到飞机自带的两部飞行记录器(黑匣子),如果两部黑匣子都被找到,那么就能形成一个初步的事故原因认定.3月23日16时30分左右,广西武警官兵找到一个黑匣子,虽其外表遭破坏,但内部存储设备完整,研究判定为驾驶员座舱录音器.则“找到驾驶员座舱录音器”是“初步事故原因认定”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
6.已知,,则是的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.非充分非必要条件
二、多选题
7.使得或成立的充分非必要条件有( ).
A. B.
C. D.
8.(多选)设计如图所示的四个电路图,若p:开关S闭合,q:灯泡L亮,则p是q的充要条件的电路图是( )
A. B.
C. D.
三、填空题
9.王安石在《游褒禅山记》中写道:“世之奇伟、瑰怪,非常之观,常在险远,而人之所罕至焉,故非有志者不能至也.”请问“有志”是能到达“奇伟、瑰怪,非常之观”的______条件.(填“充分”“必要”“充要”中的一个)
10.若p:x(x-3)<0是q:2x-3<m的充分不必要条件,则实数m的取值范围是________.
11.已知条件,条件,且是的充分不必要条件,则实数的取值范围是_________.
12.已知,,若p是q的充分不必要条件,则实数a的取值范围是_____.
四、解答题
13.设集合,集合.若“”是“”的必要条件,求实数m的取值范围;
14.已知,,其中.
(1)若p是q的充分条件,求实数m的取值范围;
(2)是否存在m,使得是q的必要条件?若存在,求出m的值;若不存在,请说明理由.
15.已知命题“关于x的方程有两个不相等的实数根”是假命题.
(1)求实数m的取值集合;
(2)设集合,若是的充分不必要条件,求实数a的取值范围.
16.已知集合,.
(1)用区间表示集合P;
(2)是否存在实数m,使得是的______条件.若存在实数m,求出m的取值范围:若不存在,请说明理由.
请从如下三个条件选择一个条件补充到上面的横线上:
①充分不必要;②必要不充分;③充要.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
用集合法判断即可.
【详解】
因为集合是集合的真子集,
所以“”是“”的必要不充分条件.
故选:B.
【点睛】
结论点睛:有关充要条件类问题的判断,一般可根据如下规则判断:
(1)若是的必要不充分条件,则对应集合是对应集合的真子集;
(2)若是的充分不必要条件, 则对应集合是对应集合的真子集;
(3)若是的充分必要条件,则对应集合与对应集合相等;
(4)若是的既不充分又不必要条件,对应集合与对应集合互不包含.
2.A
【解析】
【分析】
根据直线与直线的垂直,列方程,求出,再判断充分性和必要性即可.
【详解】
解:若,则,解得或,
即或,
所以“”是“或”的充分不必要条件.
故选:A.
【点睛】
本题考查直线一般式中直线与直线垂直的系数关系,考查充分性和必要性的判断,是基础题.
3.C
【解析】
【分析】
求出命题的充要条件,然后确定题中选项.
【详解】
为偶函数,则恒成立,
,,,整理得,所以.
所以是的充分必要条件.
故选:C.
【点睛】
本题考查充分必要条件的判断.掌握充分必要条件的概念是解题关键.
4.D
【解析】
【分析】
根据直线平行与斜率之间的关系,逐个选项进行判断即可.
【详解】
充分性:直线与平行,但是和都没有斜率,即当和都垂直于轴时,与仍然平行,但是,此时不满足直线与的斜率相等,故充分性不成立;
必要性:直线与的斜率相等,则直线与平行或重合,故必要性不成立;
综上,“直线与平行”是“直线与的斜率相等”的既非充分又非必要条件.
故选:D
5.C
【解析】
【分析】
因为两部黑匣子都被找到,就能形成一个初步的事故原因认定,根据充分与必要条件的定义即可判断出结果.
【详解】
因为两部黑匣子都被找到,就能形成一个初步的事故原因认定,
则“找到驾驶员座舱录音器”不能形成“初步事故原因认定”;
而形成“初步事故原因认定”则表示已经“找到驾驶员座舱录音器”,
故“找到驾驶员座舱录音器”是“初步事故原因认定”的必要不充分条件,
故选:C.
6.B
【解析】
【分析】
直接利用不等式的性质判断充分条件和必要条件.
【详解】
解:对于命题,可得到,但是与9没有关系,
当命题,整理,
即得到,故是的必要不充分条件.
故选:B.
【点睛】
本题考查不等式的性质以及利用等价法判断必要不充分条件,考查学生的运算和推理能力,属于基础题.
7.ABC
【解析】
【分析】
求使得或成立的充分非必要条件,则“选项”为的集合是题目条件集合的真子集.
【详解】
求使得或成立的充分非必要条件,
故“选项”为条件p,“或”为结论q,
是的充分非必要条件,设p:“”,q:“”,是的真子集.
故选:ABC.
8.BD
【解析】
【分析】
利用充分条件,必要条件和充要条件的定义判断.
【详解】
电路图A中,开关S闭合,灯泡L亮,而灯泡L亮开关S不一定闭合,故A中p是q的充分不必要条件;
电路图B中,开关S闭合,灯泡L亮,且灯泡L亮,则开关S一定闭合,故B中p是q的充要条件;
电路图C中,开关S闭合,灯泡L不一定亮,灯泡L亮则开关S一定闭合,故C中p是q的必要不充分条件;
电路图D中,开关S闭合则灯泡L亮,灯泡L亮则一定有开关S闭合,故D中p是q的充要条件.
故选:BD.
9.必要
【解析】
【分析】
根据充分条件、必要条件的判定方法,即可求解.
【详解】
因为“非有志者不能至”所以“能至是有志者”,因此“有志”是能到达“奇伟、瑰怪,非常之观”的必要条件.
故答案为:必要
10.m≥3
【解析】
【分析】
先化简命题p,q,再根据p是q的充分不必要条件,由求解.
【详解】
p:x(x-3)<0,则0<x<3;q:2x-3<m,则,
因为p:x(x-3)<0是q:2x-3<m的充分不必要条件,
所以,
解得m≥3.
故答案为:m≥3
11.
【解析】
由题可得 ,可求解.
【详解】
是的充分不必要条件,
,
需满足,解得,
综上,的取值范围是.
故答案为:.
【点睛】
结论点睛:本题考查根据充分不必要条件求参数,一般可根据如下规则判断:
(1)若是的必要不充分条件,则对应集合是对应集合的真子集;
(2)若是的充分不必要条件,则对应集合是对应集合的真子集;
(3)若是的充分必要条件,则对应集合与对应集合相等;
(4)若是的既不充分又不必要条件,则对应的集合与对应集合互不包含.
12.
【解析】
【分析】
根据p是q的充分不必要条件,所以,然后建立关系式,解之即可.
【详解】
解:,,
因为p是q的充分不必要条件,所以,
则,即.
经检验满足条件.
故答案为: .
13..
【解析】
由“”是“”的必要条件有,讨论、满足条件时m的范围,最后求并集即可.
【详解】
若“”是“”的必要条件,则,
,
①当时,,此时,即;
②当时,,有成立;
∴综上所述,所求的取值范围是.
14.(1)
(2)不存在,理由见解析.
【解析】
【分析】
分别求出命题与命题,再根据充分条件与必要条件即可解出答案.
(1)
命题.
命题.
若p是q的充分条件,则
即
(2)
:或.
是q的必要条件,则
即或;解得:或;又
故不存在使是q的必要条件.
【点睛】
本题考查充分必要条件.属于基础题.解本类题型常用“小范围可以推大范围,大范围不能推小范围”来解决.
15.(1);(2).
【解析】
(1)先令求出方程有两个不相等的实数根”是真命题时的范围,再求补集即可;
(2)由题意可知 ,可得,解出,再检验端点值即可.
【详解】
(1)若关于x的方程有两个不相等的实数根”是真命题,
则,即,
解得:或,
所以方程有两个不相等的实数根”是假命题则,
所以,
(2)是的充分不必要条件,则 ,
则,解得,
经检验时,,满足 ,所以成立,
所以实数a的取值范围是.
【点睛】
结论点睛:本题考查充分不必要条件的判断,一般可根据如下规则判断:
(1)若是的必要不充分条件,则对应集合是对应集合的真子集;
(2)是的充分不必要条件, 则对应集合是对应集合的真子集;
(3)是的充分必要条件,则对应集合与对应集合相等;
(4)是的既不充分又不必要条件, 对的集合与对应集合互不包含.
16.(1);(2)答案见解析.
【解析】
(1)解不等式后可得集合.
(2)根据条件关系可得对应集合的包含关系,从而可得参数的取值范围.
【详解】
(1)因为即,所以,
.
(2)若选择①,即是的充分不必要条件,
则且(两个等号不同时成立),
解得,故实数m的取值范围是.
若选择②,即是的必要不充分条件.
当时,,解得.
当时,且(两个等号不同时成立),
解得.
综上,实数m的取值范围是.
若选择③,即是的充要条件,
则,即此方程组无解,
则不存在实数m,使是的充要条件.
【点睛】
方法点睛:
(1)若是的必要不充分条件,则对应集合是对应集合的真子集;
(2)是的充分不必要条件, 则对应集合是对应集合的真子集;
(3)是的充分必要条件,则对应集合与对应集合相等;
(4)是的既不充分又不必要条件, 对的集合与对应集合互不包含.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
