湖南省永州市双牌县2021-2022学年八年级下学期期末数学试题(word版含答案)
文档属性
| 名称 | 湖南省永州市双牌县2021-2022学年八年级下学期期末数学试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 23:03:36 | ||
图片预览

文档简介
双牌县2022年上期期末质量监测
八年级数学(试题卷)
温馨提示:
1.本试卷包括试题卷和答题卡.考生作答时,选择题和非选择题均须作答在答题卡上,在本试题卷上作答无效.考生在答题卡上按答题卡中注意事项的要求答题.
2.考试结束后,将本试题卷和答题卡一并交回.
3.本试卷满分150分,考试时间120分钟.本试卷共三道大题,26个小题.如有缺页,考生须声明.
一、选择题(本大题共10个小题,每小题只有一个正确选项,请将正确选项填涂到答题卡上,每小题4分,共40分)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.在平面直角坐标系中,点(3,-2)关于x轴对称的点的坐标是( )
A.(3,2) B.(-3,-2) C.(-3,2) D.(-2,3)
3.在期末体育考核中,成绩分为优秀、合格、不合格三个档次,初一(1)班有48名学生,达到优秀的有15人,合格的有21人,则这次体育考核中,不合格人数的频率是( )
A.0.125 B.0.215 C.0.25 D.1.25
4.如图,已知点A、D、C、F在同一条直线上,,,那么添加下列一个条件后,仍无法判定≌的是( )
A. B. C. D.
5.如图,在中,CD是斜边AB上的中线,若,则的度数为( )
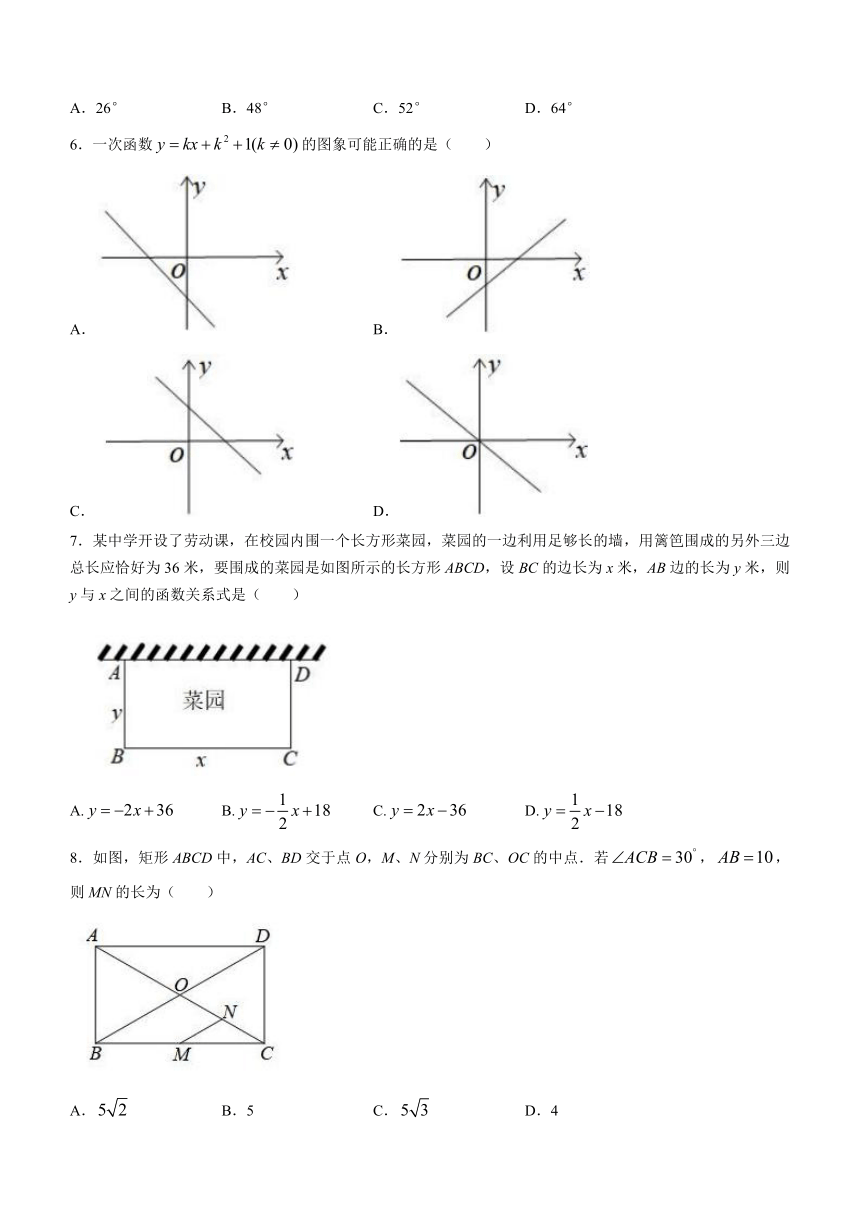
A.26° B.48° C.52° D.64°
6.一次函数的图象可能正确的是( )
A. B.
C. D.
7.某中学开设了劳动课,在校园内围一个长方形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为36米,要围成的菜园是如图所示的长方形ABCD,设BC的边长为x米,AB边的长为y米,则y与x之间的函数关系式是( )
A. B. C. D.
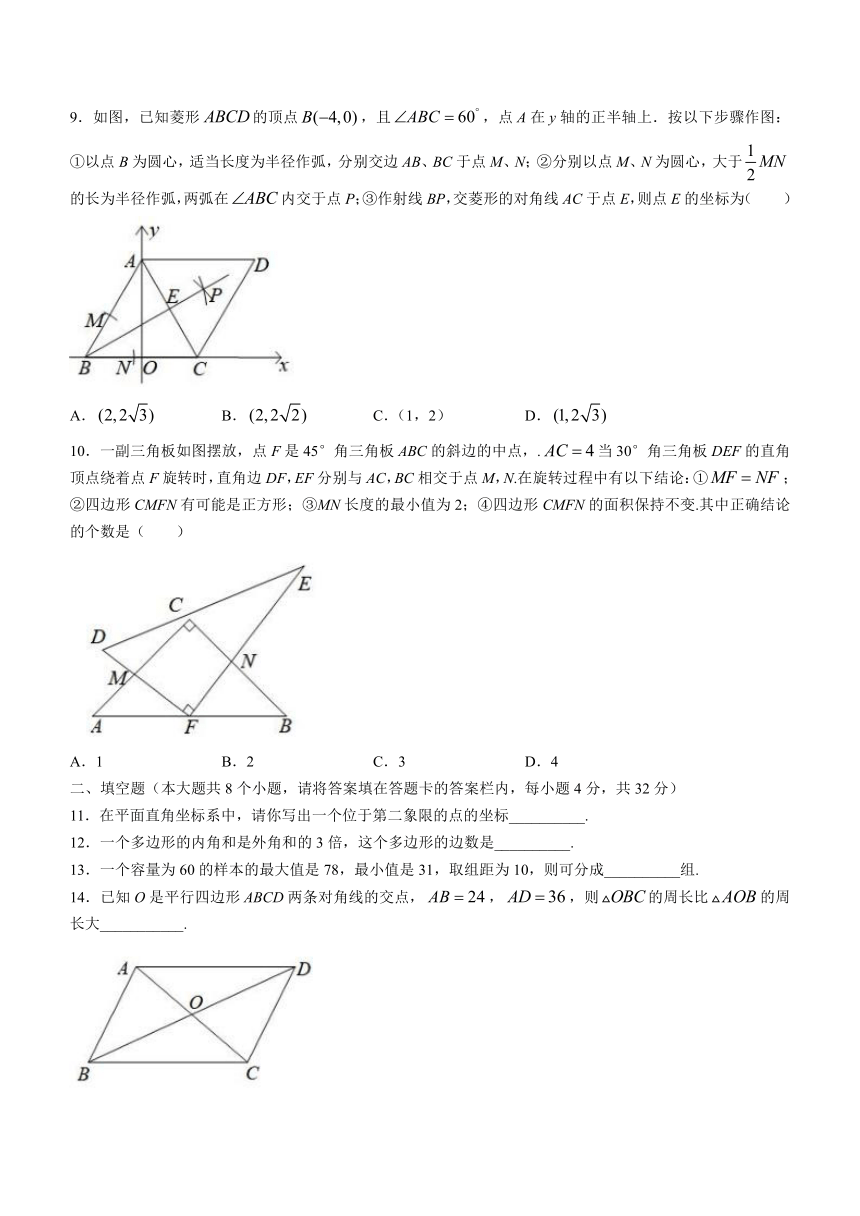
8.如图,矩形ABCD中,AC、BD交于点O,M、N分别为BC、OC的中点.若,,则MN的长为( )
A. B.5 C. D.4
9.如图,已知菱形的顶点,且,点A在y轴的正半轴上.按以下步骤作图:①以点B为圆心,适当长度为半径作弧,分别交边AB、BC于点M、N;②分别以点M、N为圆心,大于的长为半径作弧,两弧在内交于点P;③作射线BP,交菱形的对角线AC于点E,则点E的坐标为( )
A. B. C.(1,2) D.
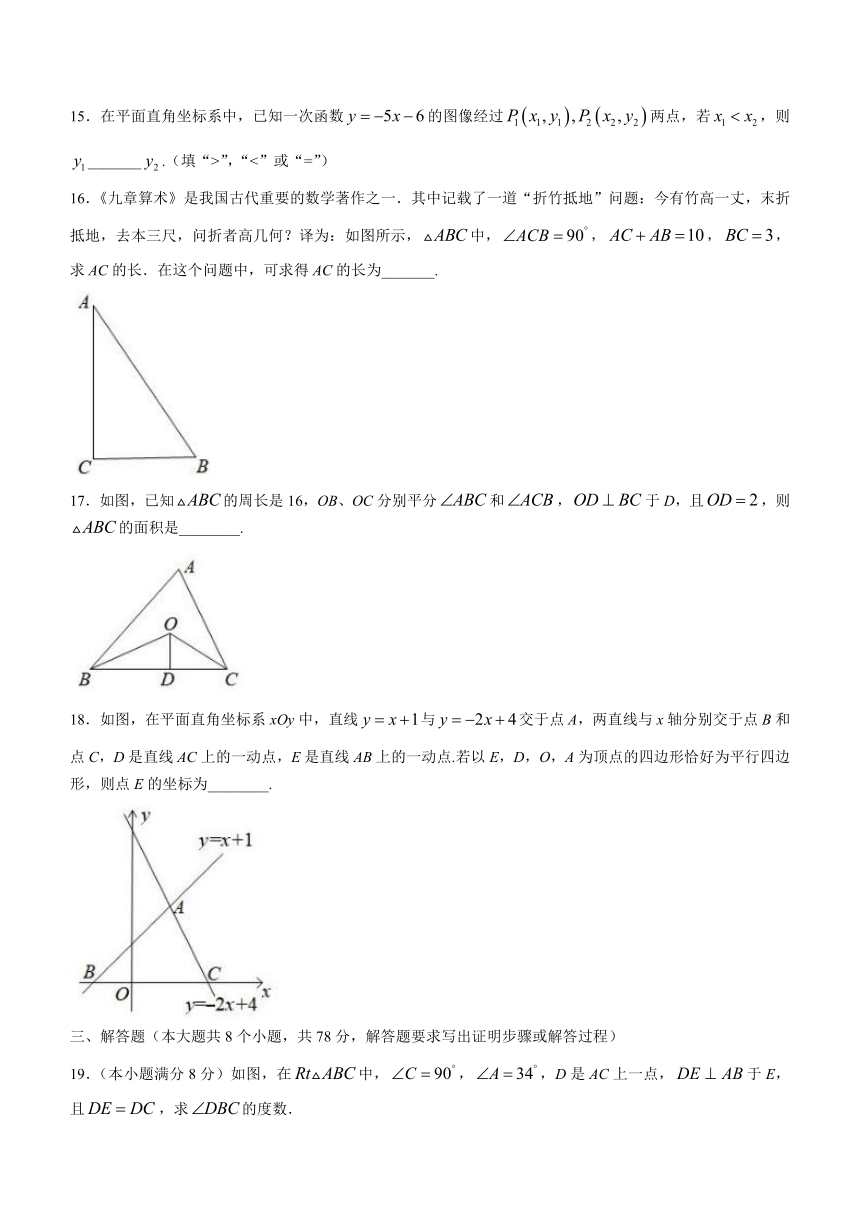
10.一副三角板如图摆放,点F是45°角三角板ABC的斜边的中点,.当30°角三角板DEF的直角顶点绕着点F旋转时,直角边DF,EF分别与AC,BC相交于点M,N.在旋转过程中有以下结论:①;②四边形CMFN有可能是正方形;③MN长度的最小值为2;④四边形CMFN的面积保持不变.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题共8个小题,请将答案填在答题卡的答案栏内,每小题4分,共32分)
11.在平面直角坐标系中,请你写出一个位于第二象限的点的坐标__________.
12.一个多边形的内角和是外角和的3倍,这个多边形的边数是__________.
13.一个容量为60的样本的最大值是78,最小值是31,取组距为10,则可分成__________组.
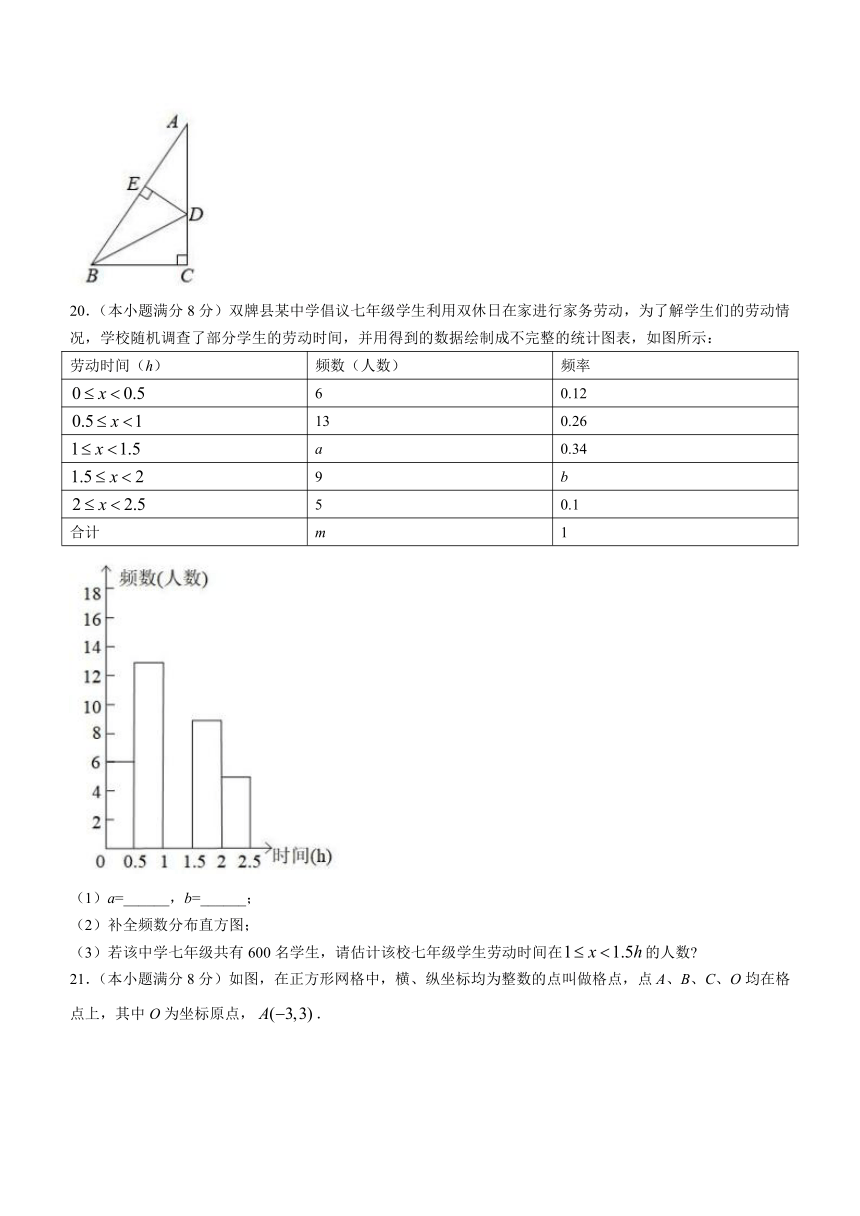
14.已知O是平行四边形ABCD两条对角线的交点,,,则的周长比的周长大___________.
15.在平面直角坐标系中,已知一次函数的图像经过两点,若,则_______.(填“>”,“<”或“=”)
16.《九章算术》是我国古代重要的数学著作之一.其中记载了一道“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?译为:如图所示,中,,,,求AC的长.在这个问题中,可求得AC的长为_______.
17.如图,已知的周长是16,OB、OC分别平分和,于D,且,则的面积是________.
18.如图,在平面直角坐标系xOy中,直线与交于点A,两直线与x轴分别交于点B和点C,D是直线AC上的一动点,E是直线AB上的一动点.若以E,D,O,A为顶点的四边形恰好为平行四边形,则点E的坐标为________.
三、解答题(本大题共8个小题,共78分,解答题要求写出证明步骤或解答过程)
19.(本小题满分8分)如图,在中,,,D是AC上一点,于E,且,求的度数.
20.(本小题满分8分)双牌县某中学倡议七年级学生利用双休日在家进行家务劳动,为了解学生们的劳动情况,学校随机调查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
劳动时间(h) 频数(人数) 频率
6 0.12
13 0.26
a 0.34
9 b
5 0.1
合计 m 1
(1)a=______,b=______;
(2)补全频数分布直方图;
(3)若该中学七年级共有600名学生,请估计该校七年级学生劳动时间在的人数
21.(本小题满分8分)如图,在正方形网格中,横、纵坐标均为整数的点叫做格点,点A、B、C、O均在格点上,其中O为坐标原点,.
(1)点C的坐标为________;
(2)在方格纸内将经过一次平移后得到,图中标出了点A的对应点,请在图中画出平移后的;
(3)求的面积.
22.(本小题满分10分)某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费y(元)与每月用水量x()之间的关系如图所示.
(1)分别求出当和时,y关于x的函数解析式;
(2)若某用户三月份缴纳水费68元,则该用户三月份的用水量是多少?
23.(本小题满分10分)如图,在中,,CD是斜边上的中线,,.
(1)求证:四边形BDCE是菱形;
(2)过点E作,垂足为点F,若点F是BD的中点,,求BC的长.
24.(本小题满分10分)如图,直线和直线相交于点P,分别与y轴交于A,B两点.
(1)求的面积;
(2)在x轴上有一点(其中),过M点作x轴的垂线,与直线交于点C,与直线交于点D,当时,求M点的坐标.
25.(本小题满分12分)如图,在中,点D是边BC的中点,点E在内,AE平分,交AB于G,点F在边AB上,.
(1)若四边形EFBD的面积为6,则的面积是_________;
(2)求证:四边形BDEF是平行四边形;
(3)若,判断BF,AB,CE之间具有怎样的数量关系.
26.(本小题满分12分)我们规定:在平面直角坐标系xOy中,经过象限内某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“参照线”.例如点M(2,1)的参照线有:,,,(如图1).
(1)直接写出点(1,3)的所有参照线;
(2)如图2,正方形OABC在平面直角坐标xOy中,点B的坐标为(8,8),点A,C分别在x轴,y轴上,点在正方形内部.
①点D在线段BA的垂直平分线,且点D有一条“参照线”是,求D点的坐标;
②在①的条件下,点P是AB边上任意一点(不与A,B重合),连接OP,将沿着OP折叠,点A的对应点记为E,当点E落在点D的平行于坐标轴的参照线上时,求出相应的点P的坐标.
双牌县2022年八年级期末考试试卷
数学参考答案及评分标准
一、选择题(本大题共10个小题,每小题只有一个正确选项,请将正确选项填涂到答题卡上,每小题4分,共40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C D C C B B A C
二、填空题(本大题共8个小题,请将答案填在答题卡的答案栏内,每小题4分,共32分)
11.答案不唯一 12.8 13.5 14.12
15.> 16.4.55 17.16 18.或
三、解答题(本大题共8个小题,共78分,解答题要求写出证明步骤或解答过程)
19.(本小题满分8分)
证明:∵,
∴
∵,,
∴BD平分
∴
20.(本小题满分8分)
解:(1),
(2)
(3)
该校七年级学生劳动时间在的人数约为204人
21.(本小题满分8分)
解:(1)(1,4)
(2)
(3)
22.(本小题满分10分)
解:(1)由题意可知,当时,设函数解析式为且过点(15,36)
∴,解得:
∴函数表达式为
当时,设函数解析式为且过点(15,36),(20,52)
∴,解得:
∴函数表达式为
(2)∵
∴
∴
∴则该用户三月份的用水量是
23.(本小题满分10分)
(1)证明:∵,CD是斜边上的中线
∴
∵
∴
∵
∴四边形BDCE是平行四边形
∵
∴四边形BDCE是菱形
(2)四边形BDCE是菱形,
∴
∵点F是BD的中点,
∴,
∴,
∴,
∴
∴
∴
24.(本小题满分10分)
解:(1)∵直线和直线相交于点P,
∴解得
∴点P的坐标为(2,1)
对于,令,则,故点,
对于,令,则,故点,
则
∴
(2),则点,
D,其中
∴点M位于点P右侧,
,解得4m.
∴
25.(本小题满分12分)
解:(1)3
(2)证明:延长CE交AB于点G
∵
∴
∵AE平分
∴
∵
∵
∴
∵点D是边BC的中点
∴
∴DE是的中位线
∴
∵
∴四边形BDEF是平行四边形
(3)
∵四边形BDEF是平行四边形
∴
∵D,E分别是BC,GC的中点,
∴
∵
∴
∵
∴是等边三角形
∴
∴.
26.(本小题满分12分)
证明:(1),,,
(2)①∵点B的坐标为(8,8),点A,C分别在x轴,y轴上,
点D在线段BA的垂直平分线
∴点D的纵坐标为4
又∵点D有一条“参照线”是,
∴
∴点D坐标为(6,4).
②如图1中,当点E在参照线HM上时,设
∴易知,
∴
∴
在中
∴
∴
∴
如图2中,当点E在参照线DH上时,设
∴易知,,
∴
在中
∴
∴
∴
综上所述,P的坐标为或
八年级数学(试题卷)
温馨提示:
1.本试卷包括试题卷和答题卡.考生作答时,选择题和非选择题均须作答在答题卡上,在本试题卷上作答无效.考生在答题卡上按答题卡中注意事项的要求答题.
2.考试结束后,将本试题卷和答题卡一并交回.
3.本试卷满分150分,考试时间120分钟.本试卷共三道大题,26个小题.如有缺页,考生须声明.
一、选择题(本大题共10个小题,每小题只有一个正确选项,请将正确选项填涂到答题卡上,每小题4分,共40分)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.在平面直角坐标系中,点(3,-2)关于x轴对称的点的坐标是( )
A.(3,2) B.(-3,-2) C.(-3,2) D.(-2,3)
3.在期末体育考核中,成绩分为优秀、合格、不合格三个档次,初一(1)班有48名学生,达到优秀的有15人,合格的有21人,则这次体育考核中,不合格人数的频率是( )
A.0.125 B.0.215 C.0.25 D.1.25
4.如图,已知点A、D、C、F在同一条直线上,,,那么添加下列一个条件后,仍无法判定≌的是( )
A. B. C. D.
5.如图,在中,CD是斜边AB上的中线,若,则的度数为( )
A.26° B.48° C.52° D.64°
6.一次函数的图象可能正确的是( )
A. B.
C. D.
7.某中学开设了劳动课,在校园内围一个长方形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为36米,要围成的菜园是如图所示的长方形ABCD,设BC的边长为x米,AB边的长为y米,则y与x之间的函数关系式是( )
A. B. C. D.
8.如图,矩形ABCD中,AC、BD交于点O,M、N分别为BC、OC的中点.若,,则MN的长为( )
A. B.5 C. D.4
9.如图,已知菱形的顶点,且,点A在y轴的正半轴上.按以下步骤作图:①以点B为圆心,适当长度为半径作弧,分别交边AB、BC于点M、N;②分别以点M、N为圆心,大于的长为半径作弧,两弧在内交于点P;③作射线BP,交菱形的对角线AC于点E,则点E的坐标为( )
A. B. C.(1,2) D.
10.一副三角板如图摆放,点F是45°角三角板ABC的斜边的中点,.当30°角三角板DEF的直角顶点绕着点F旋转时,直角边DF,EF分别与AC,BC相交于点M,N.在旋转过程中有以下结论:①;②四边形CMFN有可能是正方形;③MN长度的最小值为2;④四边形CMFN的面积保持不变.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题共8个小题,请将答案填在答题卡的答案栏内,每小题4分,共32分)
11.在平面直角坐标系中,请你写出一个位于第二象限的点的坐标__________.
12.一个多边形的内角和是外角和的3倍,这个多边形的边数是__________.
13.一个容量为60的样本的最大值是78,最小值是31,取组距为10,则可分成__________组.
14.已知O是平行四边形ABCD两条对角线的交点,,,则的周长比的周长大___________.
15.在平面直角坐标系中,已知一次函数的图像经过两点,若,则_______.(填“>”,“<”或“=”)
16.《九章算术》是我国古代重要的数学著作之一.其中记载了一道“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?译为:如图所示,中,,,,求AC的长.在这个问题中,可求得AC的长为_______.
17.如图,已知的周长是16,OB、OC分别平分和,于D,且,则的面积是________.
18.如图,在平面直角坐标系xOy中,直线与交于点A,两直线与x轴分别交于点B和点C,D是直线AC上的一动点,E是直线AB上的一动点.若以E,D,O,A为顶点的四边形恰好为平行四边形,则点E的坐标为________.
三、解答题(本大题共8个小题,共78分,解答题要求写出证明步骤或解答过程)
19.(本小题满分8分)如图,在中,,,D是AC上一点,于E,且,求的度数.
20.(本小题满分8分)双牌县某中学倡议七年级学生利用双休日在家进行家务劳动,为了解学生们的劳动情况,学校随机调查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
劳动时间(h) 频数(人数) 频率
6 0.12
13 0.26
a 0.34
9 b
5 0.1
合计 m 1
(1)a=______,b=______;
(2)补全频数分布直方图;
(3)若该中学七年级共有600名学生,请估计该校七年级学生劳动时间在的人数
21.(本小题满分8分)如图,在正方形网格中,横、纵坐标均为整数的点叫做格点,点A、B、C、O均在格点上,其中O为坐标原点,.
(1)点C的坐标为________;
(2)在方格纸内将经过一次平移后得到,图中标出了点A的对应点,请在图中画出平移后的;
(3)求的面积.
22.(本小题满分10分)某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费y(元)与每月用水量x()之间的关系如图所示.
(1)分别求出当和时,y关于x的函数解析式;
(2)若某用户三月份缴纳水费68元,则该用户三月份的用水量是多少?
23.(本小题满分10分)如图,在中,,CD是斜边上的中线,,.
(1)求证:四边形BDCE是菱形;
(2)过点E作,垂足为点F,若点F是BD的中点,,求BC的长.
24.(本小题满分10分)如图,直线和直线相交于点P,分别与y轴交于A,B两点.
(1)求的面积;
(2)在x轴上有一点(其中),过M点作x轴的垂线,与直线交于点C,与直线交于点D,当时,求M点的坐标.
25.(本小题满分12分)如图,在中,点D是边BC的中点,点E在内,AE平分,交AB于G,点F在边AB上,.
(1)若四边形EFBD的面积为6,则的面积是_________;
(2)求证:四边形BDEF是平行四边形;
(3)若,判断BF,AB,CE之间具有怎样的数量关系.
26.(本小题满分12分)我们规定:在平面直角坐标系xOy中,经过象限内某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“参照线”.例如点M(2,1)的参照线有:,,,(如图1).
(1)直接写出点(1,3)的所有参照线;
(2)如图2,正方形OABC在平面直角坐标xOy中,点B的坐标为(8,8),点A,C分别在x轴,y轴上,点在正方形内部.
①点D在线段BA的垂直平分线,且点D有一条“参照线”是,求D点的坐标;
②在①的条件下,点P是AB边上任意一点(不与A,B重合),连接OP,将沿着OP折叠,点A的对应点记为E,当点E落在点D的平行于坐标轴的参照线上时,求出相应的点P的坐标.
双牌县2022年八年级期末考试试卷
数学参考答案及评分标准
一、选择题(本大题共10个小题,每小题只有一个正确选项,请将正确选项填涂到答题卡上,每小题4分,共40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C D C C B B A C
二、填空题(本大题共8个小题,请将答案填在答题卡的答案栏内,每小题4分,共32分)
11.答案不唯一 12.8 13.5 14.12
15.> 16.4.55 17.16 18.或
三、解答题(本大题共8个小题,共78分,解答题要求写出证明步骤或解答过程)
19.(本小题满分8分)
证明:∵,
∴
∵,,
∴BD平分
∴
20.(本小题满分8分)
解:(1),
(2)
(3)
该校七年级学生劳动时间在的人数约为204人
21.(本小题满分8分)
解:(1)(1,4)
(2)
(3)
22.(本小题满分10分)
解:(1)由题意可知,当时,设函数解析式为且过点(15,36)
∴,解得:
∴函数表达式为
当时,设函数解析式为且过点(15,36),(20,52)
∴,解得:
∴函数表达式为
(2)∵
∴
∴
∴则该用户三月份的用水量是
23.(本小题满分10分)
(1)证明:∵,CD是斜边上的中线
∴
∵
∴
∵
∴四边形BDCE是平行四边形
∵
∴四边形BDCE是菱形
(2)四边形BDCE是菱形,
∴
∵点F是BD的中点,
∴,
∴,
∴,
∴
∴
∴
24.(本小题满分10分)
解:(1)∵直线和直线相交于点P,
∴解得
∴点P的坐标为(2,1)
对于,令,则,故点,
对于,令,则,故点,
则
∴
(2),则点,
D,其中
∴点M位于点P右侧,
,解得4m.
∴
25.(本小题满分12分)
解:(1)3
(2)证明:延长CE交AB于点G
∵
∴
∵AE平分
∴
∵
∵
∴
∵点D是边BC的中点
∴
∴DE是的中位线
∴
∵
∴四边形BDEF是平行四边形
(3)
∵四边形BDEF是平行四边形
∴
∵D,E分别是BC,GC的中点,
∴
∵
∴
∵
∴是等边三角形
∴
∴.
26.(本小题满分12分)
证明:(1),,,
(2)①∵点B的坐标为(8,8),点A,C分别在x轴,y轴上,
点D在线段BA的垂直平分线
∴点D的纵坐标为4
又∵点D有一条“参照线”是,
∴
∴点D坐标为(6,4).
②如图1中,当点E在参照线HM上时,设
∴易知,
∴
∴
在中
∴
∴
∴
如图2中,当点E在参照线DH上时,设
∴易知,,
∴
在中
∴
∴
∴
综上所述,P的坐标为或
同课章节目录
