11.1.2 三角形的高、中线与角平分线学案
文档属性
| 名称 | 11.1.2 三角形的高、中线与角平分线学案 |  | |
| 格式 | zip | ||
| 文件大小 | 26.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-07 13:07:31 | ||
图片预览

文档简介
课题:三角形的高、中线与角平分线 课型:预习+展示 主备人: 审核人: 班级: 姓名:
【学习目标】 1、掌握三角形的高、中线与角平分线.毛2、会用工具准确画出三角形的高、中线与角平分线, 通过画图了解三角形的三条高(及所在直线)交于一点,三角形的三条中线,三条角平分线等都交于一点.重点:(1)掌握三角形的高、中线与角平分线的概念, 会用工具准确画出三角形的高、中线与角平分线. (2)理解三角形的三条高、三条中线与三条角平分线分别交于一点.难点:(1)三角形平分线与角平分线的区别,三角形的高与垂线的区别.(2)钝角三角形高的画法.
学习过程 学法指导
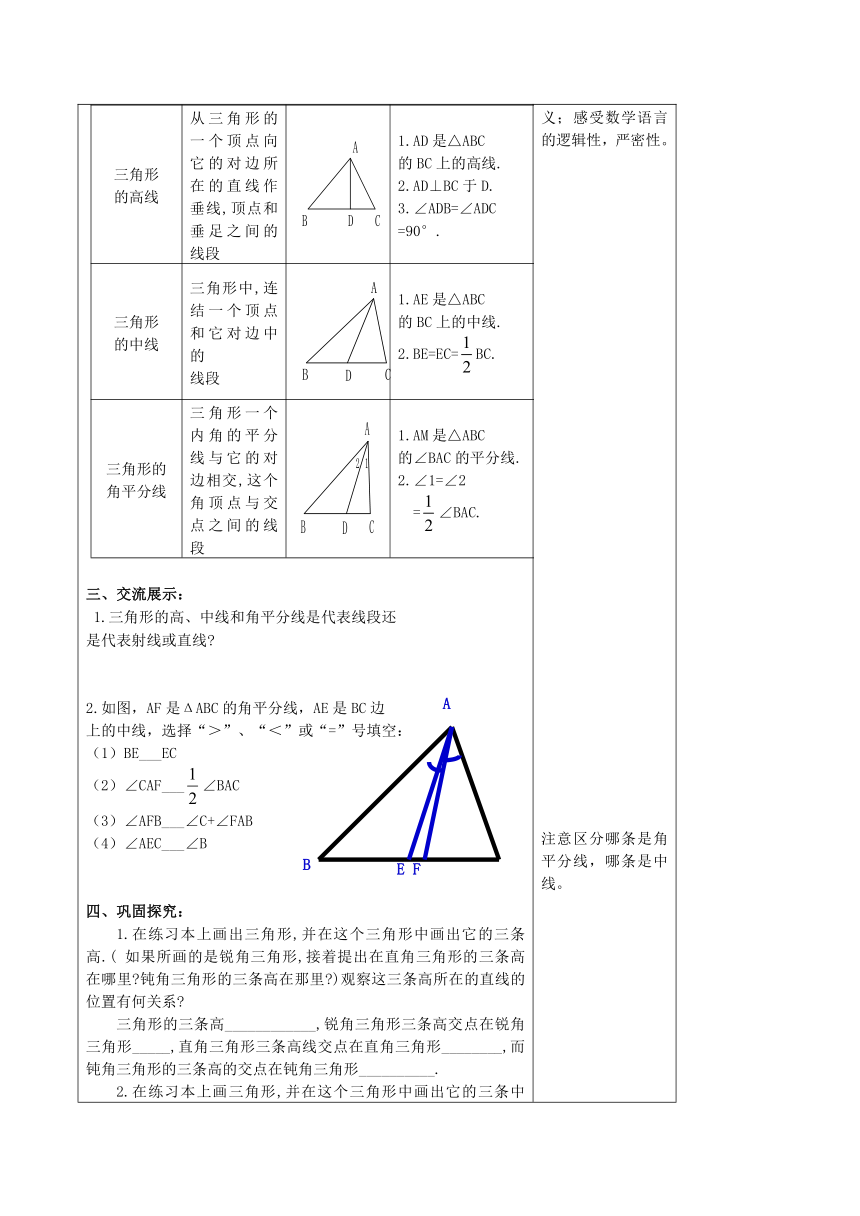
一、复习巩固:1、如果三角形的两边长为2和9,且周长为奇数,那么满足条件的三角形共有( )个。 2、以下列长度的三条线段为边,能构成三角形的是( )A.3,3,3 B.3,3,6 C.3,2,5 D.3,2,63、等腰三角形的两边长分别为12cm和8cm,这个等腰三角形的周长是 。二、自主学习:1.自学内容:课本4页 ----5页2.自学要求:阅读课本内容,仔细观察表中的内容,并回答下面问题.(1)什么叫三角形的高 三角形的高与垂线有何区别和联系 (2)什么叫三角形的中线 连结两点的线段与过两点的直线有何区别和联系 (3)什么叫三角形的角平分线 三角形的角平分线与角平分线有何区别和联系 三角形的重要线段意义图形表示法三角形的高线从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段1.AD是△ABC的BC上的高线.2.AD⊥BC于D.3.∠ADB=∠ADC=90°.三角形的中线三角形中,连结一个顶点和它对边中的线段1.AE是△ABC的BC上的中线.2.BE=EC=BC.三角形的角平分线三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段1.AM是△ABC的∠BAC的平分线.2.∠1=∠2=∠BAC.三、交流展示: 1.三角形的高、中线和角平分线是代表线段还是代表射线或直线 2.如图,AF是ΔABC的角平分线,AE是BC边 上的中线,选择“>”、“<”或“=”号填空:(1)BE___EC(2)∠CAF___∠BAC(3)∠AFB___∠C+∠FAB(4)∠AEC___∠B四、巩固探究: 1.在练习本上画出三角形,并在这个三角形中画出它的三条高.( 如果所画的是锐角三角形,接着提出在直角三角形的三条高在哪里 钝角三角形的三条高在那里 )观察这三条高所在的直线的位置有何关系 三角形的三条高____________,锐角三角形三条高交点在锐角三角形_____,直角三角形三条高线交点在直角三角形________,而钝角三角形的三条高的交点在钝角三角形__________. 2.在练习本上画三角形,并在这个三角形中画出它的三条中线.( 如果所画的是锐角三角形,接着让他们画出直角三角形和钝角三角形,看看这些三角形的中线在哪里) 观察这三条中线的位置有何关系 三角形的三条中线都在三角形________,它们__________,这个交点在______________. 3.在练习本上画一个三角形,并在这三角形中画出它的三条角平分线,观察这三条角平分线的位置有何关系 无论是锐角三角形还是直角三角形或钝角三角形, 它们的三条角平分线都在_________________,并且________.4.课本5页 练习1.2题五、探究拓展 如图,在△ABC中,AE,AD分别是BC边上中线和高,(1)说明△ABE的面积与△AEC的面积有何关系?(2)你有什么发现?同高等底的两个三角形的面积________.三角形的中线把三角形分成两个面积_______的三角形。六、课堂检测1、下列说法错误的是( ).A.三角形的三条高一定在三角形内部交于一点B.三角形的三条中线一定在三角形内部交于一点C.三角形的三条角平分线一定在三角形内部交于一点D.三角形的三条高可能相交于外部一点3、如图,D,E分别是△ABC的边AC,BC的中点,则下列说法错误的是( )A.DE是△BCD的中线 B. BD是△ABC的中线C.AD=DC,BE=EC D. ∠C的对边是DE4、如图,(1)在△ABC中,BC边上的高是 ______;(2)在△AEC中,AE边上的高是 ______;(3)在△FEC中,EC边上的高是 ______;(4)若AB=CD=2cm,AE=3cm,则= ______㎝2,CE=_____cm.5、在△ABC中,D是BC上的点,且BD∶DC=2∶1,=12,那么等于( ).A.30 B. 36 C. 72 D. 246、在△ABC中,AB=AC,AD是中线,△ABC的周长为34cm,△ABD的周长为30cm,求AD的长。 学习要求:注意理解三角形的高、中线与角平分线的意义而不是背其定义;感受数学语言的逻辑性,严密性。注意区分哪条是角平分线,哪条是中线。 相信自己,你是最棒的!
E F
B
A
A
B
D
E
C
注意理解构成三角形的条件
【学习目标】 1、掌握三角形的高、中线与角平分线.毛2、会用工具准确画出三角形的高、中线与角平分线, 通过画图了解三角形的三条高(及所在直线)交于一点,三角形的三条中线,三条角平分线等都交于一点.重点:(1)掌握三角形的高、中线与角平分线的概念, 会用工具准确画出三角形的高、中线与角平分线. (2)理解三角形的三条高、三条中线与三条角平分线分别交于一点.难点:(1)三角形平分线与角平分线的区别,三角形的高与垂线的区别.(2)钝角三角形高的画法.
学习过程 学法指导
一、复习巩固:1、如果三角形的两边长为2和9,且周长为奇数,那么满足条件的三角形共有( )个。 2、以下列长度的三条线段为边,能构成三角形的是( )A.3,3,3 B.3,3,6 C.3,2,5 D.3,2,63、等腰三角形的两边长分别为12cm和8cm,这个等腰三角形的周长是 。二、自主学习:1.自学内容:课本4页 ----5页2.自学要求:阅读课本内容,仔细观察表中的内容,并回答下面问题.(1)什么叫三角形的高 三角形的高与垂线有何区别和联系 (2)什么叫三角形的中线 连结两点的线段与过两点的直线有何区别和联系 (3)什么叫三角形的角平分线 三角形的角平分线与角平分线有何区别和联系 三角形的重要线段意义图形表示法三角形的高线从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段1.AD是△ABC的BC上的高线.2.AD⊥BC于D.3.∠ADB=∠ADC=90°.三角形的中线三角形中,连结一个顶点和它对边中的线段1.AE是△ABC的BC上的中线.2.BE=EC=BC.三角形的角平分线三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段1.AM是△ABC的∠BAC的平分线.2.∠1=∠2=∠BAC.三、交流展示: 1.三角形的高、中线和角平分线是代表线段还是代表射线或直线 2.如图,AF是ΔABC的角平分线,AE是BC边 上的中线,选择“>”、“<”或“=”号填空:(1)BE___EC(2)∠CAF___∠BAC(3)∠AFB___∠C+∠FAB(4)∠AEC___∠B四、巩固探究: 1.在练习本上画出三角形,并在这个三角形中画出它的三条高.( 如果所画的是锐角三角形,接着提出在直角三角形的三条高在哪里 钝角三角形的三条高在那里 )观察这三条高所在的直线的位置有何关系 三角形的三条高____________,锐角三角形三条高交点在锐角三角形_____,直角三角形三条高线交点在直角三角形________,而钝角三角形的三条高的交点在钝角三角形__________. 2.在练习本上画三角形,并在这个三角形中画出它的三条中线.( 如果所画的是锐角三角形,接着让他们画出直角三角形和钝角三角形,看看这些三角形的中线在哪里) 观察这三条中线的位置有何关系 三角形的三条中线都在三角形________,它们__________,这个交点在______________. 3.在练习本上画一个三角形,并在这三角形中画出它的三条角平分线,观察这三条角平分线的位置有何关系 无论是锐角三角形还是直角三角形或钝角三角形, 它们的三条角平分线都在_________________,并且________.4.课本5页 练习1.2题五、探究拓展 如图,在△ABC中,AE,AD分别是BC边上中线和高,(1)说明△ABE的面积与△AEC的面积有何关系?(2)你有什么发现?同高等底的两个三角形的面积________.三角形的中线把三角形分成两个面积_______的三角形。六、课堂检测1、下列说法错误的是( ).A.三角形的三条高一定在三角形内部交于一点B.三角形的三条中线一定在三角形内部交于一点C.三角形的三条角平分线一定在三角形内部交于一点D.三角形的三条高可能相交于外部一点3、如图,D,E分别是△ABC的边AC,BC的中点,则下列说法错误的是( )A.DE是△BCD的中线 B. BD是△ABC的中线C.AD=DC,BE=EC D. ∠C的对边是DE4、如图,(1)在△ABC中,BC边上的高是 ______;(2)在△AEC中,AE边上的高是 ______;(3)在△FEC中,EC边上的高是 ______;(4)若AB=CD=2cm,AE=3cm,则= ______㎝2,CE=_____cm.5、在△ABC中,D是BC上的点,且BD∶DC=2∶1,=12,那么等于( ).A.30 B. 36 C. 72 D. 246、在△ABC中,AB=AC,AD是中线,△ABC的周长为34cm,△ABD的周长为30cm,求AD的长。 学习要求:注意理解三角形的高、中线与角平分线的意义而不是背其定义;感受数学语言的逻辑性,严密性。注意区分哪条是角平分线,哪条是中线。 相信自己,你是最棒的!
E F
B
A
A
B
D
E
C
注意理解构成三角形的条件
