11.2.2 三角形的外角学案
文档属性
| 名称 | 11.2.2 三角形的外角学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 34.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-07 13:09:48 | ||
图片预览

文档简介
课题:三角形的外角 课型:预习+展示 主备人: 审核人: 班级: 姓名:
【学习目标】 1、知识与技能: 掌握三角形内角和定理的两个推论,并会应用.。2、过程与方法:总结知识内容,使之条理化,加深理解和记忆,养成良好的学习习惯。重点:三角形内角和定理推论的应用.难点:三角形外角的概念.真正理解推论,并能灵活运用.
学习过程 学法指导
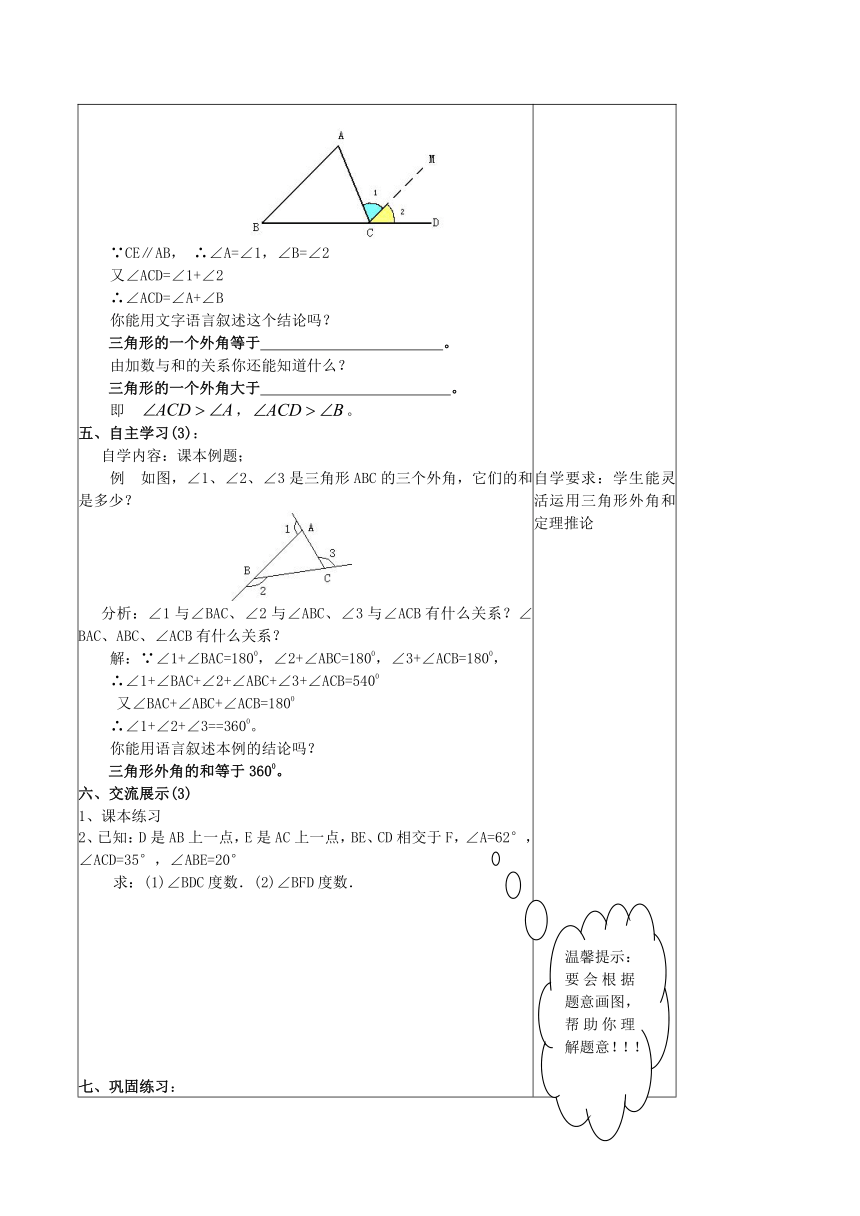
一、自主学习(1):自学内容:教材 “探究”上.二、交流展示(1):1、三角形外角的定义:________________________________2、外角的特征有三:(1)顶点在___________上.(2)一条边是______________.(3)另一条边是__________________.3、画出一个三角形,并画出它的所有外角。4、下列图中,∠1、∠2、∠3哪些是△ABC的外角?三、自主学习(2):自学内容:课本探究前。四、交流展示(2)容易知道,三角形的外角∠ACD与相邻的内角∠ACB是邻补角,那与另外两个角有怎样的数量关系呢?如图,这是我们证明三角形内角和定理时画的辅助线,你能就此图说明∠ACD与∠A、∠B的关系吗?∵CE∥AB, ∴∠A=∠1,∠B=∠2又∠ACD=∠1+∠2∴∠ACD=∠A+∠B你能用文字语言叙述这个结论吗?三角形的一个外角等于 。由加数与和的关系你还能知道什么?三角形的一个外角大于 。即 ,。五、自主学习(3):自学内容:课本例题;例 如图,∠1、∠2、∠3是三角形ABC的三个外角,它们的和是多少? 分析:∠1与∠BAC、∠2与∠ABC、∠3与∠ACB有什么关系?∠BAC、ABC、∠ACB有什么关系?解:∵∠1+∠BAC=1800,∠2+∠ABC=1800,∠3+∠ACB=1800,∴∠1+∠BAC+∠2+∠ABC+∠3+∠ACB=5400 又∠BAC+∠ABC+∠ACB=1800∴∠1+∠2+∠3==3600。你能用语言叙述本例的结论吗?三角形外角的和等于3600。六、交流展示(3)1、课本练习2、已知:D是AB上一点,E是AC上一点,BE、CD相交于F,∠A=62°,∠ACD=35°,∠ABE=20°求:(1)∠BDC度数.(2)∠BFD度数.七、巩固练习:1. 一个三角形的两内角分别55°和65°,它的外角不可能是( )A. 115° B. 120° C. 125° D. 130° 2. 已知三角形的一个外角小于与它相邻的内角,那么这个三角形是( )A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 以上三种情况都有可能3. 已知,如图,在△ABC中,D是三角形内一点,求证:∠BDC>∠BAC。八、展示提升1、已知等腰三角形的一个外角是120°,则它是( )A.等腰直角三角形 B.一般的等腰三角形 C.等边三角形 D.等腰钝角三角形2、如果三角形的一个外角和与它不相邻的两个内角的和为180°,那么与这个外角相邻的内角的度数为( )A. 30° B. 60° C. 90° D. 120° 3、 已知三角形的三个外角的度数比为2∶3∶4,则它的最大内角的度数为( ).A. 90° B. 110° C. 100° D. 120° 4、如图,下列说法错误的是( )A、∠B >∠ACDB、∠B+∠ACB =180°-∠AC、∠B+∠ACB <180°D、∠HEC >∠B5、若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( ).A、直角三角形 B、锐角三角形 C、钝角三角形 D、无法确定6、如图,若∠A=100°,∠B=45°,∠C=38°,则∠DFE等于( )A. 120° B. 115° C. 110° D. 105° 7、如图,∠1=______.8、如图,则∠1=______,∠2=______,∠3=______, 自学要求:学生理解三角形外角和定理推论自学要求:学生能灵活运用三角形外角和定理推论 相信自己,你是最棒的!
3
自学要求:学生理解三角形外角的概念。
温馨提示:要会根据题意画图,帮助你理解题意!!!
【学习目标】 1、知识与技能: 掌握三角形内角和定理的两个推论,并会应用.。2、过程与方法:总结知识内容,使之条理化,加深理解和记忆,养成良好的学习习惯。重点:三角形内角和定理推论的应用.难点:三角形外角的概念.真正理解推论,并能灵活运用.
学习过程 学法指导
一、自主学习(1):自学内容:教材 “探究”上.二、交流展示(1):1、三角形外角的定义:________________________________2、外角的特征有三:(1)顶点在___________上.(2)一条边是______________.(3)另一条边是__________________.3、画出一个三角形,并画出它的所有外角。4、下列图中,∠1、∠2、∠3哪些是△ABC的外角?三、自主学习(2):自学内容:课本探究前。四、交流展示(2)容易知道,三角形的外角∠ACD与相邻的内角∠ACB是邻补角,那与另外两个角有怎样的数量关系呢?如图,这是我们证明三角形内角和定理时画的辅助线,你能就此图说明∠ACD与∠A、∠B的关系吗?∵CE∥AB, ∴∠A=∠1,∠B=∠2又∠ACD=∠1+∠2∴∠ACD=∠A+∠B你能用文字语言叙述这个结论吗?三角形的一个外角等于 。由加数与和的关系你还能知道什么?三角形的一个外角大于 。即 ,。五、自主学习(3):自学内容:课本例题;例 如图,∠1、∠2、∠3是三角形ABC的三个外角,它们的和是多少? 分析:∠1与∠BAC、∠2与∠ABC、∠3与∠ACB有什么关系?∠BAC、ABC、∠ACB有什么关系?解:∵∠1+∠BAC=1800,∠2+∠ABC=1800,∠3+∠ACB=1800,∴∠1+∠BAC+∠2+∠ABC+∠3+∠ACB=5400 又∠BAC+∠ABC+∠ACB=1800∴∠1+∠2+∠3==3600。你能用语言叙述本例的结论吗?三角形外角的和等于3600。六、交流展示(3)1、课本练习2、已知:D是AB上一点,E是AC上一点,BE、CD相交于F,∠A=62°,∠ACD=35°,∠ABE=20°求:(1)∠BDC度数.(2)∠BFD度数.七、巩固练习:1. 一个三角形的两内角分别55°和65°,它的外角不可能是( )A. 115° B. 120° C. 125° D. 130° 2. 已知三角形的一个外角小于与它相邻的内角,那么这个三角形是( )A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 以上三种情况都有可能3. 已知,如图,在△ABC中,D是三角形内一点,求证:∠BDC>∠BAC。八、展示提升1、已知等腰三角形的一个外角是120°,则它是( )A.等腰直角三角形 B.一般的等腰三角形 C.等边三角形 D.等腰钝角三角形2、如果三角形的一个外角和与它不相邻的两个内角的和为180°,那么与这个外角相邻的内角的度数为( )A. 30° B. 60° C. 90° D. 120° 3、 已知三角形的三个外角的度数比为2∶3∶4,则它的最大内角的度数为( ).A. 90° B. 110° C. 100° D. 120° 4、如图,下列说法错误的是( )A、∠B >∠ACDB、∠B+∠ACB =180°-∠AC、∠B+∠ACB <180°D、∠HEC >∠B5、若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( ).A、直角三角形 B、锐角三角形 C、钝角三角形 D、无法确定6、如图,若∠A=100°,∠B=45°,∠C=38°,则∠DFE等于( )A. 120° B. 115° C. 110° D. 105° 7、如图,∠1=______.8、如图,则∠1=______,∠2=______,∠3=______, 自学要求:学生理解三角形外角和定理推论自学要求:学生能灵活运用三角形外角和定理推论 相信自己,你是最棒的!
3
自学要求:学生理解三角形外角的概念。
温馨提示:要会根据题意画图,帮助你理解题意!!!
