九年级数学上册第24章《圆》综合测试题(Word版含答案)
文档属性
| 名称 | 九年级数学上册第24章《圆》综合测试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 956.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-12 00:00:00 | ||
图片预览

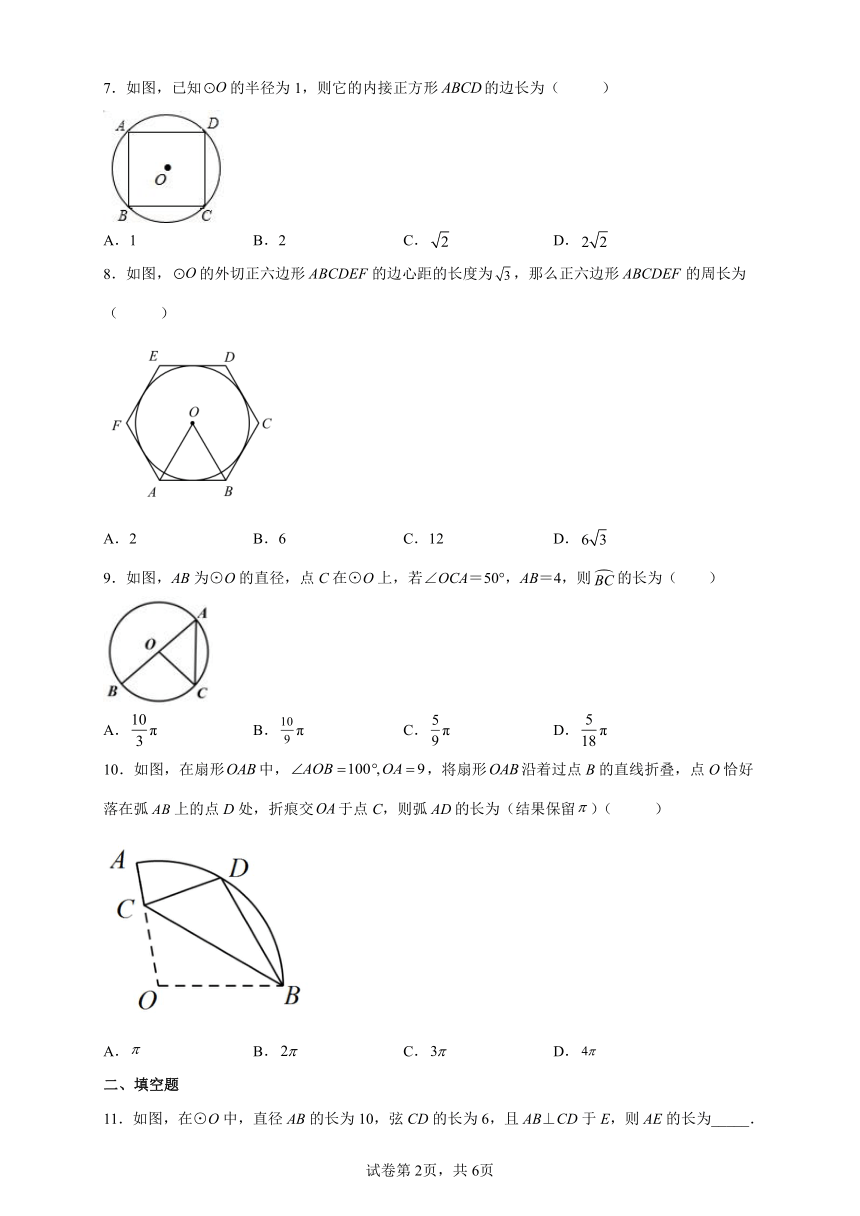
文档简介
2022-2023学年人教版九年级数学上册
第24章《圆》综合测试题
一、单选题
1.已知⊙O中最长的弦为10,则⊙O的半径是( )
A.10 B.20 C.5 D.15
2.下列说法,其中正确的有( )
①过圆心的线段是直径
②圆上的一条弧和经过这条弧的端点的两条半径组成的图形叫做扇形
③大于半圆的弧叫做劣弧
④圆心相同,半径不等的圆叫做同心圆
A.1个 B.2个 C.3个 D.4个
3.如图,已知A,B,C,D四点都在⊙O上,则⊙O中的弦的条数为( )
A.2 B.3 C.4 D.5
4.圆的一条弦把圆分为度数比为的两条弧,则弦心距与弦长的比为( )
A. B. C. D.
5.如图,AB是⊙O的直径,点C、D在⊙O上,且点C、D在AB的异侧,连结AD、OD、OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
A.70° B.60° C.50° D.40°
6.若的半径是4,点A在内,则OA的长可能是( )
A.2 B.4 C.6 D.8
7.如图,已知的半径为1,则它的内接正方形的边长为( )
A.1 B.2 C. D.
8.如图,的外切正六边形的边心距的长度为,那么正六边形的周长为( )
A.2 B.6 C.12 D.
9.如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则的长为( )
A.π B.π C.π D.π
10.如图,在扇形中,,将扇形沿着过点B的直线折叠,点O恰好落在弧上的点D处,折痕交于点C,则弧的长为(结果保留)( )
A. B. C. D.
二、填空题
11.如图,在⊙O中,直径AB的长为10,弦CD的长为6,且AB⊥CD于E,则AE的长为_____.
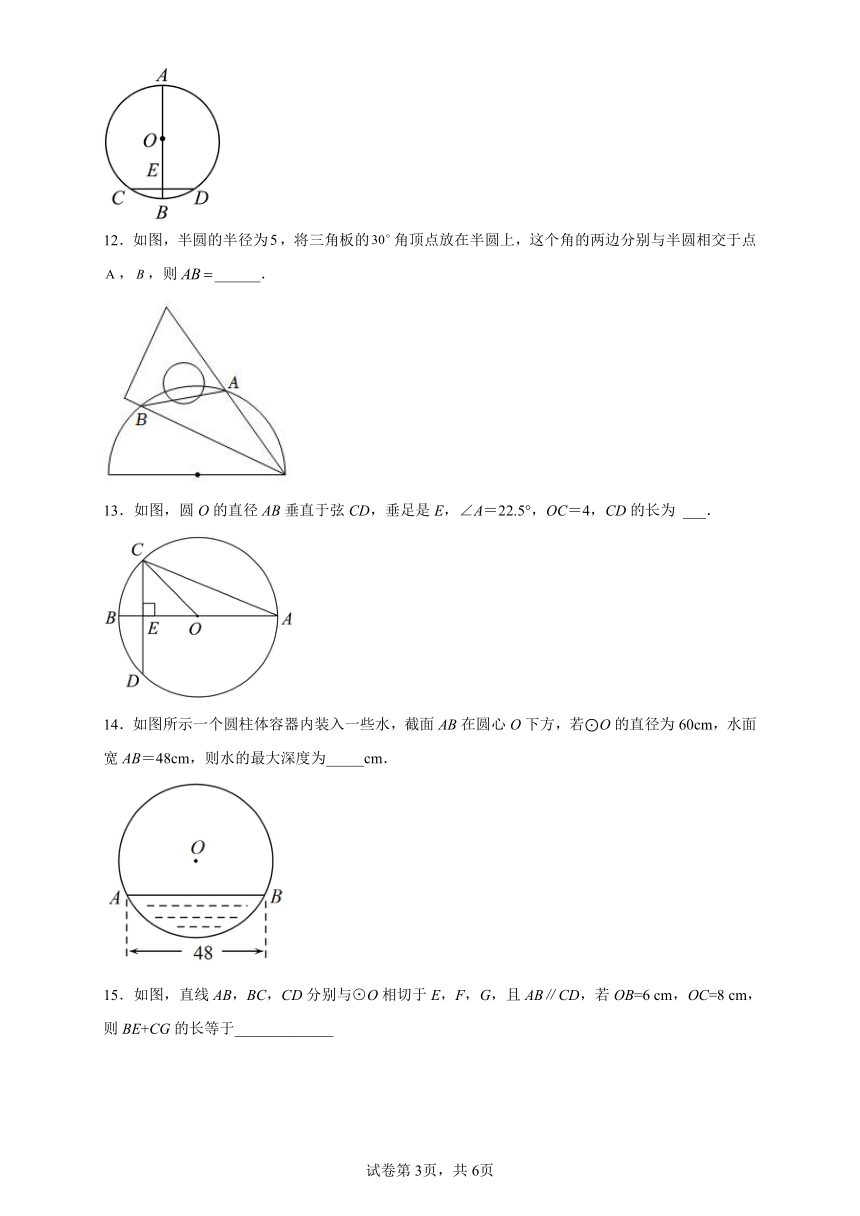
12.如图,半圆的半径为,将三角板的角顶点放在半圆上,这个角的两边分别与半圆相交于点,,则______.
13.如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为 ___.
14.如图所示一个圆柱体容器内装入一些水,截面AB在圆心O下方,若⊙O的直径为60cm,水面宽AB=48cm,则水的最大深度为_____cm.
15.如图,直线AB,BC,CD分别与⊙O相切于E,F,G,且AB∥CD,若OB=6 cm,OC=8 cm,则BE+CG的长等于_____________
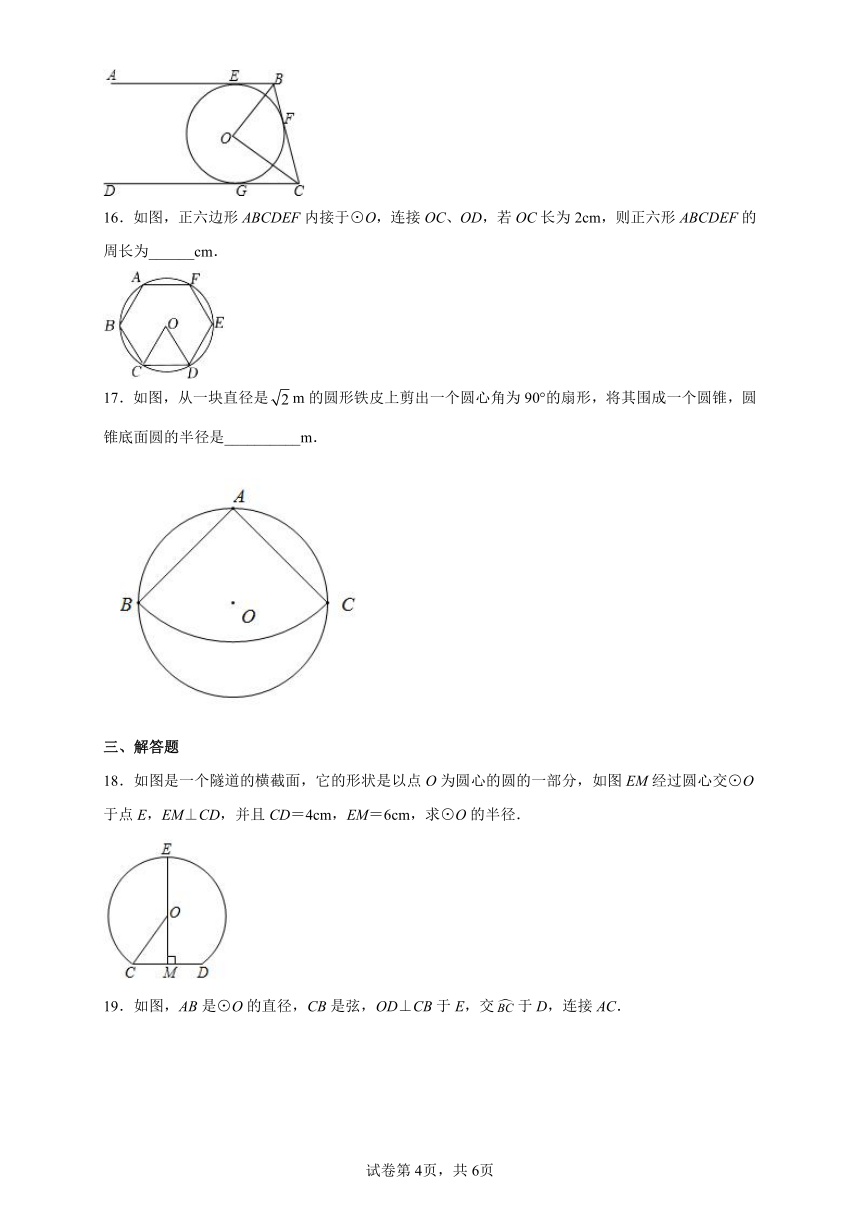
16.如图,正六边形ABCDEF内接于⊙O,连接OC、OD,若OC长为2cm,则正六形ABCDEF的周长为______cm.
17.如图,从一块直径是m的圆形铁皮上剪出一个圆心角为90°的扇形,将其围成一个圆锥,圆锥底面圆的半径是__________m.
三、解答题
18.如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,如图EM经过圆心交⊙O于点E,EM⊥CD,并且CD=4cm,EM=6cm,求⊙O的半径.
19.如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交于D,连接AC.
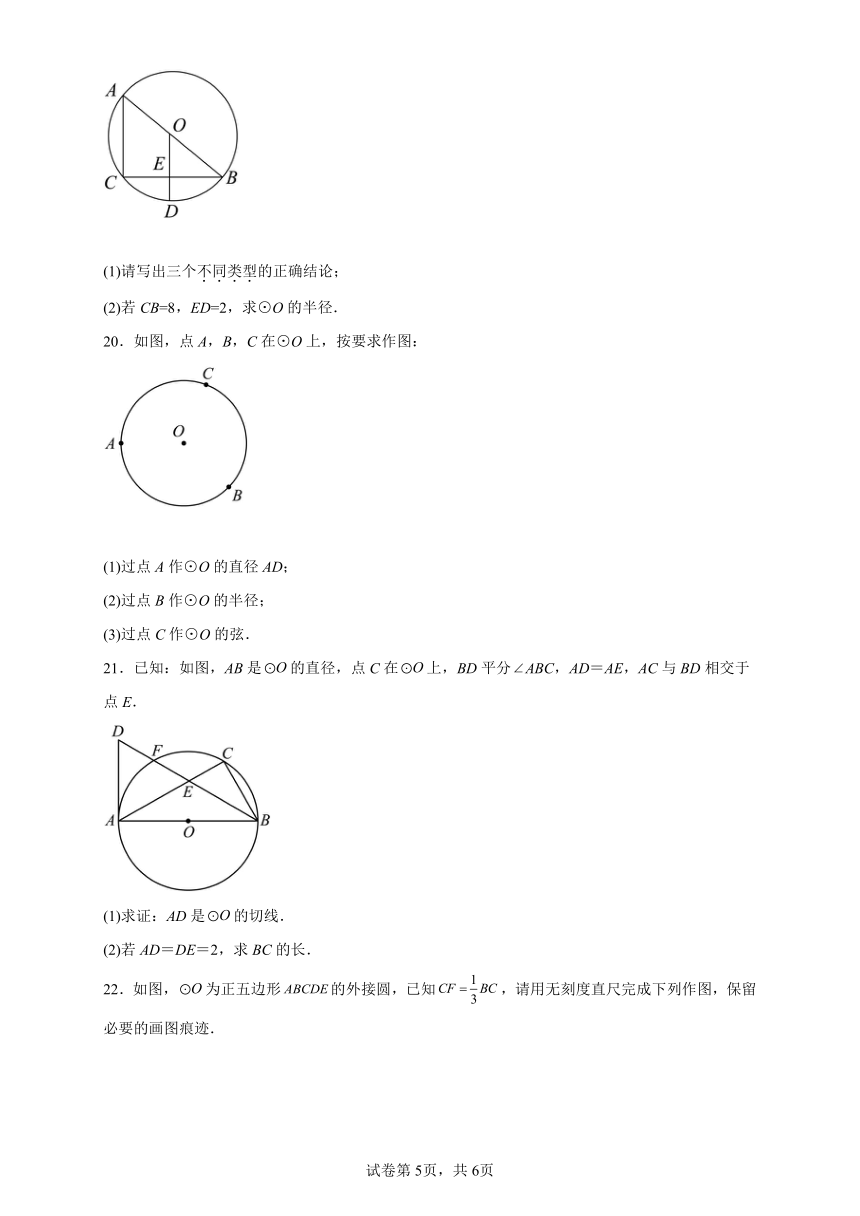
(1)请写出三个不同类型的正确结论;
(2)若CB=8,ED=2,求⊙O的半径.
20.如图,点A,B,C在⊙O上,按要求作图:
(1)过点A作⊙O的直径AD;
(2)过点B作⊙O的半径;
(3)过点C作⊙O的弦.
21.已知:如图,AB是的直径,点C在上,BD平分ABC,AD=AE,AC与BD相交于点E.
(1)求证:AD是的切线.
(2)若AD=DE=2,求BC的长.
22.如图,为正五边形的外接圆,已知,请用无刻度直尺完成下列作图,保留必要的画图痕迹.
(1)在图1中的边上求作点,使;
(2)在图2中的边上求作点,使.
23.如图,点A,B,C在直径为2的⊙O上,∠BAC=45°.
(1)求弧BC的长度;
(2)求图中阴影部分的面积.(结果中保留π)
24.如图,中,,,过点,,的弧的半径为,点在上.,切线交的延长线于点.
(1)求的长;
(2)求的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
∵圆当中最长的弦是直径,
∴直径为10,
∴半径为.
故选:C
2.B
解:①过圆心的弦是直径,故该项错误;
②由一条弧和经过这条弧的两个端点的两条半径组成的图形叫做扇形,故该项正确;
③小于半圆的弧叫做劣弧,故该项错误;
④圆心相同,半径不等的圆叫做同心圆,故该项正确.
故选:B.
3.B
解:根据弦的定义可知,AB、CD和BD都是圆的弦,所以⊙O中的弦的条数为3,
故选:B.
4.D
∵弦AB把⊙O分成度数比为1:3两条弧,
∴弦所对的圆心角∠AOB=,
∴△AOB是等腰直角三角形,
过点O做OC⊥AB于C,
∴,
∴弦心距与弦长的比为1:2.
故选:D.
5.D
解:∵AD∥OC,
∴∠AOC=∠DAO=70°,
又∵OD=OA,
∴∠ADO=∠DAO=70°,
∴∠AOD=180-70°-70°=40°.
故选:D.
6.A
的半径为4,点A在内,
∴OA<4;
∵2<4;
∴2符合;
故选:A.
7.C
连接OB、OC,如图所示,
∵的半径为1,四边形正方形,
∴OB=OC=1,∠BOC=90°,
∴,
故选C.
8.C
解:如图,过点O作OG⊥AB,垂足为G,
由题意可得:OG=,
在正六边形ABCDEF中,∠AOB==60°,OA=OB,
∴△OAB是等边三角形,
∴AB=OA==2,
∴正六边形ABCDEF的周长为2×6=12,
故选:C.
9.B
解:∵∠OCA=50°,OA=OC,
∴∠A=50°,
∴∠BOC=2∠A=100°,
∵AB=4,
∴BO=2,
∴的长为:π.
故选:B.
10.B
解:如图,连接OD.
根据折叠的性质知,OB=DB.
又∵OD=OB,
∴OD=OB=DB,即△ODB是等边三角形,
∴∠DOB=60°.
∵∠AOB=100°,
∴∠AOD=∠AOB-∠DOB=40°,
∴的长为 =2π.
故选:B.
11.9
解:如图,连接,
的直径的长为10,
,
弦的长为6,且于,
,
在中,,
则,
故答案为:9.
12.
解:如图,设点为圆心,连接,,
∴,
∵,
∴,
∴为等边三角形,
∴.
故答案为:.
13.4
解:∵∠A=22.5°,
∴∠BOC=2∠A=45°,
∵⊙O的直径AB垂直于弦CD,
∴CE=DE,△OCE为等腰直角三角形,
∴CEOC=2,
∴CD=2CE=4.
故答案为4.
14.12
解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,
∴BD=AB=×48=24(cm),
∵⊙O的直径为60cm,
∴OB=OC=30cm,
在Rt△OBD中,OD===18(cm),
∴CD=OC﹣OD=30﹣18=12(cm),
即水的最大深度为12cm,
故答案为:12.
15.10cm
解:∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵直线AB,BC,CD分别与⊙O相切于E,F,G,
∴∠OBC=∠ABC,∠OCB=∠BCD,BE=BF,CG=CF,
∴∠OBC+∠OCB=(∠ABC+∠BCD)=90°,
∴∠BOC=90°,
在Rt△BOC中,
BC==10,
∴BE+CG=10(cm).
故答案为:10cm.
16.12
解:∵多边形ABCDEF为正六边形,
∴∠COD=360°×=60°,
∵OC=OD,
∴△OCD是等边三角形,
∵OC长为2cm,
∴CD=2cm,
∴正六形ABCDEF的周长为2×6=12(cm),
故答案为:12.
17.
解:连接BC、AO,
∵⊙O的直径为m,
∴半径是m,
∵AB=AC,OB=OC,
∴BC⊥AO,AO=BO=m,
在Rt△ABO中,AB=m,
∴圆锥底面圆的弧长,
设圆锥底面圆的半径是r,
则,
∴m,
故答案为:.
18.
解:连接OC,
∵EM过圆心,EM⊥CD,
∴CM=CD,
∵CD=4cm,
∴CM=2cm,
设圆的半径是xcm,
在Rt△COM中,OC2=CM2+OM2,
即:x2=22+(6﹣x)2,
解得:x=,
∴圆的半径长是cm.
19
(1)不同类型的正确结论有:①BE=CE;②;③∠BED=90°.证明如下:∵CB是弦,OD⊥CB于E,∴BE=CE,,∠BED=90°.
(2)∵OD⊥CB∴BE=CE==4设半径等于R,则OE=OD-DE=R-2在Rt△OEB中,由勾股定理得, 即解得R=5∴⊙O的半径为5.
20.
(1)如图所示,作射线,交于点,则线段即为的直径;
(2)如图所示,连接,线段即为所求;
(3)如图所示,连接,线段即为所求的一条弦(答案不唯一).
21
(1)∵AB是的直径,∴C=90°,∴CBE+CEB=90°,∵BD平分ABC,∴CBD=ABD,∵AD=AE,∴D=AED,∵CEB=DEA,∴ABD+D=CBE+CEB=90°,即BAD=90°,∴AD是⊙O的切线 ,
(2)连接AF,如图,∵AB是的直径,∴AFB=90°,即, ∵AD=DE=2,∴DF=DE=1, 在中,AD=2,DF=1,∴AF== , ∵ DBA+D=EAB+ DAE = 90°,D=DAE=60°,∴DBA=EAB,∴AE=BE, 又AFE=C=90°,AEF=CEB,∴△AEF≌△BEC(AAS), ∴BC=AF=.
22.
(1)
连接AO并延长 与CD相交,连接EF交AO延长线于M,连接BM交DE于点G,则点G为所求作,如图1所示;
理由:
∵⊙O为正五边形的外接圆,
∴直线AO是正五边形ABCDE的一条对称轴,点B与点E、点C与点D分别是一对对称点.
∵点M在直线AO上,
∴射线BM与射线EF关于直线AO对称,从而点F与点G关于直线AO对称,
∴CF与DG关于直线AO对称.
∴DG=CF.
(2)
在(1)的基础上,连接BO并延长与DE相交,连接AG交BO延长线于N,连接CN,如图2所示;
23.
(1)如图,连接OB,OC.∵∠BOC=2∠A,∠A=45°,∴∠BOC=90°,∵⊙O的直径为2,∴OB=OC=1,∴;
(2)∵∠BOC=90°,∴△BOC是直角三角形,∵⊙O的直径为2,∴OB=OC=1,∴△BOC的面积为,∵,即S阴=S扇形OBC﹣S△OBC=.
24
(1)解:如图,连接,∵,∴,∵过点,,的弧的半径为,∴,∴的长为,∴的长为.
(2)如图,连接,∵,,∴,∵,,∴,∴,∵,∴,∴,∵,∴是等边三角形,∴,∵是的切线,∴,∴,∴.∴的度数为.
答案第1页,共2页
答案第1页,共2页
第24章《圆》综合测试题
一、单选题
1.已知⊙O中最长的弦为10,则⊙O的半径是( )
A.10 B.20 C.5 D.15
2.下列说法,其中正确的有( )
①过圆心的线段是直径
②圆上的一条弧和经过这条弧的端点的两条半径组成的图形叫做扇形
③大于半圆的弧叫做劣弧
④圆心相同,半径不等的圆叫做同心圆
A.1个 B.2个 C.3个 D.4个
3.如图,已知A,B,C,D四点都在⊙O上,则⊙O中的弦的条数为( )
A.2 B.3 C.4 D.5
4.圆的一条弦把圆分为度数比为的两条弧,则弦心距与弦长的比为( )
A. B. C. D.
5.如图,AB是⊙O的直径,点C、D在⊙O上,且点C、D在AB的异侧,连结AD、OD、OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
A.70° B.60° C.50° D.40°
6.若的半径是4,点A在内,则OA的长可能是( )
A.2 B.4 C.6 D.8
7.如图,已知的半径为1,则它的内接正方形的边长为( )
A.1 B.2 C. D.
8.如图,的外切正六边形的边心距的长度为,那么正六边形的周长为( )
A.2 B.6 C.12 D.
9.如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则的长为( )
A.π B.π C.π D.π
10.如图,在扇形中,,将扇形沿着过点B的直线折叠,点O恰好落在弧上的点D处,折痕交于点C,则弧的长为(结果保留)( )
A. B. C. D.
二、填空题
11.如图,在⊙O中,直径AB的长为10,弦CD的长为6,且AB⊥CD于E,则AE的长为_____.
12.如图,半圆的半径为,将三角板的角顶点放在半圆上,这个角的两边分别与半圆相交于点,,则______.
13.如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为 ___.
14.如图所示一个圆柱体容器内装入一些水,截面AB在圆心O下方,若⊙O的直径为60cm,水面宽AB=48cm,则水的最大深度为_____cm.
15.如图,直线AB,BC,CD分别与⊙O相切于E,F,G,且AB∥CD,若OB=6 cm,OC=8 cm,则BE+CG的长等于_____________
16.如图,正六边形ABCDEF内接于⊙O,连接OC、OD,若OC长为2cm,则正六形ABCDEF的周长为______cm.
17.如图,从一块直径是m的圆形铁皮上剪出一个圆心角为90°的扇形,将其围成一个圆锥,圆锥底面圆的半径是__________m.
三、解答题
18.如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,如图EM经过圆心交⊙O于点E,EM⊥CD,并且CD=4cm,EM=6cm,求⊙O的半径.
19.如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交于D,连接AC.
(1)请写出三个不同类型的正确结论;
(2)若CB=8,ED=2,求⊙O的半径.
20.如图,点A,B,C在⊙O上,按要求作图:
(1)过点A作⊙O的直径AD;
(2)过点B作⊙O的半径;
(3)过点C作⊙O的弦.
21.已知:如图,AB是的直径,点C在上,BD平分ABC,AD=AE,AC与BD相交于点E.
(1)求证:AD是的切线.
(2)若AD=DE=2,求BC的长.
22.如图,为正五边形的外接圆,已知,请用无刻度直尺完成下列作图,保留必要的画图痕迹.
(1)在图1中的边上求作点,使;
(2)在图2中的边上求作点,使.
23.如图,点A,B,C在直径为2的⊙O上,∠BAC=45°.
(1)求弧BC的长度;
(2)求图中阴影部分的面积.(结果中保留π)
24.如图,中,,,过点,,的弧的半径为,点在上.,切线交的延长线于点.
(1)求的长;
(2)求的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
∵圆当中最长的弦是直径,
∴直径为10,
∴半径为.
故选:C
2.B
解:①过圆心的弦是直径,故该项错误;
②由一条弧和经过这条弧的两个端点的两条半径组成的图形叫做扇形,故该项正确;
③小于半圆的弧叫做劣弧,故该项错误;
④圆心相同,半径不等的圆叫做同心圆,故该项正确.
故选:B.
3.B
解:根据弦的定义可知,AB、CD和BD都是圆的弦,所以⊙O中的弦的条数为3,
故选:B.
4.D
∵弦AB把⊙O分成度数比为1:3两条弧,
∴弦所对的圆心角∠AOB=,
∴△AOB是等腰直角三角形,
过点O做OC⊥AB于C,
∴,
∴弦心距与弦长的比为1:2.
故选:D.
5.D
解:∵AD∥OC,
∴∠AOC=∠DAO=70°,
又∵OD=OA,
∴∠ADO=∠DAO=70°,
∴∠AOD=180-70°-70°=40°.
故选:D.
6.A
的半径为4,点A在内,
∴OA<4;
∵2<4;
∴2符合;
故选:A.
7.C
连接OB、OC,如图所示,
∵的半径为1,四边形正方形,
∴OB=OC=1,∠BOC=90°,
∴,
故选C.
8.C
解:如图,过点O作OG⊥AB,垂足为G,
由题意可得:OG=,
在正六边形ABCDEF中,∠AOB==60°,OA=OB,
∴△OAB是等边三角形,
∴AB=OA==2,
∴正六边形ABCDEF的周长为2×6=12,
故选:C.
9.B
解:∵∠OCA=50°,OA=OC,
∴∠A=50°,
∴∠BOC=2∠A=100°,
∵AB=4,
∴BO=2,
∴的长为:π.
故选:B.
10.B
解:如图,连接OD.
根据折叠的性质知,OB=DB.
又∵OD=OB,
∴OD=OB=DB,即△ODB是等边三角形,
∴∠DOB=60°.
∵∠AOB=100°,
∴∠AOD=∠AOB-∠DOB=40°,
∴的长为 =2π.
故选:B.
11.9
解:如图,连接,
的直径的长为10,
,
弦的长为6,且于,
,
在中,,
则,
故答案为:9.
12.
解:如图,设点为圆心,连接,,
∴,
∵,
∴,
∴为等边三角形,
∴.
故答案为:.
13.4
解:∵∠A=22.5°,
∴∠BOC=2∠A=45°,
∵⊙O的直径AB垂直于弦CD,
∴CE=DE,△OCE为等腰直角三角形,
∴CEOC=2,
∴CD=2CE=4.
故答案为4.
14.12
解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,
∴BD=AB=×48=24(cm),
∵⊙O的直径为60cm,
∴OB=OC=30cm,
在Rt△OBD中,OD===18(cm),
∴CD=OC﹣OD=30﹣18=12(cm),
即水的最大深度为12cm,
故答案为:12.
15.10cm
解:∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵直线AB,BC,CD分别与⊙O相切于E,F,G,
∴∠OBC=∠ABC,∠OCB=∠BCD,BE=BF,CG=CF,
∴∠OBC+∠OCB=(∠ABC+∠BCD)=90°,
∴∠BOC=90°,
在Rt△BOC中,
BC==10,
∴BE+CG=10(cm).
故答案为:10cm.
16.12
解:∵多边形ABCDEF为正六边形,
∴∠COD=360°×=60°,
∵OC=OD,
∴△OCD是等边三角形,
∵OC长为2cm,
∴CD=2cm,
∴正六形ABCDEF的周长为2×6=12(cm),
故答案为:12.
17.
解:连接BC、AO,
∵⊙O的直径为m,
∴半径是m,
∵AB=AC,OB=OC,
∴BC⊥AO,AO=BO=m,
在Rt△ABO中,AB=m,
∴圆锥底面圆的弧长,
设圆锥底面圆的半径是r,
则,
∴m,
故答案为:.
18.
解:连接OC,
∵EM过圆心,EM⊥CD,
∴CM=CD,
∵CD=4cm,
∴CM=2cm,
设圆的半径是xcm,
在Rt△COM中,OC2=CM2+OM2,
即:x2=22+(6﹣x)2,
解得:x=,
∴圆的半径长是cm.
19
(1)不同类型的正确结论有:①BE=CE;②;③∠BED=90°.证明如下:∵CB是弦,OD⊥CB于E,∴BE=CE,,∠BED=90°.
(2)∵OD⊥CB∴BE=CE==4设半径等于R,则OE=OD-DE=R-2在Rt△OEB中,由勾股定理得, 即解得R=5∴⊙O的半径为5.
20.
(1)如图所示,作射线,交于点,则线段即为的直径;
(2)如图所示,连接,线段即为所求;
(3)如图所示,连接,线段即为所求的一条弦(答案不唯一).
21
(1)∵AB是的直径,∴C=90°,∴CBE+CEB=90°,∵BD平分ABC,∴CBD=ABD,∵AD=AE,∴D=AED,∵CEB=DEA,∴ABD+D=CBE+CEB=90°,即BAD=90°,∴AD是⊙O的切线 ,
(2)连接AF,如图,∵AB是的直径,∴AFB=90°,即, ∵AD=DE=2,∴DF=DE=1, 在中,AD=2,DF=1,∴AF== , ∵ DBA+D=EAB+ DAE = 90°,D=DAE=60°,∴DBA=EAB,∴AE=BE, 又AFE=C=90°,AEF=CEB,∴△AEF≌△BEC(AAS), ∴BC=AF=.
22.
(1)
连接AO并延长 与CD相交,连接EF交AO延长线于M,连接BM交DE于点G,则点G为所求作,如图1所示;
理由:
∵⊙O为正五边形的外接圆,
∴直线AO是正五边形ABCDE的一条对称轴,点B与点E、点C与点D分别是一对对称点.
∵点M在直线AO上,
∴射线BM与射线EF关于直线AO对称,从而点F与点G关于直线AO对称,
∴CF与DG关于直线AO对称.
∴DG=CF.
(2)
在(1)的基础上,连接BO并延长与DE相交,连接AG交BO延长线于N,连接CN,如图2所示;
23.
(1)如图,连接OB,OC.∵∠BOC=2∠A,∠A=45°,∴∠BOC=90°,∵⊙O的直径为2,∴OB=OC=1,∴;
(2)∵∠BOC=90°,∴△BOC是直角三角形,∵⊙O的直径为2,∴OB=OC=1,∴△BOC的面积为,∵,即S阴=S扇形OBC﹣S△OBC=.
24
(1)解:如图,连接,∵,∴,∵过点,,的弧的半径为,∴,∴的长为,∴的长为.
(2)如图,连接,∵,,∴,∵,,∴,∴,∵,∴,∴,∵,∴是等边三角形,∴,∵是的切线,∴,∴,∴.∴的度数为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
