2022-2023学年冀教版九年级数学上册28.2过三点的圆课件(共15张PPT)
文档属性
| 名称 | 2022-2023学年冀教版九年级数学上册28.2过三点的圆课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 861.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-12 19:53:25 | ||
图片预览





文档简介
(共15张PPT)
28.2 过三点的圆
学习目标
1.理解不在同一直线上的三个点确定一个圆及其运用.(重点)
2.了解三角形的外接圆和三角形外心的概念.
1.过不在同一直线上的三个点作圆
问题1:平面上有一点A,经过已知A点的圆有几个?圆心在哪里?
●O
●A
●O
●O
●O
●O
圆心和半径不确定,能画出无数个圆,圆心为点A以外任意一点,半径为这点与点A之间的距离.
知识讲解
r2
r1
·
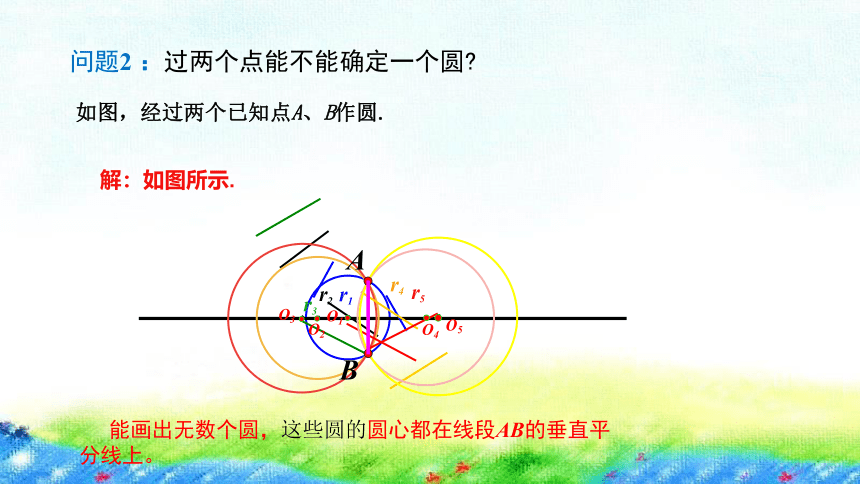
问题2 :过两个点能不能确定一个圆
如图,经过两个已知点A、B作圆.
·
O2
O1
O3
·
·
O4
r4
O5
·
r5
B
A
解:如图所示.
能画出无数个圆,这些圆的圆心都在线段AB的垂直平分线上。
r3
问题3:经过不在同一条直线上的三点A、B、C能不能作圆?如果能,如何确定所作的圆心?
∴点O就是所求的圆心.
作法:
1、连接AB、BC;
2、分别作AB、BC的垂直
平分线,两线交于O.
A
C
B
·
r
o
结论 :
不在同一条直线上的三点确定 个圆.
一
问题4.如果平面上三点A,B,C在一条直线上,经过A,B,C的圆是否存在 为什么
(不存在,因为线段AB,BC的垂直平分线平行,没有交点)
三角形的外接圆和外心
2.
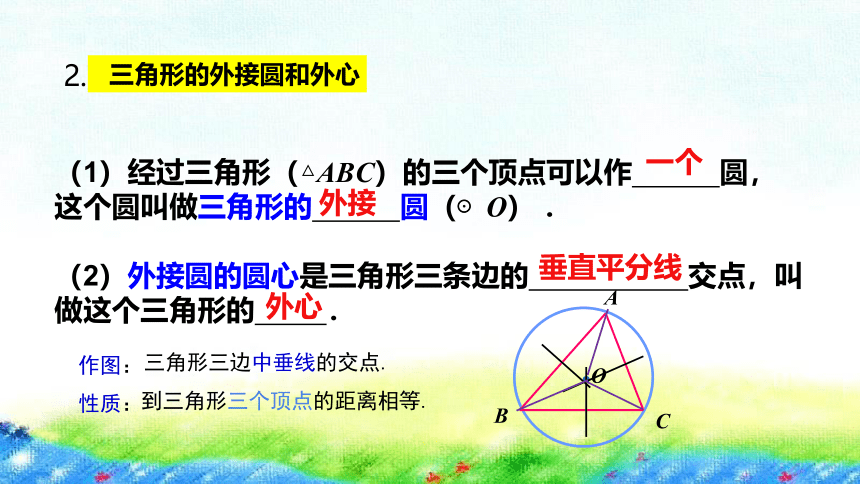
(1)经过三角形(△ABC)的三个顶点可以作 圆,这个圆叫做三角形的 圆(⊙O) .
(2)外接圆的圆心是三角形三条边的 交点,叫做这个三角形的 .
一个
外接
垂直平分线
外心
到三角形三个顶点的距离相等.
●O
A
B
C
作图:
三角形三边中垂线的交点.
性质:
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
1.锐角三角形的外心位于三角形内,
2.直角三角形的外心位于直角三角形斜边的中点处,
3.钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
用尺规作过三角形三个顶点的圆.
已知:如图所示,△ABC.
求作:☉O,使它过三点A,B,C.
作法:如图所示.
(1)分别作线段AB和BC的垂直平分线l1和l2.设l1与l2相交于点O.
l1
l2
(2)以点O为圆心,OA为半径画圆.
☉O即为所求.
O
3.三角形的外接圆的作法
1.下列说法是否正确?
(1)任意的一个三角形一定有一个外接圆( )
(2)任意一个圆有且只有一个内接三角形( )
(3)经过三点一定可以确定一个圆( )
(4)三角形的外心到三角形各顶点的距离相等( )
√
×
×
√
随堂训练
2.如图所示,点A,B,C在同一条直线上,点D在直线AB外,过这4个点中的任意3个点,能画圆的个数是 ( )
A.1 B.2 C.3 D.4
C
3.已知△ABC的一边长为10,另两边长分别是方程-14x+48=0的两个根,若用一圆形纸片将此三角形完全覆盖,则该圆形纸片的最小半径是 .
5
解析:解方程x2-14x+48=0,得x1=8,x2=6,即△ABC的三条边长为10,8,6.
∵102=82+62,∴△ABC是直角三角形,圆形纸片将此三角形完全覆盖的最小圆为三角形的外接圆,那么圆形纸片的最小直径为直角三角形的斜边,即为10,那么半径为5.
4.已知Rt△ABC的两直角边为a和b,且a,b是方程x2-3x+1=0的两根,求Rt△ABC的外接圆面积.
5.如图,是一块圆形镜片破碎后的部分残片,试找出它的圆心.
A
B
C
O
圆心一定在弦的垂直平分线上.
课堂小结
作圆
过一点可以作无数个圆
过两点可以作无数个圆
过不在同一直线上的三个点确定一个圆
直角三角形的外心在斜边中点处
注意:过同一直线上的三个点不能作圆
Thank you for listening
感谢聆听
28.2 过三点的圆
学习目标
1.理解不在同一直线上的三个点确定一个圆及其运用.(重点)
2.了解三角形的外接圆和三角形外心的概念.
1.过不在同一直线上的三个点作圆
问题1:平面上有一点A,经过已知A点的圆有几个?圆心在哪里?
●O
●A
●O
●O
●O
●O
圆心和半径不确定,能画出无数个圆,圆心为点A以外任意一点,半径为这点与点A之间的距离.
知识讲解
r2
r1
·
问题2 :过两个点能不能确定一个圆
如图,经过两个已知点A、B作圆.
·
O2
O1
O3
·
·
O4
r4
O5
·
r5
B
A
解:如图所示.
能画出无数个圆,这些圆的圆心都在线段AB的垂直平分线上。
r3
问题3:经过不在同一条直线上的三点A、B、C能不能作圆?如果能,如何确定所作的圆心?
∴点O就是所求的圆心.
作法:
1、连接AB、BC;
2、分别作AB、BC的垂直
平分线,两线交于O.
A
C
B
·
r
o
结论 :
不在同一条直线上的三点确定 个圆.
一
问题4.如果平面上三点A,B,C在一条直线上,经过A,B,C的圆是否存在 为什么
(不存在,因为线段AB,BC的垂直平分线平行,没有交点)
三角形的外接圆和外心
2.
(1)经过三角形(△ABC)的三个顶点可以作 圆,这个圆叫做三角形的 圆(⊙O) .
(2)外接圆的圆心是三角形三条边的 交点,叫做这个三角形的 .
一个
外接
垂直平分线
外心
到三角形三个顶点的距离相等.
●O
A
B
C
作图:
三角形三边中垂线的交点.
性质:
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
1.锐角三角形的外心位于三角形内,
2.直角三角形的外心位于直角三角形斜边的中点处,
3.钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
用尺规作过三角形三个顶点的圆.
已知:如图所示,△ABC.
求作:☉O,使它过三点A,B,C.
作法:如图所示.
(1)分别作线段AB和BC的垂直平分线l1和l2.设l1与l2相交于点O.
l1
l2
(2)以点O为圆心,OA为半径画圆.
☉O即为所求.
O
3.三角形的外接圆的作法
1.下列说法是否正确?
(1)任意的一个三角形一定有一个外接圆( )
(2)任意一个圆有且只有一个内接三角形( )
(3)经过三点一定可以确定一个圆( )
(4)三角形的外心到三角形各顶点的距离相等( )
√
×
×
√
随堂训练
2.如图所示,点A,B,C在同一条直线上,点D在直线AB外,过这4个点中的任意3个点,能画圆的个数是 ( )
A.1 B.2 C.3 D.4
C
3.已知△ABC的一边长为10,另两边长分别是方程-14x+48=0的两个根,若用一圆形纸片将此三角形完全覆盖,则该圆形纸片的最小半径是 .
5
解析:解方程x2-14x+48=0,得x1=8,x2=6,即△ABC的三条边长为10,8,6.
∵102=82+62,∴△ABC是直角三角形,圆形纸片将此三角形完全覆盖的最小圆为三角形的外接圆,那么圆形纸片的最小直径为直角三角形的斜边,即为10,那么半径为5.
4.已知Rt△ABC的两直角边为a和b,且a,b是方程x2-3x+1=0的两根,求Rt△ABC的外接圆面积.
5.如图,是一块圆形镜片破碎后的部分残片,试找出它的圆心.
A
B
C
O
圆心一定在弦的垂直平分线上.
课堂小结
作圆
过一点可以作无数个圆
过两点可以作无数个圆
过不在同一直线上的三个点确定一个圆
直角三角形的外心在斜边中点处
注意:过同一直线上的三个点不能作圆
Thank you for listening
感谢聆听
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
