2022-2023学年北师大版九年级数学上册4.4探索三角形相似的条件 同步练习题(word版含答案)
文档属性
| 名称 | 2022-2023学年北师大版九年级数学上册4.4探索三角形相似的条件 同步练习题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 378.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-12 21:15:22 | ||
图片预览



文档简介
2022-2023学年北师大版九年级数学上册《4.4探索三角形相似的条件》
同步练习题(附答案)
一.选择题
1.如图,在四边形ABCD中,∠BAC=90°,AB=6,AC=8,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.下列结论错误的是( )
A.四边形AECD的周长是20 B.△ABC∽△FEC
C.∠B+∠ACD=90° D.EF的长为
2.如图,在△ABC中,点D、E分别在边AB、AC上,则在下列四个条件中:①∠AED=∠B;②DE∥BC;③;④AD BC=DE AC,能满足△ADE∽△ACB的条件有( )
A.1个 B.2个 C.3个 D.4个
3.如图,在△ABC中,D是BC的中点,DE⊥BC交AC于E,已知AD=AB,连接BE交AD于F,下列结论:①BE=CE;②∠CAD=∠ABE;③AF=DF;④S△ABF=3S△DEF;⑤△DEF∽△DAE,其中正确的有( )个.
A.5 B.4 C.3 D.2
二.填空题
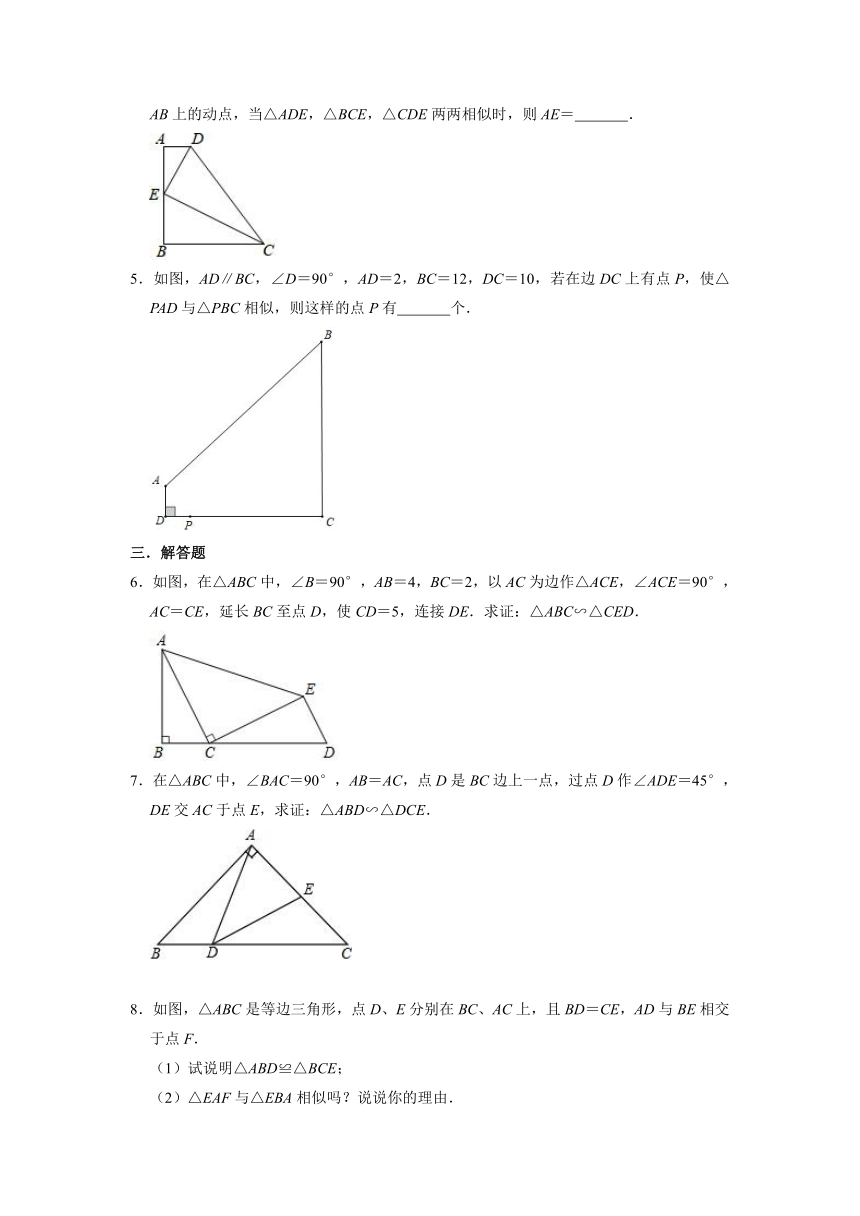
4.如图,在四边形ABCD中,AD∥BC,AD<BC,∠ABC=90°,且AB=3,点E是边AB上的动点,当△ADE,△BCE,△CDE两两相似时,则AE= .
5.如图,AD∥BC,∠D=90°,AD=2,BC=12,DC=10,若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有 个.
三.解答题
6.如图,在△ABC中,∠B=90°,AB=4,BC=2,以AC为边作△ACE,∠ACE=90°,AC=CE,延长BC至点D,使CD=5,连接DE.求证:△ABC∽△CED.
7.在△ABC中,∠BAC=90°,AB=AC,点D是BC边上一点,过点D作∠ADE=45°,DE交AC于点E,求证:△ABD∽△DCE.
8.如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.
(1)试说明△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.
如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F.
(1)求证:△PFA∽△ABE;
(2)当点P在射线AD上运动时,设PA=x,是否存在实数x,使以P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,说明理由.
10.如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且==.
(1)试问:∠BAE与∠CAD相等吗?为什么?
(2)试判断△ABE与△ACD是否相似?并说明理由.
11.如图,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连接AE,BD,设AE交CD于点F.
(1)求证:△ACE≌△DCB;
(2)求证:△ADF∽△BAD.
12.尤秀同学遇到了这样一个问题:如图1所示,已知AF,BE是△ABC的中线,且AF⊥BE,垂足为P,设BC=a,AC=b,AB=c.
求证:a2+b2=5c2
该同学仔细分析后,得到如下解题思路:
先连接EF,利用EF为△ABC的中位线得到△EPF∽△BPA,故,设PF=m,PE=n,用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF中利用勾股定理计算,消去m,n即可得证
(1)请你根据以上解题思路帮尤秀同学写出证明过程.
(2)利用题中的结论,解答下列问题:
在边长为3的菱形ABCD中,O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图2所示,求MG2+MH2的值.
13.如图,在△ABC中,AB=AC=1,BC=,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与AC CD的大小关系;
(2)求∠ABD的度数.
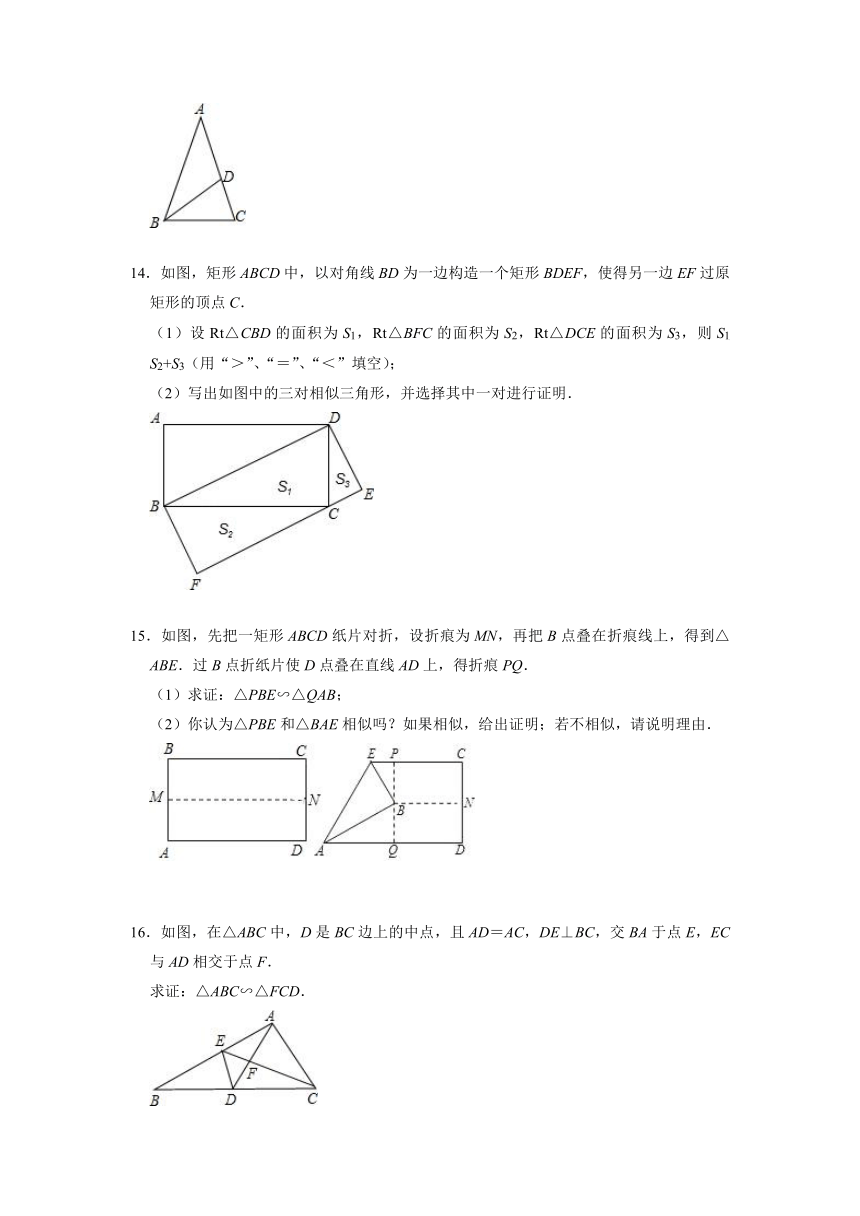
14.如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.
(1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,则S1 S2+S3(用“>”、“=”、“<”填空);
(2)写出如图中的三对相似三角形,并选择其中一对进行证明.
15.如图,先把一矩形ABCD纸片对折,设折痕为MN,再把B点叠在折痕线上,得到△ABE.过B点折纸片使D点叠在直线AD上,得折痕PQ.
(1)求证:△PBE∽△QAB;
(2)你认为△PBE和△BAE相似吗?如果相似,给出证明;若不相似,请说明理由.
16.如图,在△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,交BA于点E,EC与AD相交于点F.
求证:△ABC∽△FCD.
17.已知:在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,E是BC的中点,连接AE、AC.
(1)点F是DC上一点,连接EF,交AC于点O(如图1),求证:△AOE∽△COF;
(2)若点F是DC的中点,连接BD,交AE与点G(如图2),求证:四边形EFDG是菱形.
18.已知:如图,Rt△ABC中,∠BAC=90°,D是AC上一点,∠ABD=∠C,直线EF过点D,与BA的延长线相交于F,且EF⊥BC,垂足为E.
(1)写出图中所有与△ABD相似的三角形;
(2)探索:设,是否存在这样的t值,使得△ADF∽△EDB?说明理由.
19.如图,在矩形ABCD中,点E、F分别在边AD、CD上(F不与C重合),且∠BEF=90°
(1)△ABE与△DEF相似吗?为什么?
(2)当点E位于AD上何处时,△ABE、△BEF、△DEF这三个三角形都相似?
(3)当△ABE、△BEF、△DEF、△CBF这四个三角形都相似时,求及的值.
20.如图,在△ABC中,AB=AC,点D、E分别在BC、AB上,且∠BDE=∠CAD.求证:△ADE∽△ABD.
21.在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,设P、Q两点同时出发,移动时间为t秒.
(1)几秒钟后△PBQ是等腰三角形?
(2)几秒钟后△PQB的面积为5cm2?
(3)几秒钟后,以P、B、Q为顶点的三角形和△ABC相似?
22.王华在学习相似三角形时,在北京市义务教育教科书九年级上册第31页遇到这样一道题,如图1,在△ABC中,P是边AB上的一点,连接CP,要使△ACP∽△ABC,还需要补充的一个条件是 ,或 .
请回答:
(1)王华补充的条件是 ,或 .
(2)请你参考上面的图形和结论,探究,解答下面的问题:
如图2,在△ABC中,∠A=30°,AC2=AB2+AB BC.求∠C的度数.
23.已知:点A(1,3),点B(﹣3,0),点C(1,0)
(1)请在x轴上找一点D,使得△BDA与△BAC相似(不包含全等),并求出点D的坐标;
(2)在(1)的条件下,如果P、Q分别是BA、BD上的动点,连接PQ,设BP=DQ=m,问:是否存在这样的m,使得△BPQ与△BDA相似?如存在,请求出m的值;若不存在,请说明理由.
参考答案
1.解:∵∠BAC=90°,AB=6,AC=8,
∴BC==10,
∵AD∥BC,AE∥DC,
∴四边形AECD是平行四边形,
∵∠BAC=90°,E是BC的中点,
∴AE=CE=BC=5,
∴四边形AECD是菱形,
∴菱形AECD的周长是20,
故A选项正确,不符合题意;
∵四边形AECD是菱形,
∴∠ACB=∠ACD,
∵∠B+∠ACB=90°,
∴∠B+∠ACD=90°,
故C选项正确,不符合题意;
如图,过A作AH⊥BC于点H,
∵S△ABC=BC AH=AB AC,
∴AH==,
∵点E是BC的中点,BC=10,四边形AECD是菱形,
∴CD=CE=5,
∵S AECD=CE AH=CD EF,
∴EF=AH=.
故D选项正确,不符合题意;
在Rt△EFC中,EF=,EC=5,
∴FC==,
在Rt△CAB中,AB=6,AC=8,BC=10,
∵=,=,=,
∴△ABC与△FEC不相似,故B选项错误,符合题意.
故选:B.
2.解:①∠B=∠AED,∠A=∠A,则可判断△ADE∽△ACB,故①符合题意;
②DE∥BC,则△ADE∽△ABC,故②不符合题意,
③,且夹角∠A=∠A,能确定△ADE∽△ACB,故③符合题意;
④由AD BC=DE AC可得=,此时不确定∠ADE=∠ACB,故不能确定△ADE∽△ACB,故④不符合题意,
故选:B.
3.解:∵D是BC的中点,且DE⊥BC,
∴DE是BC的垂直平分线,CD=BD,
∴CE=BE,故本答案正确;
∴∠C=∠7,
∵AD=AB,
∴∠8=∠ABC=∠6+∠7,
∵∠8=∠C+∠4,
∴∠C+∠4=∠6+∠7,
∴∠4=∠6,即∠CAD=∠ABE,故本答案正确;
作AG⊥BD于点G,交BE于点H,
∵AD=AB,DE⊥BC,
∴∠2=∠3,DG=BG=BD,DE∥AG,
∴△CDE∽△CGA,△BGH∽△BDE,EH=BH,∠EDA=∠3,∠5=∠1,
∴CD:CG=DE:AG,HG=DE,
设DG=x,DE=2y,则GB=x,CD=2x,CG=3x,
∴2x:3x=2y:AG,
解得:AG=3y,HG=y,
∴AH=2y,
∴DE=AH,且∠EDA=∠3,∠5=∠1
∴△DEF≌△AHF
∴AF=DF,故本答案正确;
EF=HF=EH,且EH=BH,
∴EF:BF=1:3,
∴S△ABF=3S△AEF,
∵S△DEF=S△AEF,
∴S△ABF=3S△DEF,故本答案正确;
∵∠1=∠2+∠6,且∠4=∠6,∠2=∠3,
∴∠5=∠3+∠4,
∴∠5≠∠4,
∴△DEF∽△DAE,不成立,故本答案错误.
综上所述:正确的答案有4个.
故选:B.
二.填空题
4.解:分两种情况:
①当∠CED=90°时,如图1,
过E作EF⊥CD于F,
∵AD∥BC,AD<BC,
∴AB与CD不平行,
∴当△ADE、△BCE、△CDE两两相似时,
∴∠BEC=∠CDE=∠ADE,
∵∠A=∠B=∠CED=90°,
∴∠BCE=∠DCE,
∴AE=EF,EF=BE,
∴AE=BE=AB=,
②当∠CDE=90°时,如图2,
∵当△ADE、△BCE、△CDE两两相似时,
∴∠CEB=∠CED=∠AED=60°,
∴∠BCE=∠DCE=30°,
∵∠A=∠B=90°,
∴BE=ED=2AE,
∵AB=3,
∴AE=1,
综上,AE的值为或1.
故答案为:或1.
5.解:∵AD∥BC,∠D=90°,
∴∠C=∠D=90°
∵AD=2,BC=12,DC=10.
设PD=x,则PC=10﹣x;
①若PD:PC=AD:BC,则△PAD∽△PBC
∴x:(10﹣x)=2:12,
解得x=,即PD=;
②若PD:BC=AD:PC,则△PAD∽△CBP
∴x:12=2:(10﹣x),解得:x=4或x=6,即PD=4或PD=6.
∴这样的点P存在的个数有3个.
故答案为3.
三.解答题
6.证明:∵∠B=90°,AB=4,BC=2,
∴AC==2,
∵CE=AC,
∴CE=2,
∵CD=5,
∵==,=,
∴=,
∵∠B=90°,∠ACE=90°,
∴∠BAC+∠BCA=90°,∠BCA+∠DCE=90°.
∴∠BAC=∠DCE.
∴△ABC∽△CED.
7.证明:如图所示:
∵∠BAC=90°,AB=AC,
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,
∴∠1+∠2=180°﹣∠B=135°,
∵∠ADE=45°,
∴∠2+∠3=135°,
∴∠1=∠3,
∵∠B=∠C,
∴△ABD∽△DCE.
8.(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BCE=∠BAC,
又∵BD=CE,
∴△ABD≌△BCE;
(2)答:相似;
理由如下:
∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠BAC﹣∠BAD=∠CBA﹣∠CBE,
∴∠EAF=∠EBA,又∵∠AEF=∠BEA,
∴△EAF∽△EBA.
9.(1)证明:∵AD∥BC,
∴∠PAF=∠AEB.
∵∠PFA=∠ABE=90°,
∴△PFA∽△ABE.
(2)若△EFP∽△ABE,则∠PEF=∠EAB.
∴PE∥AB.
∴四边形ABEP为矩形.
∴PA=EB=2,即x=2.
若△PFE∽△ABE,则∠PEF=∠AEB.
∵∠PAF=∠AEB,
∴∠PEF=∠PAF.
∴PE=PA.
∵PF⊥AE,
∴点F为AE的中点.
∵AE=,
∴EF=AE=.
∵,即,
∴PE=5,即x=5.
∴满足条件的x的值为2或5.
10.解:(1)∠BAE与∠CAD相等.
理由:∵==,
∴△ABC∽△AED,
∴∠BAC=∠EAD,
∴∠BAE=∠CAD;
(2)△ABE与△ACD相似.
∵=,
∴=.
在△ABE与△ACD中,
∵=,∠BAE=∠CAD,
∴△ABE∽△ACD.
11.解:(1)∵△ACD和△BCE都是等边三角形,
∴AC=CD,CE=CB,∠ACD=∠BCE=60°
∴∠ACE=∠DCB=120°.
∴△ACE≌△DCB(SAS);
(2)∵△ACE≌△DCB,
∴∠CAE=∠CDB.
∵∠ADC=∠CAD=∠ACD=∠CBE=60°,
∴DC∥BE,
∴∠CDB=∠DBE,
∴∠CAE=∠DBE,
∴∠DAF=∠DBA.
∴△ADF∽△BAD.
12.解:(1)设PF=m,PE=n,连接EF,如图1,
∵AF,BE是△ABC的中线,
∴EF为△ABC的中位线,AE=b,BF=a,
∴EF∥AB,EF=c,
∴△EFP∽△BPA,
∴,即==,
∴PB=2n,PA=2m,
在Rt△AEP中,∵PE2+PA2=AE2,
∴n2+4m2=b2①,
在Rt△BFP中,∵PF2+PB2=BF2,
∴m2+4n2=a2②,
①+②得5(n2+m2)=(a2+b2),
在Rt△EFP中,∵PE2+PF2=EF2,
∴n2+m2=EF2=c2,
∴5 c2=(a2+b2),
∴a2+b2=5c2;
(2)∵四边形ABCD为菱形,
∴BD⊥AC,
∵E,F分别为线段AO,DO的中点,
∴EF∥AD,EF=AD
而AD∥BC,AD=BC,
∴EF∥BC,EF=BC,
∴E点为BM的中点,F为CM的中点,
而CE⊥BF,
∴由(1)的结论得MB2+MC2=5BC2=5×32=45,
∵AG∥BC,
∴△AEG∽△CEB,
∴==,
∴AG=1,
同理可得DH=1,
∴GH=1,
∴GH∥BC,
∴===,
∴MB=3GM,MC=3MH,
∴9MG2+9MH2=45,
∴MG2+MH2=5.
13.解:(1)∵AD=BC,BC=,
∴AD=,DC=1﹣=.
∴AD2==,AC CD=1×=.
∴AD2=AC CD.
(2)∵AD=BC,AD2=AC CD,
∴BC2=AC CD,即.
又∵∠C=∠C,
∴△BCD∽△ACB.
∴,∠DBC=∠A.
∴DB=CB=AD.
∴∠A=∠ABD,∠C=∠BDC.
设∠A=x,则∠ABD=x,∠DBC=x,∠C=2x.
∵∠A+∠ABC+∠C=180°,
∴x+2x+2x=180°.
解得:x=36°.
∴∠ABD=36°.
14.(1)解:∵S1=BD×ED,S矩形BDEF=BD×ED,
∴S1=S矩形BDEF,
∴S2+S3=S矩形BDEF,
∴S1=S2+S3.
(2)答:△BCD∽△CFB∽△DEC.
证明△BCD∽△DEC;
证明:∵∠EDC+∠BDC=90°,∠CBD+∠BDC=90°,
∴∠EDC=∠CBD,
又∵∠BCD=∠DEC=90°,
∴△BCD∽△DEC.
15.(1)证明:∵∠PBE+∠ABQ=90°,∠PBE+∠PEB=90°,
∴∠ABQ=∠PEB.
在△PBE与△QAB中,
∵∠ABQ=∠PEB,∠BPE=∠AQB=90°,
∴△PBE∽△QAB.
(2)解:△PBE和△BAE相似.
∵△PBE∽△QAB,
∴=.
∵BQ=PB,
∴=.
又∵∠EPB=∠EBA=90°,
∴△PBE∽△BAE.
16.证明:∵AD=AC,
∴∠ADC=∠ACD,
∵D为BC中点,且DE⊥BC,
∴EB=EC.
∴∠B=∠DCF.
∴△ABC∽△FCD.
17.证明:(1)∵点E是BC的中点,BC=2AD,
∴EC=BE=BC=AD,
又∵AD∥BC,
∴四边形AECD为平行四边形,
∴AE∥DC,
∴△AOE∽△COF;
(2)连接DE,
∵AD∥BE,AD=BE,
∴四边形ABED是平行四边形,
又∠ABE=90°,
∴四边形ABED是矩形,
∴GE=GA=GB=GD=BD=AE,
∴E、F分别是BC、CD的中点,
∴EF、GE是△CBD的两条中位线,
∴EF=BD=GD,GE=CD=DF,
又GE=GD,
∴EF=GD=GE=DF,
∴四边形EFDG是菱形.
18.解:(1)根据相似三角形的判定得,与△ABD相似的三角形有:△ACB,△ECD,△AFD,△EFB.
(2)存在t值,使△ADF∽△EDB.理由如下:
∵∠F=180°﹣∠FAD﹣∠FDA=90°﹣∠FDA,∠C=180°﹣∠CED﹣∠CDE=90°﹣∠CDE,∠FDA=∠CDE.
∴∠F=∠C.
∵∠ABD=∠C,
∴∠F=∠ABD.
在△ABD与△AFD中,∠F=∠ABD,∠FAD=∠BAD=90°,AD=AD,
∴△ABD≌△AFD.
∵△ADF∽△EDB,
∴△ADB∽△EDB,而相似比==1.
∴△ADB≌△EDB.
∴∠ABD=∠EBD.
∴∠F=∠ABD=∠EBD.
∵∠F+∠ABD+∠EBD=90°,
∴∠F=30°.
∴∠C=30°.
∴∠ABC=60°.
∴=.
∴t=.
19.解:(1)△ABE与△DEF相似,理由如下:
∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∵∠BEF=90°,
∴∠ABE+∠AEB=∠DEF+∠AEB=90°,
∴∠ABE=∠DEF,
∴△ABE∽△DEF;
(2)当点E位于AD中点时,△ABE、△BEF、△DEF这三个三角形都相似,理由如下:
作EG⊥BF于G,
∵△EBF∽△ABE,
∴∠ABE=∠EBF,
∵∠A=90°,
∴EG=EA,
同理可得:ED=EG,
∴AE=ED,
即E是AD的中点
(3)如图2,
当△CBF∽△EBF∽△ABE∽△DEF时,
∠CBF=∠EBF=∠ABE=∠DEF=30°,
∴AE=AB,
由(2)知:AD=2AE=AB,
∴==,
∵==,
∴DF=AE=×AB=AB,
∵CD=AB,
∴DF=CD,
∴=.
20.证明:∵AB=AC,
∴∠B=∠C,
∵∠ADB=∠C+∠CAD=∠BDE+∠ADE,∠BDE=∠CAD,
∴∠ADE=∠C,
∴∠B=∠ADE,
∵∠DAE=∠BAD,
∴△ADE∽△ABD.
21.解:设t秒后,则BP=6﹣t,BQ=2t,
(1)△PBQ是等腰三角形,则BP=BQ即6﹣t=2t,解得t=2;
(2)△PQB的面积为BP BQ=(6﹣t)(2t)=5,即(t﹣1)(t﹣5)=0,解得t=1或5.
(3)①△BPQ∽△BAC,则=,即2t=2(6﹣t),解得t=3.
②△BPQ∽△BCA,则有BP:BC=BQ:AB,∴6﹣t:12=2t:6,解得t=1.2
∴当t=3秒或t=1.2秒时以P、B、Q为顶点的三角形和△ABC相似.
22.解:∵∠A=∠A,
∴当∠ACP=∠B,或∠APC=∠ACB;
或,即AC2=AP AB时,△ACP∽△ABC;
故答案为:∠ACP=∠B(或∠APC=∠ACB),或AC2=AP AB;
(1)王华补充的条件是:∠ACP=∠B(或∠APC=∠ACB);或AC2=AP AB;理由如下:
∵∠A=∠A,
∴当∠ACP=∠B,或∠APC=∠ACB;
或,即AC2=AP AB时,△ACP∽△ABC;
故答案为:∠ACP=∠B(或∠APC=∠ACB),或AC2=AP AB;
(2)延长AB到点D,使BD=BC,连接CD,如图所示:
∵AC2=AB2+AB BC=AB(AB+BC)=AB(AB+BD)=AB AD,
∴,
又∵∠A=∠A,∴△ACB∽△ADC,
∴∠ACB=∠D,
∵BC=BD,
∴∠BCD=∠D,
在△ACD中,∠ACB+∠BCD+∠D+∠A=180°,
∴3∠ACB+30°=180°,
∴∠ACB=50°.
23.解:(1)∵点A(1,3),点B(﹣3,0),点C(1,0),
∴∠ACB=90°,OC=1,AC=3,BC=4,
∴AB==5,
若△BDA与△BAC相似(不包含全等),
则∠BAD=90°,
由射影定理得:AC2=BC CD,
∴CD=,
∴OD=OC+CD=1+=
∴点D的坐标为(,0);
(2)存在,m=或;理由如下:
∵∠PBQ=∠ABD,
∴分两种情况:
①当时,△BPQ∽△BAD,
即,
解得:m=;
②当时,△BPQ∽△ABD,
即,
解得:m=.
综上所述:存在这样的m,使得△BPQ与△BDA相似,m=或.
同步练习题(附答案)
一.选择题
1.如图,在四边形ABCD中,∠BAC=90°,AB=6,AC=8,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.下列结论错误的是( )
A.四边形AECD的周长是20 B.△ABC∽△FEC
C.∠B+∠ACD=90° D.EF的长为
2.如图,在△ABC中,点D、E分别在边AB、AC上,则在下列四个条件中:①∠AED=∠B;②DE∥BC;③;④AD BC=DE AC,能满足△ADE∽△ACB的条件有( )
A.1个 B.2个 C.3个 D.4个
3.如图,在△ABC中,D是BC的中点,DE⊥BC交AC于E,已知AD=AB,连接BE交AD于F,下列结论:①BE=CE;②∠CAD=∠ABE;③AF=DF;④S△ABF=3S△DEF;⑤△DEF∽△DAE,其中正确的有( )个.
A.5 B.4 C.3 D.2
二.填空题
4.如图,在四边形ABCD中,AD∥BC,AD<BC,∠ABC=90°,且AB=3,点E是边AB上的动点,当△ADE,△BCE,△CDE两两相似时,则AE= .
5.如图,AD∥BC,∠D=90°,AD=2,BC=12,DC=10,若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有 个.
三.解答题
6.如图,在△ABC中,∠B=90°,AB=4,BC=2,以AC为边作△ACE,∠ACE=90°,AC=CE,延长BC至点D,使CD=5,连接DE.求证:△ABC∽△CED.
7.在△ABC中,∠BAC=90°,AB=AC,点D是BC边上一点,过点D作∠ADE=45°,DE交AC于点E,求证:△ABD∽△DCE.
8.如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.
(1)试说明△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.
如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F.
(1)求证:△PFA∽△ABE;
(2)当点P在射线AD上运动时,设PA=x,是否存在实数x,使以P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,说明理由.
10.如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且==.
(1)试问:∠BAE与∠CAD相等吗?为什么?
(2)试判断△ABE与△ACD是否相似?并说明理由.
11.如图,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连接AE,BD,设AE交CD于点F.
(1)求证:△ACE≌△DCB;
(2)求证:△ADF∽△BAD.
12.尤秀同学遇到了这样一个问题:如图1所示,已知AF,BE是△ABC的中线,且AF⊥BE,垂足为P,设BC=a,AC=b,AB=c.
求证:a2+b2=5c2
该同学仔细分析后,得到如下解题思路:
先连接EF,利用EF为△ABC的中位线得到△EPF∽△BPA,故,设PF=m,PE=n,用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF中利用勾股定理计算,消去m,n即可得证
(1)请你根据以上解题思路帮尤秀同学写出证明过程.
(2)利用题中的结论,解答下列问题:
在边长为3的菱形ABCD中,O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图2所示,求MG2+MH2的值.
13.如图,在△ABC中,AB=AC=1,BC=,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与AC CD的大小关系;
(2)求∠ABD的度数.
14.如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.
(1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,则S1 S2+S3(用“>”、“=”、“<”填空);
(2)写出如图中的三对相似三角形,并选择其中一对进行证明.
15.如图,先把一矩形ABCD纸片对折,设折痕为MN,再把B点叠在折痕线上,得到△ABE.过B点折纸片使D点叠在直线AD上,得折痕PQ.
(1)求证:△PBE∽△QAB;
(2)你认为△PBE和△BAE相似吗?如果相似,给出证明;若不相似,请说明理由.
16.如图,在△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,交BA于点E,EC与AD相交于点F.
求证:△ABC∽△FCD.
17.已知:在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,E是BC的中点,连接AE、AC.
(1)点F是DC上一点,连接EF,交AC于点O(如图1),求证:△AOE∽△COF;
(2)若点F是DC的中点,连接BD,交AE与点G(如图2),求证:四边形EFDG是菱形.
18.已知:如图,Rt△ABC中,∠BAC=90°,D是AC上一点,∠ABD=∠C,直线EF过点D,与BA的延长线相交于F,且EF⊥BC,垂足为E.
(1)写出图中所有与△ABD相似的三角形;
(2)探索:设,是否存在这样的t值,使得△ADF∽△EDB?说明理由.
19.如图,在矩形ABCD中,点E、F分别在边AD、CD上(F不与C重合),且∠BEF=90°
(1)△ABE与△DEF相似吗?为什么?
(2)当点E位于AD上何处时,△ABE、△BEF、△DEF这三个三角形都相似?
(3)当△ABE、△BEF、△DEF、△CBF这四个三角形都相似时,求及的值.
20.如图,在△ABC中,AB=AC,点D、E分别在BC、AB上,且∠BDE=∠CAD.求证:△ADE∽△ABD.
21.在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,设P、Q两点同时出发,移动时间为t秒.
(1)几秒钟后△PBQ是等腰三角形?
(2)几秒钟后△PQB的面积为5cm2?
(3)几秒钟后,以P、B、Q为顶点的三角形和△ABC相似?
22.王华在学习相似三角形时,在北京市义务教育教科书九年级上册第31页遇到这样一道题,如图1,在△ABC中,P是边AB上的一点,连接CP,要使△ACP∽△ABC,还需要补充的一个条件是 ,或 .
请回答:
(1)王华补充的条件是 ,或 .
(2)请你参考上面的图形和结论,探究,解答下面的问题:
如图2,在△ABC中,∠A=30°,AC2=AB2+AB BC.求∠C的度数.
23.已知:点A(1,3),点B(﹣3,0),点C(1,0)
(1)请在x轴上找一点D,使得△BDA与△BAC相似(不包含全等),并求出点D的坐标;
(2)在(1)的条件下,如果P、Q分别是BA、BD上的动点,连接PQ,设BP=DQ=m,问:是否存在这样的m,使得△BPQ与△BDA相似?如存在,请求出m的值;若不存在,请说明理由.
参考答案
1.解:∵∠BAC=90°,AB=6,AC=8,
∴BC==10,
∵AD∥BC,AE∥DC,
∴四边形AECD是平行四边形,
∵∠BAC=90°,E是BC的中点,
∴AE=CE=BC=5,
∴四边形AECD是菱形,
∴菱形AECD的周长是20,
故A选项正确,不符合题意;
∵四边形AECD是菱形,
∴∠ACB=∠ACD,
∵∠B+∠ACB=90°,
∴∠B+∠ACD=90°,
故C选项正确,不符合题意;
如图,过A作AH⊥BC于点H,
∵S△ABC=BC AH=AB AC,
∴AH==,
∵点E是BC的中点,BC=10,四边形AECD是菱形,
∴CD=CE=5,
∵S AECD=CE AH=CD EF,
∴EF=AH=.
故D选项正确,不符合题意;
在Rt△EFC中,EF=,EC=5,
∴FC==,
在Rt△CAB中,AB=6,AC=8,BC=10,
∵=,=,=,
∴△ABC与△FEC不相似,故B选项错误,符合题意.
故选:B.
2.解:①∠B=∠AED,∠A=∠A,则可判断△ADE∽△ACB,故①符合题意;
②DE∥BC,则△ADE∽△ABC,故②不符合题意,
③,且夹角∠A=∠A,能确定△ADE∽△ACB,故③符合题意;
④由AD BC=DE AC可得=,此时不确定∠ADE=∠ACB,故不能确定△ADE∽△ACB,故④不符合题意,
故选:B.
3.解:∵D是BC的中点,且DE⊥BC,
∴DE是BC的垂直平分线,CD=BD,
∴CE=BE,故本答案正确;
∴∠C=∠7,
∵AD=AB,
∴∠8=∠ABC=∠6+∠7,
∵∠8=∠C+∠4,
∴∠C+∠4=∠6+∠7,
∴∠4=∠6,即∠CAD=∠ABE,故本答案正确;
作AG⊥BD于点G,交BE于点H,
∵AD=AB,DE⊥BC,
∴∠2=∠3,DG=BG=BD,DE∥AG,
∴△CDE∽△CGA,△BGH∽△BDE,EH=BH,∠EDA=∠3,∠5=∠1,
∴CD:CG=DE:AG,HG=DE,
设DG=x,DE=2y,则GB=x,CD=2x,CG=3x,
∴2x:3x=2y:AG,
解得:AG=3y,HG=y,
∴AH=2y,
∴DE=AH,且∠EDA=∠3,∠5=∠1
∴△DEF≌△AHF
∴AF=DF,故本答案正确;
EF=HF=EH,且EH=BH,
∴EF:BF=1:3,
∴S△ABF=3S△AEF,
∵S△DEF=S△AEF,
∴S△ABF=3S△DEF,故本答案正确;
∵∠1=∠2+∠6,且∠4=∠6,∠2=∠3,
∴∠5=∠3+∠4,
∴∠5≠∠4,
∴△DEF∽△DAE,不成立,故本答案错误.
综上所述:正确的答案有4个.
故选:B.
二.填空题
4.解:分两种情况:
①当∠CED=90°时,如图1,
过E作EF⊥CD于F,
∵AD∥BC,AD<BC,
∴AB与CD不平行,
∴当△ADE、△BCE、△CDE两两相似时,
∴∠BEC=∠CDE=∠ADE,
∵∠A=∠B=∠CED=90°,
∴∠BCE=∠DCE,
∴AE=EF,EF=BE,
∴AE=BE=AB=,
②当∠CDE=90°时,如图2,
∵当△ADE、△BCE、△CDE两两相似时,
∴∠CEB=∠CED=∠AED=60°,
∴∠BCE=∠DCE=30°,
∵∠A=∠B=90°,
∴BE=ED=2AE,
∵AB=3,
∴AE=1,
综上,AE的值为或1.
故答案为:或1.
5.解:∵AD∥BC,∠D=90°,
∴∠C=∠D=90°
∵AD=2,BC=12,DC=10.
设PD=x,则PC=10﹣x;
①若PD:PC=AD:BC,则△PAD∽△PBC
∴x:(10﹣x)=2:12,
解得x=,即PD=;
②若PD:BC=AD:PC,则△PAD∽△CBP
∴x:12=2:(10﹣x),解得:x=4或x=6,即PD=4或PD=6.
∴这样的点P存在的个数有3个.
故答案为3.
三.解答题
6.证明:∵∠B=90°,AB=4,BC=2,
∴AC==2,
∵CE=AC,
∴CE=2,
∵CD=5,
∵==,=,
∴=,
∵∠B=90°,∠ACE=90°,
∴∠BAC+∠BCA=90°,∠BCA+∠DCE=90°.
∴∠BAC=∠DCE.
∴△ABC∽△CED.
7.证明:如图所示:
∵∠BAC=90°,AB=AC,
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,
∴∠1+∠2=180°﹣∠B=135°,
∵∠ADE=45°,
∴∠2+∠3=135°,
∴∠1=∠3,
∵∠B=∠C,
∴△ABD∽△DCE.
8.(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BCE=∠BAC,
又∵BD=CE,
∴△ABD≌△BCE;
(2)答:相似;
理由如下:
∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠BAC﹣∠BAD=∠CBA﹣∠CBE,
∴∠EAF=∠EBA,又∵∠AEF=∠BEA,
∴△EAF∽△EBA.
9.(1)证明:∵AD∥BC,
∴∠PAF=∠AEB.
∵∠PFA=∠ABE=90°,
∴△PFA∽△ABE.
(2)若△EFP∽△ABE,则∠PEF=∠EAB.
∴PE∥AB.
∴四边形ABEP为矩形.
∴PA=EB=2,即x=2.
若△PFE∽△ABE,则∠PEF=∠AEB.
∵∠PAF=∠AEB,
∴∠PEF=∠PAF.
∴PE=PA.
∵PF⊥AE,
∴点F为AE的中点.
∵AE=,
∴EF=AE=.
∵,即,
∴PE=5,即x=5.
∴满足条件的x的值为2或5.
10.解:(1)∠BAE与∠CAD相等.
理由:∵==,
∴△ABC∽△AED,
∴∠BAC=∠EAD,
∴∠BAE=∠CAD;
(2)△ABE与△ACD相似.
∵=,
∴=.
在△ABE与△ACD中,
∵=,∠BAE=∠CAD,
∴△ABE∽△ACD.
11.解:(1)∵△ACD和△BCE都是等边三角形,
∴AC=CD,CE=CB,∠ACD=∠BCE=60°
∴∠ACE=∠DCB=120°.
∴△ACE≌△DCB(SAS);
(2)∵△ACE≌△DCB,
∴∠CAE=∠CDB.
∵∠ADC=∠CAD=∠ACD=∠CBE=60°,
∴DC∥BE,
∴∠CDB=∠DBE,
∴∠CAE=∠DBE,
∴∠DAF=∠DBA.
∴△ADF∽△BAD.
12.解:(1)设PF=m,PE=n,连接EF,如图1,
∵AF,BE是△ABC的中线,
∴EF为△ABC的中位线,AE=b,BF=a,
∴EF∥AB,EF=c,
∴△EFP∽△BPA,
∴,即==,
∴PB=2n,PA=2m,
在Rt△AEP中,∵PE2+PA2=AE2,
∴n2+4m2=b2①,
在Rt△BFP中,∵PF2+PB2=BF2,
∴m2+4n2=a2②,
①+②得5(n2+m2)=(a2+b2),
在Rt△EFP中,∵PE2+PF2=EF2,
∴n2+m2=EF2=c2,
∴5 c2=(a2+b2),
∴a2+b2=5c2;
(2)∵四边形ABCD为菱形,
∴BD⊥AC,
∵E,F分别为线段AO,DO的中点,
∴EF∥AD,EF=AD
而AD∥BC,AD=BC,
∴EF∥BC,EF=BC,
∴E点为BM的中点,F为CM的中点,
而CE⊥BF,
∴由(1)的结论得MB2+MC2=5BC2=5×32=45,
∵AG∥BC,
∴△AEG∽△CEB,
∴==,
∴AG=1,
同理可得DH=1,
∴GH=1,
∴GH∥BC,
∴===,
∴MB=3GM,MC=3MH,
∴9MG2+9MH2=45,
∴MG2+MH2=5.
13.解:(1)∵AD=BC,BC=,
∴AD=,DC=1﹣=.
∴AD2==,AC CD=1×=.
∴AD2=AC CD.
(2)∵AD=BC,AD2=AC CD,
∴BC2=AC CD,即.
又∵∠C=∠C,
∴△BCD∽△ACB.
∴,∠DBC=∠A.
∴DB=CB=AD.
∴∠A=∠ABD,∠C=∠BDC.
设∠A=x,则∠ABD=x,∠DBC=x,∠C=2x.
∵∠A+∠ABC+∠C=180°,
∴x+2x+2x=180°.
解得:x=36°.
∴∠ABD=36°.
14.(1)解:∵S1=BD×ED,S矩形BDEF=BD×ED,
∴S1=S矩形BDEF,
∴S2+S3=S矩形BDEF,
∴S1=S2+S3.
(2)答:△BCD∽△CFB∽△DEC.
证明△BCD∽△DEC;
证明:∵∠EDC+∠BDC=90°,∠CBD+∠BDC=90°,
∴∠EDC=∠CBD,
又∵∠BCD=∠DEC=90°,
∴△BCD∽△DEC.
15.(1)证明:∵∠PBE+∠ABQ=90°,∠PBE+∠PEB=90°,
∴∠ABQ=∠PEB.
在△PBE与△QAB中,
∵∠ABQ=∠PEB,∠BPE=∠AQB=90°,
∴△PBE∽△QAB.
(2)解:△PBE和△BAE相似.
∵△PBE∽△QAB,
∴=.
∵BQ=PB,
∴=.
又∵∠EPB=∠EBA=90°,
∴△PBE∽△BAE.
16.证明:∵AD=AC,
∴∠ADC=∠ACD,
∵D为BC中点,且DE⊥BC,
∴EB=EC.
∴∠B=∠DCF.
∴△ABC∽△FCD.
17.证明:(1)∵点E是BC的中点,BC=2AD,
∴EC=BE=BC=AD,
又∵AD∥BC,
∴四边形AECD为平行四边形,
∴AE∥DC,
∴△AOE∽△COF;
(2)连接DE,
∵AD∥BE,AD=BE,
∴四边形ABED是平行四边形,
又∠ABE=90°,
∴四边形ABED是矩形,
∴GE=GA=GB=GD=BD=AE,
∴E、F分别是BC、CD的中点,
∴EF、GE是△CBD的两条中位线,
∴EF=BD=GD,GE=CD=DF,
又GE=GD,
∴EF=GD=GE=DF,
∴四边形EFDG是菱形.
18.解:(1)根据相似三角形的判定得,与△ABD相似的三角形有:△ACB,△ECD,△AFD,△EFB.
(2)存在t值,使△ADF∽△EDB.理由如下:
∵∠F=180°﹣∠FAD﹣∠FDA=90°﹣∠FDA,∠C=180°﹣∠CED﹣∠CDE=90°﹣∠CDE,∠FDA=∠CDE.
∴∠F=∠C.
∵∠ABD=∠C,
∴∠F=∠ABD.
在△ABD与△AFD中,∠F=∠ABD,∠FAD=∠BAD=90°,AD=AD,
∴△ABD≌△AFD.
∵△ADF∽△EDB,
∴△ADB∽△EDB,而相似比==1.
∴△ADB≌△EDB.
∴∠ABD=∠EBD.
∴∠F=∠ABD=∠EBD.
∵∠F+∠ABD+∠EBD=90°,
∴∠F=30°.
∴∠C=30°.
∴∠ABC=60°.
∴=.
∴t=.
19.解:(1)△ABE与△DEF相似,理由如下:
∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∵∠BEF=90°,
∴∠ABE+∠AEB=∠DEF+∠AEB=90°,
∴∠ABE=∠DEF,
∴△ABE∽△DEF;
(2)当点E位于AD中点时,△ABE、△BEF、△DEF这三个三角形都相似,理由如下:
作EG⊥BF于G,
∵△EBF∽△ABE,
∴∠ABE=∠EBF,
∵∠A=90°,
∴EG=EA,
同理可得:ED=EG,
∴AE=ED,
即E是AD的中点
(3)如图2,
当△CBF∽△EBF∽△ABE∽△DEF时,
∠CBF=∠EBF=∠ABE=∠DEF=30°,
∴AE=AB,
由(2)知:AD=2AE=AB,
∴==,
∵==,
∴DF=AE=×AB=AB,
∵CD=AB,
∴DF=CD,
∴=.
20.证明:∵AB=AC,
∴∠B=∠C,
∵∠ADB=∠C+∠CAD=∠BDE+∠ADE,∠BDE=∠CAD,
∴∠ADE=∠C,
∴∠B=∠ADE,
∵∠DAE=∠BAD,
∴△ADE∽△ABD.
21.解:设t秒后,则BP=6﹣t,BQ=2t,
(1)△PBQ是等腰三角形,则BP=BQ即6﹣t=2t,解得t=2;
(2)△PQB的面积为BP BQ=(6﹣t)(2t)=5,即(t﹣1)(t﹣5)=0,解得t=1或5.
(3)①△BPQ∽△BAC,则=,即2t=2(6﹣t),解得t=3.
②△BPQ∽△BCA,则有BP:BC=BQ:AB,∴6﹣t:12=2t:6,解得t=1.2
∴当t=3秒或t=1.2秒时以P、B、Q为顶点的三角形和△ABC相似.
22.解:∵∠A=∠A,
∴当∠ACP=∠B,或∠APC=∠ACB;
或,即AC2=AP AB时,△ACP∽△ABC;
故答案为:∠ACP=∠B(或∠APC=∠ACB),或AC2=AP AB;
(1)王华补充的条件是:∠ACP=∠B(或∠APC=∠ACB);或AC2=AP AB;理由如下:
∵∠A=∠A,
∴当∠ACP=∠B,或∠APC=∠ACB;
或,即AC2=AP AB时,△ACP∽△ABC;
故答案为:∠ACP=∠B(或∠APC=∠ACB),或AC2=AP AB;
(2)延长AB到点D,使BD=BC,连接CD,如图所示:
∵AC2=AB2+AB BC=AB(AB+BC)=AB(AB+BD)=AB AD,
∴,
又∵∠A=∠A,∴△ACB∽△ADC,
∴∠ACB=∠D,
∵BC=BD,
∴∠BCD=∠D,
在△ACD中,∠ACB+∠BCD+∠D+∠A=180°,
∴3∠ACB+30°=180°,
∴∠ACB=50°.
23.解:(1)∵点A(1,3),点B(﹣3,0),点C(1,0),
∴∠ACB=90°,OC=1,AC=3,BC=4,
∴AB==5,
若△BDA与△BAC相似(不包含全等),
则∠BAD=90°,
由射影定理得:AC2=BC CD,
∴CD=,
∴OD=OC+CD=1+=
∴点D的坐标为(,0);
(2)存在,m=或;理由如下:
∵∠PBQ=∠ABD,
∴分两种情况:
①当时,△BPQ∽△BAD,
即,
解得:m=;
②当时,△BPQ∽△ABD,
即,
解得:m=.
综上所述:存在这样的m,使得△BPQ与△BDA相似,m=或.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
