2022-2023学年人教版 八年级数学上册11.2三角形的角 一课一练(word版含答案)
文档属性
| 名称 | 2022-2023学年人教版 八年级数学上册11.2三角形的角 一课一练(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 214.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-12 00:00:00 | ||
图片预览

文档简介
人教版 八年级数学上册 11.2三角形的角
一.选择题
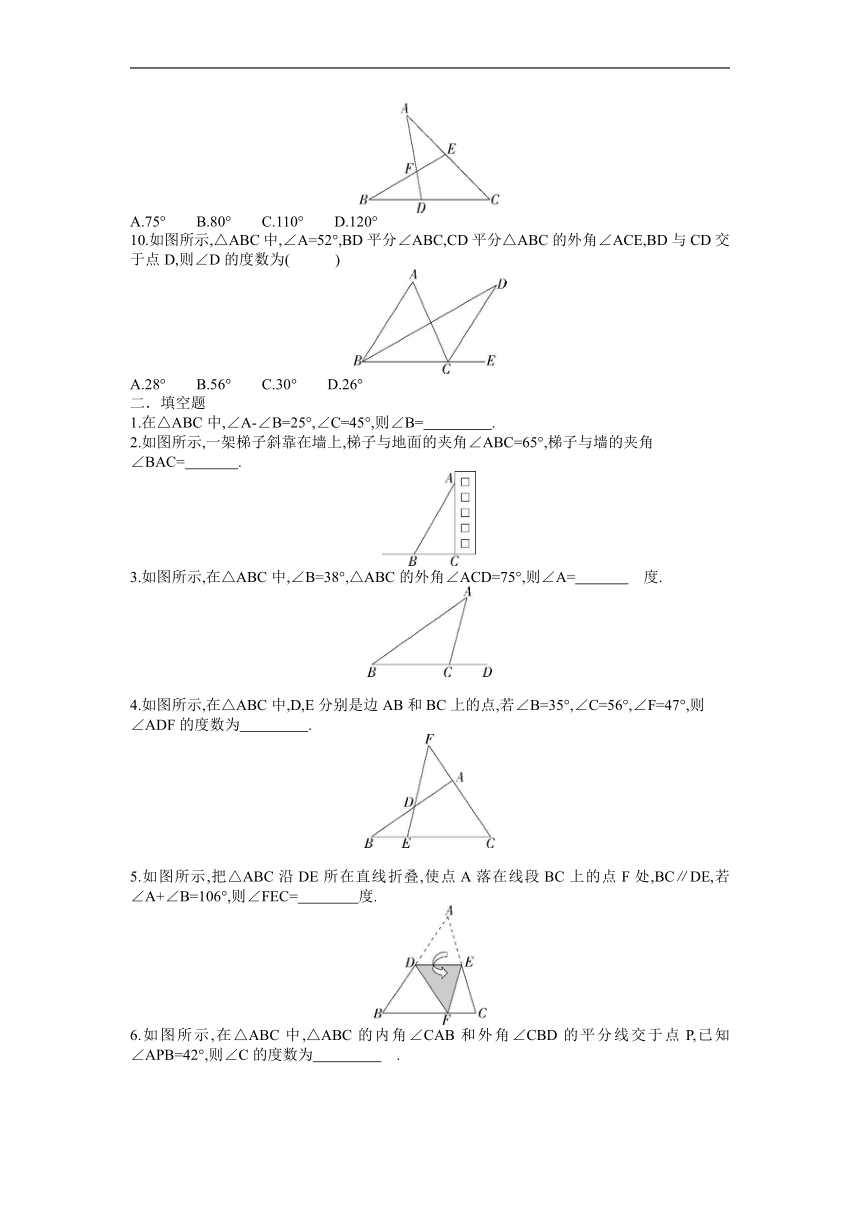
1.如图所示,在△ABC中,∠A=60°,∠B=40°,则∠C的度数为( )
A. 100° B. 80° C. 60° D. 40°
2. 已知△ABC的两个内角∠A=35°,∠B=65°,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
3. 如图所示,在△ABC中,∠A=50°,∠C=80°,点D,E分别在AB和AC上,且DE∥BC.则∠ADE的度数是( )
A.40° B.50° C.60° D.70°
4. 在一个直角三角形中,有一个锐角等于25°,则另一个锐角的度数是( )
A.75° B.65° C.55° D.45°
在△ABC中,满足下列条件:①∠A=60°,∠C=30°;②∠A+∠B=∠C;
③∠A∶∠B∶∠C=3∶4∶5;④∠A=90°-∠C.能确定△ABC是直角三角形的有( )
A. 1个 B. 2个 C. 3个 D. 4个
6.已知直线l1∥l2,将一块直角三角板ABC(其中∠A=30°,∠C=60°)按如图所示的方式放置,若∠1=74°,则∠2等于( )
A.56° B.64° C.66° D.76°
7. 如图所示,在Rt△ABC中,∠ACB=90°,∠A=65°,点D是AB延长线上的一点,则∠CBD的度数是( )
A.125° B.135° C.145° D.155°
8.如图所示,△ABC中,∠ACB=90°,且CD∥AB,∠B=50°,则∠1等于( )
A.30° B.40° C.50° D.60°
9.如图所示,点D、E分别在线段BC、AC上,连接AD、BE交于点F.∠A=35°,∠B=40°,∠C=45°,则∠AFB的大小为( )
A.75° B.80° C.110° D.120°
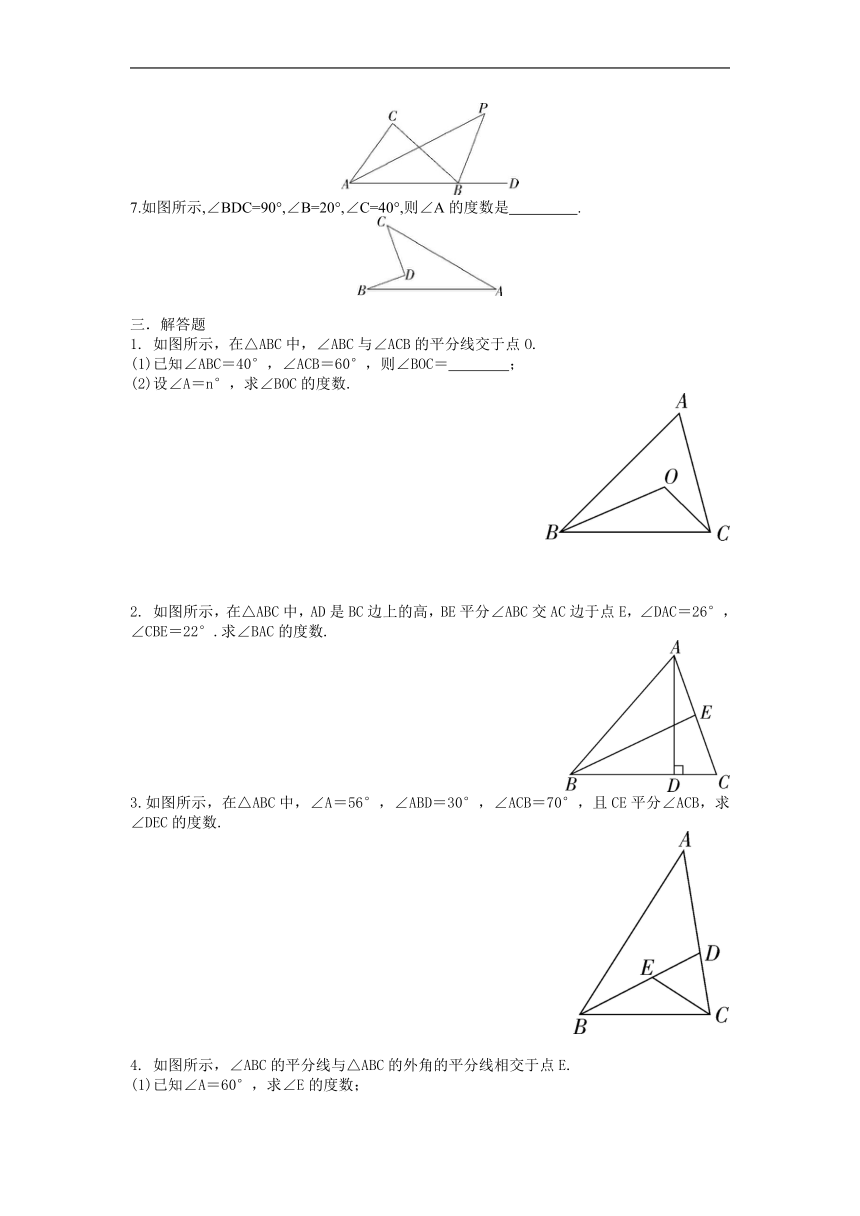
10.如图所示,△ABC中,∠A=52°,BD平分∠ABC,CD平分△ABC的外角∠ACE,BD与CD交于点D,则∠D的度数为( )
A.28° B.56° C.30° D.26°
二.填空题
1.在△ABC中,∠A-∠B=25°,∠C=45°,则∠B= .
2.如图所示,一架梯子斜靠在墙上,梯子与地面的夹角∠ABC=65°,梯子与墙的夹角∠BAC= .
3.如图所示,在△ABC中,∠B=38°,△ABC的外角∠ACD=75°,则∠A= 度.
4.如图所示,在△ABC中,D,E分别是边AB和BC上的点,若∠B=35°,∠C=56°,∠F=47°,则∠ADF的度数为 .
5.如图所示,把△ABC沿DE所在直线折叠,使点A落在线段BC上的点F处,BC∥DE,若∠A+∠B=106°,则∠FEC= 度.
6.如图所示,在△ABC中,△ABC的内角∠CAB和外角∠CBD的平分线交于点P,已知∠APB=42°,则∠C的度数为 .
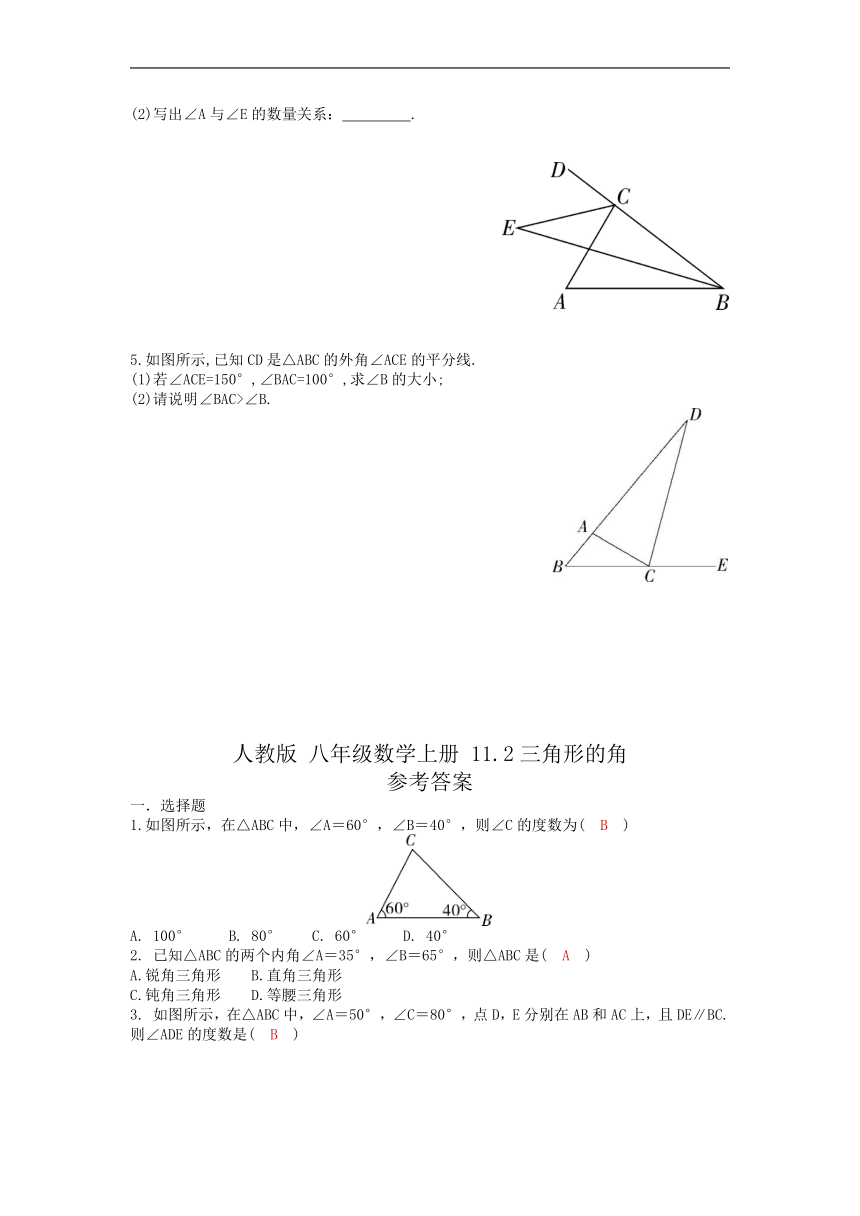
7.如图所示,∠BDC=90°,∠B=20°,∠C=40°,则∠A的度数是 .
三.解答题
1. 如图所示,在△ABC中,∠ABC与∠ACB的平分线交于点O.
(1)已知∠ABC=40°,∠ACB=60°,则∠BOC= ;
(2)设∠A=n°,求∠BOC的度数.
2. 如图所示,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于点E,∠DAC=26°,∠CBE=22°.求∠BAC的度数.
3.如图所示,在△ABC中,∠A=56°,∠ABD=30°,∠ACB=70°,且CE平分∠ACB,求∠DEC的度数.
4. 如图所示,∠ABC的平分线与△ABC的外角的平分线相交于点E.
(1)已知∠A=60°,求∠E的度数;
(2)写出∠A与∠E的数量关系: .
5.如图所示,已知CD是△ABC的外角∠ACE的平分线.
(1)若∠ACE=150°,∠BAC=100°,求∠B的大小;
(2)请说明∠BAC>∠B.
人教版 八年级数学上册 11.2三角形的角
参考答案
一.选择题
1.如图所示,在△ABC中,∠A=60°,∠B=40°,则∠C的度数为( B )
A. 100° B. 80° C. 60° D. 40°
2. 已知△ABC的两个内角∠A=35°,∠B=65°,则△ABC是( A )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
3. 如图所示,在△ABC中,∠A=50°,∠C=80°,点D,E分别在AB和AC上,且DE∥BC.则∠ADE的度数是( B )
A.40° B.50° C.60° D.70°
4. 在一个直角三角形中,有一个锐角等于25°,则另一个锐角的度数是( B )
A.75° B.65° C.55° D.45°
5.在△ABC中,满足下列条件:①∠A=60°,∠C=30°;②∠A+∠B=∠C;
③∠A∶∠B∶∠C=3∶4∶5;④∠A=90°-∠C.能确定△ABC是直角三角形的有( C )
A. 1个 B. 2个 C. 3个 D. 4个
6.已知直线l1∥l2,将一块直角三角板ABC(其中∠A=30°,∠C=60°)按如图所示的方式放置,若∠1=74°,则∠2等于( D )
A.56° B.64° C.66° D.76°
7. 如图所示,在Rt△ABC中,∠ACB=90°,∠A=65°,点D是AB延长线上的一点,则∠CBD的度数是( D )
A.125° B.135° C.145° D.155°
8.如图所示,△ABC中,∠ACB=90°,且CD∥AB,∠B=50°,则∠1等于( B )
A.30° B.40° C.50° D.60°
9.如图所示,点D、E分别在线段BC、AC上,连接AD、BE交于点F.∠A=35°,∠B=40°,∠C=45°,则∠AFB的大小为( D )
A.75° B.80° C.110° D.120°
10.如图所示,△ABC中,∠A=52°,BD平分∠ABC,CD平分△ABC的外角∠ACE,BD与CD交于点D,则∠D的度数为( D )
A.28° B.56° C.30° D.26°
二.填空题
1.在△ABC中,∠A-∠B=25°,∠C=45°,则∠B= 55° .
2.如图所示,一架梯子斜靠在墙上,梯子与地面的夹角∠ABC=65°,梯子与墙的夹角∠BAC= 25° .
3.如图所示,在△ABC中,∠B=38°,△ABC的外角∠ACD=75°,则∠A= 37 度.
4.如图所示,在△ABC中,D,E分别是边AB和BC上的点,若∠B=35°,∠C=56°,∠F=47°,则∠ADF的度数为 42° .
5.如图所示,把△ABC沿DE所在直线折叠,使点A落在线段BC上的点F处,BC∥DE,若∠A+∠B=106°,则∠FEC= 32 度.
6.如图所示,在△ABC中,△ABC的内角∠CAB和外角∠CBD的平分线交于点P,已知∠APB=42°,则∠C的度数为 84° .
7.如图所示,∠BDC=90°,∠B=20°,∠C=40°,则∠A的度数是 30° .
三.解答题
1. 如图所示,在△ABC中,∠ABC与∠ACB的平分线交于点O.
(1)已知∠ABC=40°,∠ACB=60°,则∠BOC= 130° ;
(2)设∠A=n°,求∠BOC的度数.
解:∵∠A=n°,
∴∠ABC+∠ACB=180°-n°.
又∵∠OBC=∠ABC,
∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=90°-n°.
∴∠BOC=180°-(∠OBC+∠OCB)=90°+n°.
2. 如图所示,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于点E,∠DAC=26°,∠CBE=22°.求∠BAC的度数.
解:∵AD是BC边上的高,
∴∠ADC=90°.
∵∠DAC=26°,
∴∠C=90°-26°=64°.
∵BE平分∠ABC,∠CBE=22°,
∴∠ABC=2∠CBE=2×22°=44°.
∴∠BAC=180°-∠ABC-∠C=72°.
3.如图所示,在△ABC中,∠A=56°,∠ABD=30°,∠ACB=70°,且CE平分∠ACB,求∠DEC的度数.
解:在△ABC中,
∵∠A=56°,∠ACB=70°,
∴∠ABC=54°.
∵∠ABD=30°,
∴∠CBD=∠ABC-∠ABD=24°.∵CE平分∠ACB,
∴∠BCE=∠ACB=35°.
∴在△BCE中,∠DEC=∠CBD+∠BCE=59°.
4. 如图所示,∠ABC的平分线与△ABC的外角的平分线相交于点E.
(1)已知∠A=60°,求∠E的度数;
(2)写出∠A与∠E的数量关系: ∠A=2∠E .
解:(1)∵CE,BE分别平分∠ACD,∠ABC,
∴∠ECD=∠ACD,
∠EBC=∠ABC.
∴∠E=∠ECD-∠EBD=(∠ACD-∠ABC)=∠A=30°.
5.如图所示,已知CD是△ABC的外角∠ACE的平分线.
(1)若∠ACE=150°,∠BAC=100°,求∠B的大小;
(2)请说明∠BAC>∠B.
解: (1)∵∠ACE=150°,∠BAC=100°,
∴∠B=∠ACE-∠BAC=150°-100°=50°.
(2)证明:∵CD是△ABC的外角∠ACE的平分线,∴∠ACD=∠ECD,
∵∠BAC是△ACD的外角,
∴∠BAC>∠ACD,∴∠BAC>∠ECD,
∵∠ECD是△BCD的外角,∴∠ECD>∠B,∴∠BAC>∠B.
一.选择题
1.如图所示,在△ABC中,∠A=60°,∠B=40°,则∠C的度数为( )
A. 100° B. 80° C. 60° D. 40°
2. 已知△ABC的两个内角∠A=35°,∠B=65°,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
3. 如图所示,在△ABC中,∠A=50°,∠C=80°,点D,E分别在AB和AC上,且DE∥BC.则∠ADE的度数是( )
A.40° B.50° C.60° D.70°
4. 在一个直角三角形中,有一个锐角等于25°,则另一个锐角的度数是( )
A.75° B.65° C.55° D.45°
在△ABC中,满足下列条件:①∠A=60°,∠C=30°;②∠A+∠B=∠C;
③∠A∶∠B∶∠C=3∶4∶5;④∠A=90°-∠C.能确定△ABC是直角三角形的有( )
A. 1个 B. 2个 C. 3个 D. 4个
6.已知直线l1∥l2,将一块直角三角板ABC(其中∠A=30°,∠C=60°)按如图所示的方式放置,若∠1=74°,则∠2等于( )
A.56° B.64° C.66° D.76°
7. 如图所示,在Rt△ABC中,∠ACB=90°,∠A=65°,点D是AB延长线上的一点,则∠CBD的度数是( )
A.125° B.135° C.145° D.155°
8.如图所示,△ABC中,∠ACB=90°,且CD∥AB,∠B=50°,则∠1等于( )
A.30° B.40° C.50° D.60°
9.如图所示,点D、E分别在线段BC、AC上,连接AD、BE交于点F.∠A=35°,∠B=40°,∠C=45°,则∠AFB的大小为( )
A.75° B.80° C.110° D.120°
10.如图所示,△ABC中,∠A=52°,BD平分∠ABC,CD平分△ABC的外角∠ACE,BD与CD交于点D,则∠D的度数为( )
A.28° B.56° C.30° D.26°
二.填空题
1.在△ABC中,∠A-∠B=25°,∠C=45°,则∠B= .
2.如图所示,一架梯子斜靠在墙上,梯子与地面的夹角∠ABC=65°,梯子与墙的夹角∠BAC= .
3.如图所示,在△ABC中,∠B=38°,△ABC的外角∠ACD=75°,则∠A= 度.
4.如图所示,在△ABC中,D,E分别是边AB和BC上的点,若∠B=35°,∠C=56°,∠F=47°,则∠ADF的度数为 .
5.如图所示,把△ABC沿DE所在直线折叠,使点A落在线段BC上的点F处,BC∥DE,若∠A+∠B=106°,则∠FEC= 度.
6.如图所示,在△ABC中,△ABC的内角∠CAB和外角∠CBD的平分线交于点P,已知∠APB=42°,则∠C的度数为 .
7.如图所示,∠BDC=90°,∠B=20°,∠C=40°,则∠A的度数是 .
三.解答题
1. 如图所示,在△ABC中,∠ABC与∠ACB的平分线交于点O.
(1)已知∠ABC=40°,∠ACB=60°,则∠BOC= ;
(2)设∠A=n°,求∠BOC的度数.
2. 如图所示,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于点E,∠DAC=26°,∠CBE=22°.求∠BAC的度数.
3.如图所示,在△ABC中,∠A=56°,∠ABD=30°,∠ACB=70°,且CE平分∠ACB,求∠DEC的度数.
4. 如图所示,∠ABC的平分线与△ABC的外角的平分线相交于点E.
(1)已知∠A=60°,求∠E的度数;
(2)写出∠A与∠E的数量关系: .
5.如图所示,已知CD是△ABC的外角∠ACE的平分线.
(1)若∠ACE=150°,∠BAC=100°,求∠B的大小;
(2)请说明∠BAC>∠B.
人教版 八年级数学上册 11.2三角形的角
参考答案
一.选择题
1.如图所示,在△ABC中,∠A=60°,∠B=40°,则∠C的度数为( B )
A. 100° B. 80° C. 60° D. 40°
2. 已知△ABC的两个内角∠A=35°,∠B=65°,则△ABC是( A )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
3. 如图所示,在△ABC中,∠A=50°,∠C=80°,点D,E分别在AB和AC上,且DE∥BC.则∠ADE的度数是( B )
A.40° B.50° C.60° D.70°
4. 在一个直角三角形中,有一个锐角等于25°,则另一个锐角的度数是( B )
A.75° B.65° C.55° D.45°
5.在△ABC中,满足下列条件:①∠A=60°,∠C=30°;②∠A+∠B=∠C;
③∠A∶∠B∶∠C=3∶4∶5;④∠A=90°-∠C.能确定△ABC是直角三角形的有( C )
A. 1个 B. 2个 C. 3个 D. 4个
6.已知直线l1∥l2,将一块直角三角板ABC(其中∠A=30°,∠C=60°)按如图所示的方式放置,若∠1=74°,则∠2等于( D )
A.56° B.64° C.66° D.76°
7. 如图所示,在Rt△ABC中,∠ACB=90°,∠A=65°,点D是AB延长线上的一点,则∠CBD的度数是( D )
A.125° B.135° C.145° D.155°
8.如图所示,△ABC中,∠ACB=90°,且CD∥AB,∠B=50°,则∠1等于( B )
A.30° B.40° C.50° D.60°
9.如图所示,点D、E分别在线段BC、AC上,连接AD、BE交于点F.∠A=35°,∠B=40°,∠C=45°,则∠AFB的大小为( D )
A.75° B.80° C.110° D.120°
10.如图所示,△ABC中,∠A=52°,BD平分∠ABC,CD平分△ABC的外角∠ACE,BD与CD交于点D,则∠D的度数为( D )
A.28° B.56° C.30° D.26°
二.填空题
1.在△ABC中,∠A-∠B=25°,∠C=45°,则∠B= 55° .
2.如图所示,一架梯子斜靠在墙上,梯子与地面的夹角∠ABC=65°,梯子与墙的夹角∠BAC= 25° .
3.如图所示,在△ABC中,∠B=38°,△ABC的外角∠ACD=75°,则∠A= 37 度.
4.如图所示,在△ABC中,D,E分别是边AB和BC上的点,若∠B=35°,∠C=56°,∠F=47°,则∠ADF的度数为 42° .
5.如图所示,把△ABC沿DE所在直线折叠,使点A落在线段BC上的点F处,BC∥DE,若∠A+∠B=106°,则∠FEC= 32 度.
6.如图所示,在△ABC中,△ABC的内角∠CAB和外角∠CBD的平分线交于点P,已知∠APB=42°,则∠C的度数为 84° .
7.如图所示,∠BDC=90°,∠B=20°,∠C=40°,则∠A的度数是 30° .
三.解答题
1. 如图所示,在△ABC中,∠ABC与∠ACB的平分线交于点O.
(1)已知∠ABC=40°,∠ACB=60°,则∠BOC= 130° ;
(2)设∠A=n°,求∠BOC的度数.
解:∵∠A=n°,
∴∠ABC+∠ACB=180°-n°.
又∵∠OBC=∠ABC,
∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=90°-n°.
∴∠BOC=180°-(∠OBC+∠OCB)=90°+n°.
2. 如图所示,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于点E,∠DAC=26°,∠CBE=22°.求∠BAC的度数.
解:∵AD是BC边上的高,
∴∠ADC=90°.
∵∠DAC=26°,
∴∠C=90°-26°=64°.
∵BE平分∠ABC,∠CBE=22°,
∴∠ABC=2∠CBE=2×22°=44°.
∴∠BAC=180°-∠ABC-∠C=72°.
3.如图所示,在△ABC中,∠A=56°,∠ABD=30°,∠ACB=70°,且CE平分∠ACB,求∠DEC的度数.
解:在△ABC中,
∵∠A=56°,∠ACB=70°,
∴∠ABC=54°.
∵∠ABD=30°,
∴∠CBD=∠ABC-∠ABD=24°.∵CE平分∠ACB,
∴∠BCE=∠ACB=35°.
∴在△BCE中,∠DEC=∠CBD+∠BCE=59°.
4. 如图所示,∠ABC的平分线与△ABC的外角的平分线相交于点E.
(1)已知∠A=60°,求∠E的度数;
(2)写出∠A与∠E的数量关系: ∠A=2∠E .
解:(1)∵CE,BE分别平分∠ACD,∠ABC,
∴∠ECD=∠ACD,
∠EBC=∠ABC.
∴∠E=∠ECD-∠EBD=(∠ACD-∠ABC)=∠A=30°.
5.如图所示,已知CD是△ABC的外角∠ACE的平分线.
(1)若∠ACE=150°,∠BAC=100°,求∠B的大小;
(2)请说明∠BAC>∠B.
解: (1)∵∠ACE=150°,∠BAC=100°,
∴∠B=∠ACE-∠BAC=150°-100°=50°.
(2)证明:∵CD是△ABC的外角∠ACE的平分线,∴∠ACD=∠ECD,
∵∠BAC是△ACD的外角,
∴∠BAC>∠ACD,∴∠BAC>∠ECD,
∵∠ECD是△BCD的外角,∴∠ECD>∠B,∴∠BAC>∠B.
