2022--2023学年人教版九年级数学上册24.1《圆的有关性质》课时练习(word版含答案)
文档属性
| 名称 | 2022--2023学年人教版九年级数学上册24.1《圆的有关性质》课时练习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-12 00:00:00 | ||
图片预览

文档简介
24.1圆的有关性质
一、单选题
1.如图,已知A,B,C,D四点都在⊙O上,则⊙O中的弦的条数为( )
A.2 B.3 C.4 D.5
2.如图,在平面直角坐标系中,AB是⊙M的直径,若,,则点B的坐标是( )
A. B. C. D.
3.如图所示,,,以点A为圆心,AB长为半径画弧交x轴负半轴于点C,则点C的坐标为( )
A. B. C. D.
4.如图,已知AB为⊙O的弦,,垂足为C,若,,则弦心距OC的长为( ).
A.12 B.10 C.6 D.8
5.如图,为的直径,为的弦,为优弧的中点,,垂足为,,,则的半径为( )
A. B. C. D.
6.如图,是的直径,垂直于弦于点,的延长线交于点.若,,则的长是( )
A.1 B. C.2 D.4
7.如图,A,B是⊙O上的点,∠AOB=120°,C是的中点,若⊙O的半径为5,则四边形ACBO的面积为( )
A.25 B.25 C. D.
8.如图,AB,CD是的弦,延长AB,CD相交于点P.已知,,则的度数是( )
A.30° B.25° C.20° D.10°
9.如图,⊙O在△ABC三边上截得的弦长相等,即DE=FG=MN,∠A=50°,则∠BOC=( )
A.100° B.110° C.115° D.120°
10.如图,点是⊙O的圆心,点、、在⊙O上,,则的度数是( )
A. B. C. D.
二、填空题
11.如图,AB是⊙O的直径,弦CD⊥AB于点E,AB=4,CD=2,则BE的长度是________
12.如图所示,小区内有个圆形花坛O,点C在弦AB上,AC=11,BC=21,OC=13,则这个花坛的面积为_____.(结果保留)
13.如图,四边形ABCD是半圆O的内接四边形,其中AB是直径,点C是弧DB的中点,若∠C=110°,则∠ABC的度数=______.
14.如图,在扇形BOC中,,OD平分交弧BC于点D.点E为半径OB上一动点,若,则长的最小值为______.
15.如图,为的直径,C,D两点在上,,则的度数为______°.
三、解答题
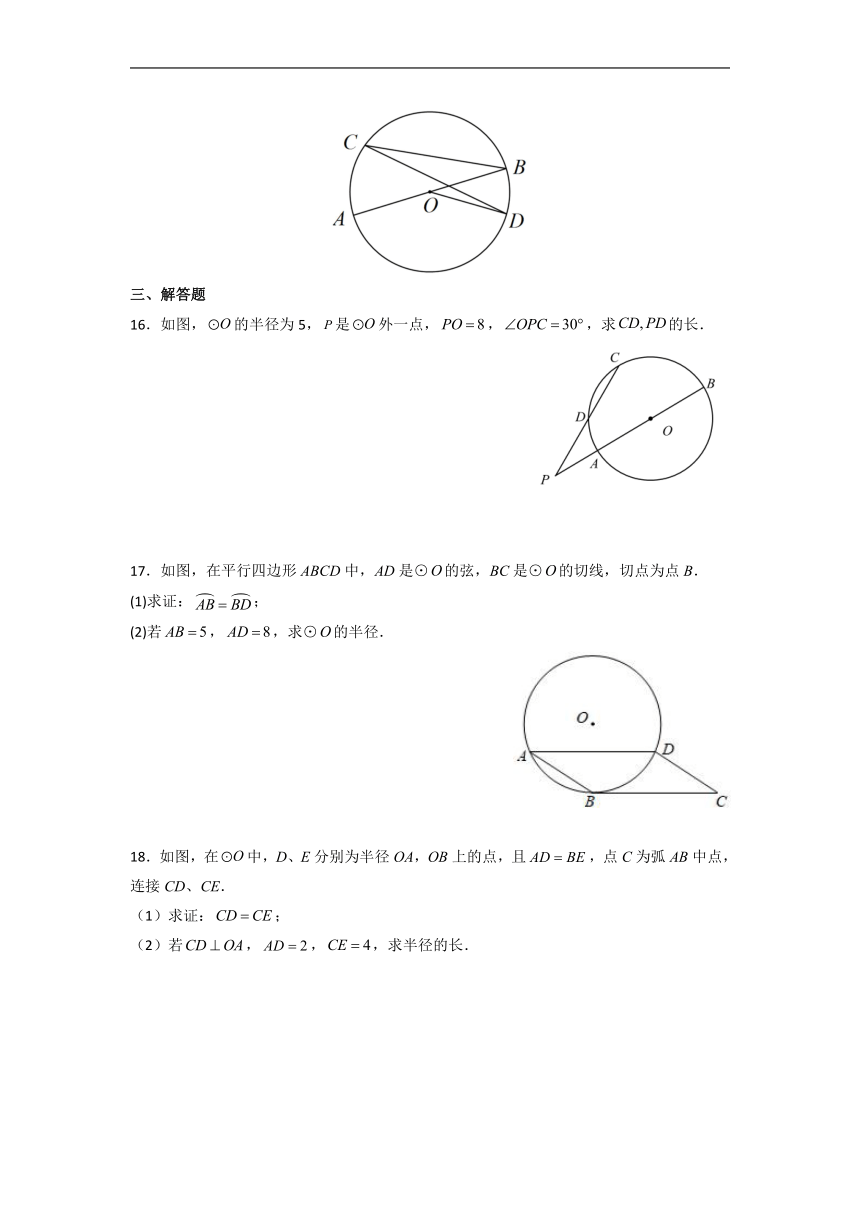
16.如图,的半径为5,是外一点,,,求的长.
17.如图,在平行四边形ABCD中,AD是⊙的弦,BC是⊙的切线,切点为点B.
(1)求证:;
(2)若,,求⊙的半径.
18.如图,在中,D、E分别为半径OA,OB上的点,且,点C为弧AB中点,连接CD、CE.
(1)求证:;
(2)若,,,求半径的长.
19.如图,四边形ABCD中,∠B=∠D,AB=CD,AB与DC不平行,过点A作,交△ABC的外接圆⊙O于点E,连接CE、OA.
(1)求证:四边形ADCE为平行四边形;
(2)求证:AO平分∠BAE.
20.已知的直径,弦与弦交于点E.且,垂足为点F.
(1)如图1,如果,求弦的长;
(2)如图2,如果E为弦的中点,求
21.如图,在⊙O中,点A,B,C在⊙O上,请用无刻度直尺完成下列作图.
(1)如图1,以点C或点B为顶点作一锐角,使该锐角与∠CAB互余(并标记).
(2)如图2,已知交⊙O于点D,过点A作AE将∠BAC平分.
22.如图1,在圆O中,AB=AC,∠ACB=75°,点E在劣弧AC上运动,连接EC、BE,交AC于点F.
(1)求∠E的度数;
(2)当点E运动到使BE⊥AC时,如图2,连接AO并延长,交BE于点G,交BC于点D,交圆O于点M,求证:D为GM中点.
参考答案
一、单选题:1—10 BACCB CDCCB
二、填空题:
11. 13.400π 13.55° 14. 15.150
三、解答题:
16.解:过点O作OE⊥PC,垂足为E,
∴CE=DE,
∵∠P=30°,PO=8,半径为5,
∴OE=4,OA=OD=5,PA=3,
∴PE==,DE==3,
∴CD=2DE=6,PD=PE-DE=.
17.(1)证明:连接,交于点.
是的切线,切点为,
,
,
四边形是平行四边形,
,
,
,
;
(2)解:,过圆心
,
在中,,
,
设的半径为,则,
连接,
在中,,
即,
,
的半径为.
18.解:(1)如图,连接,
,
,即,
点为弧中点,
,
,
在和中,,
,
;
(2)设半径的长为,则,
,
,
由(1)已证:,
,
,
在中,,即,
解得,
故半径的长为5.
19.证明:(1)由圆周角定理得,∠B=∠E,又∠B=∠D,
∴∠E=∠D,
∵,
∴
∴∠E+∠DAE=180°,
∴,
∴四边形AECD为平行四边形;
(2)作OM⊥BA于M,ON⊥AE于N,
∵四边形AECD为平行四边形,
∴AE=CD,
又AB=DC,
∴AE=AB,
又OM⊥BA,ON⊥AE,
而
∴OM=ON,
∴AO平分∠BAE.
20.如图 ,连接OC,
又,
即,
,
则;
如图2,连接,
为直径,
,
,
,
又
是的中位线,
设,
则
解得:,
则
21.(1)连接CO(或BO)并延长,交⊙O于点P(或Q),连接BP(或CQ),CP(或BQ),则∠BCP(或∠CBQ)与∠CAB互余.
标记如图.
(2)如图,连接CD交AB于点F.连接FO,并延长交⊙O于点E,连接AE即可.
22.(1)解:∵AB=AC,∠ACB=75°,
∴∠ABC=∠ACB=75°,
∴∠A=180°-∠ABC-∠ACB=30°,
∵∠E=∠A,
∴∠E=30°;
(2)证明:如图,连接CM,CE,
∵AM是圆O的直径,
∴∠ACM=90°,
∵BE⊥AC,
∴∠AFB=∠ACM=90°,
∴CM∥BE,
∴∠DBG=∠DCM,∠BGD=∠CMD,
∵∠ACB=75°,
∴∠CBF=15°,
∴∠DCM=15°,
∴∠BAM=∠DCM=15°,
∵∠BAC=30°,
∴∠CAM=15°,
∴∠CAM=∠BAM,
∴ ,
∴BD=CD,
在△BDG和△CDM中,
∵∠DBG=∠DCM,∠BGD=∠CMD,BD=CD,
∴△BDG≌△CDM,
∴DG=DM,即D为GM中点.
一、单选题
1.如图,已知A,B,C,D四点都在⊙O上,则⊙O中的弦的条数为( )
A.2 B.3 C.4 D.5
2.如图,在平面直角坐标系中,AB是⊙M的直径,若,,则点B的坐标是( )
A. B. C. D.
3.如图所示,,,以点A为圆心,AB长为半径画弧交x轴负半轴于点C,则点C的坐标为( )
A. B. C. D.
4.如图,已知AB为⊙O的弦,,垂足为C,若,,则弦心距OC的长为( ).
A.12 B.10 C.6 D.8
5.如图,为的直径,为的弦,为优弧的中点,,垂足为,,,则的半径为( )
A. B. C. D.
6.如图,是的直径,垂直于弦于点,的延长线交于点.若,,则的长是( )
A.1 B. C.2 D.4
7.如图,A,B是⊙O上的点,∠AOB=120°,C是的中点,若⊙O的半径为5,则四边形ACBO的面积为( )
A.25 B.25 C. D.
8.如图,AB,CD是的弦,延长AB,CD相交于点P.已知,,则的度数是( )
A.30° B.25° C.20° D.10°
9.如图,⊙O在△ABC三边上截得的弦长相等,即DE=FG=MN,∠A=50°,则∠BOC=( )
A.100° B.110° C.115° D.120°
10.如图,点是⊙O的圆心,点、、在⊙O上,,则的度数是( )
A. B. C. D.
二、填空题
11.如图,AB是⊙O的直径,弦CD⊥AB于点E,AB=4,CD=2,则BE的长度是________
12.如图所示,小区内有个圆形花坛O,点C在弦AB上,AC=11,BC=21,OC=13,则这个花坛的面积为_____.(结果保留)
13.如图,四边形ABCD是半圆O的内接四边形,其中AB是直径,点C是弧DB的中点,若∠C=110°,则∠ABC的度数=______.
14.如图,在扇形BOC中,,OD平分交弧BC于点D.点E为半径OB上一动点,若,则长的最小值为______.
15.如图,为的直径,C,D两点在上,,则的度数为______°.
三、解答题
16.如图,的半径为5,是外一点,,,求的长.
17.如图,在平行四边形ABCD中,AD是⊙的弦,BC是⊙的切线,切点为点B.
(1)求证:;
(2)若,,求⊙的半径.
18.如图,在中,D、E分别为半径OA,OB上的点,且,点C为弧AB中点,连接CD、CE.
(1)求证:;
(2)若,,,求半径的长.
19.如图,四边形ABCD中,∠B=∠D,AB=CD,AB与DC不平行,过点A作,交△ABC的外接圆⊙O于点E,连接CE、OA.
(1)求证:四边形ADCE为平行四边形;
(2)求证:AO平分∠BAE.
20.已知的直径,弦与弦交于点E.且,垂足为点F.
(1)如图1,如果,求弦的长;
(2)如图2,如果E为弦的中点,求
21.如图,在⊙O中,点A,B,C在⊙O上,请用无刻度直尺完成下列作图.
(1)如图1,以点C或点B为顶点作一锐角,使该锐角与∠CAB互余(并标记).
(2)如图2,已知交⊙O于点D,过点A作AE将∠BAC平分.
22.如图1,在圆O中,AB=AC,∠ACB=75°,点E在劣弧AC上运动,连接EC、BE,交AC于点F.
(1)求∠E的度数;
(2)当点E运动到使BE⊥AC时,如图2,连接AO并延长,交BE于点G,交BC于点D,交圆O于点M,求证:D为GM中点.
参考答案
一、单选题:1—10 BACCB CDCCB
二、填空题:
11. 13.400π 13.55° 14. 15.150
三、解答题:
16.解:过点O作OE⊥PC,垂足为E,
∴CE=DE,
∵∠P=30°,PO=8,半径为5,
∴OE=4,OA=OD=5,PA=3,
∴PE==,DE==3,
∴CD=2DE=6,PD=PE-DE=.
17.(1)证明:连接,交于点.
是的切线,切点为,
,
,
四边形是平行四边形,
,
,
,
;
(2)解:,过圆心
,
在中,,
,
设的半径为,则,
连接,
在中,,
即,
,
的半径为.
18.解:(1)如图,连接,
,
,即,
点为弧中点,
,
,
在和中,,
,
;
(2)设半径的长为,则,
,
,
由(1)已证:,
,
,
在中,,即,
解得,
故半径的长为5.
19.证明:(1)由圆周角定理得,∠B=∠E,又∠B=∠D,
∴∠E=∠D,
∵,
∴
∴∠E+∠DAE=180°,
∴,
∴四边形AECD为平行四边形;
(2)作OM⊥BA于M,ON⊥AE于N,
∵四边形AECD为平行四边形,
∴AE=CD,
又AB=DC,
∴AE=AB,
又OM⊥BA,ON⊥AE,
而
∴OM=ON,
∴AO平分∠BAE.
20.如图 ,连接OC,
又,
即,
,
则;
如图2,连接,
为直径,
,
,
,
又
是的中位线,
设,
则
解得:,
则
21.(1)连接CO(或BO)并延长,交⊙O于点P(或Q),连接BP(或CQ),CP(或BQ),则∠BCP(或∠CBQ)与∠CAB互余.
标记如图.
(2)如图,连接CD交AB于点F.连接FO,并延长交⊙O于点E,连接AE即可.
22.(1)解:∵AB=AC,∠ACB=75°,
∴∠ABC=∠ACB=75°,
∴∠A=180°-∠ABC-∠ACB=30°,
∵∠E=∠A,
∴∠E=30°;
(2)证明:如图,连接CM,CE,
∵AM是圆O的直径,
∴∠ACM=90°,
∵BE⊥AC,
∴∠AFB=∠ACM=90°,
∴CM∥BE,
∴∠DBG=∠DCM,∠BGD=∠CMD,
∵∠ACB=75°,
∴∠CBF=15°,
∴∠DCM=15°,
∴∠BAM=∠DCM=15°,
∵∠BAC=30°,
∴∠CAM=15°,
∴∠CAM=∠BAM,
∴ ,
∴BD=CD,
在△BDG和△CDM中,
∵∠DBG=∠DCM,∠BGD=∠CMD,BD=CD,
∴△BDG≌△CDM,
∴DG=DM,即D为GM中点.
同课章节目录
