人教版七年级上册3.4实际问题与一元一次方程之球赛积分课件(共24张PPT)
文档属性
| 名称 | 人教版七年级上册3.4实际问题与一元一次方程之球赛积分课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 250.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-13 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
3.4 实际问题与一元一次方程
————球赛积分与电话费
复习 1.某家具厂生产一种方桌,1立方米的木材可做50个桌面或300条桌腿,现有10立方米的木材,怎样分配生产桌面和桌腿使用的木材,才能使桌面、桌腿刚好配套,共可生产多少张方桌?(一张方桌有1个桌面,4条桌腿)
解:设用x立方米的木材做桌面,则用(10-x)立方米的木材做桌腿.
根据题意,得4×50x=300(10-x),
解得 x=6,所以10-x=4,
可做方桌为50×6=300(张).
答:用6立方米的木材做桌面,4立方米的木材做桌腿,可做300张方桌.
学习目标
1.会阅读、理解表格,并从表格中提取关键信息.(重点)
2.掌握解决“球赛积分表问题”的一般思路,并会根据方程的解的情况对实际问题作出判断.(难点)
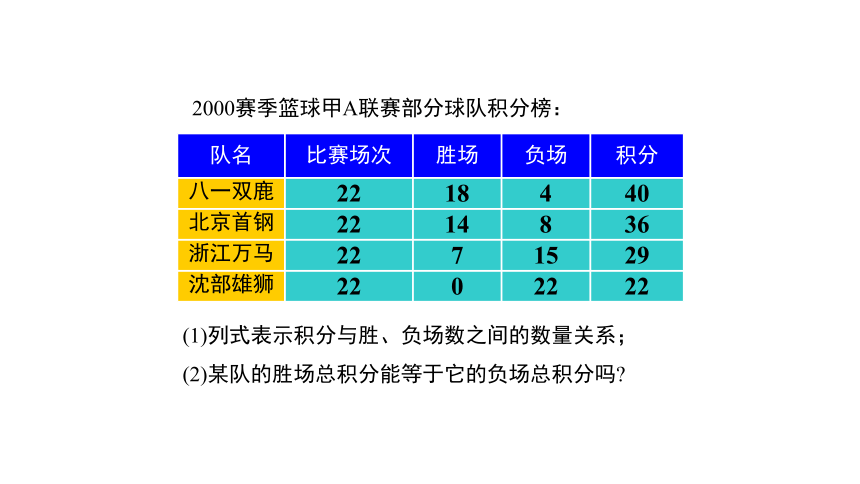
2000赛季篮球甲A联赛部分球队积分榜:
(1)列式表示积分与胜、负场数之间的数量关系;
(2)某队的胜场总积分能等于它的负场总积分吗
队名 比赛场次 胜场 负场 积分
八一双鹿 22 18 4 40
北京首钢 22 14 8 36
浙江万马 22 7 15 29
沈部雄狮 22 0 22 22
解:观察积分榜,从最下面一行可知负一场积1分.
设胜一场积x分,从表中其他任何一行可以列方程,求出x的值.例如,从第一行得出方程:
18x+1×4=40.
由此得出 x=2.
得出负一场积1分,胜一场积2分.
(1)如果一个队胜m场,则负(22-m)场,胜场积分为2m,负场积分为22-m,总积分为
2m+(22-m)=m+22.
(2)设一个队胜了x场,则负了(22-x)场,如果这个队的胜场总积分等于负场总积分,则有方程
2x=22-x
其中,x (胜场)的值必须是整数,所以 不符合实际.由此可以判定没有哪个队伍的胜场总积分等于负场总积分.
当堂练习
1.某球队参加比赛,开局9场保持不败,积21分,比赛规则:胜一场得3分,平一场得1分,则该队共胜( )
A.4场 B.5场 C.6场 D.7场
2.中国男篮CBA职业联赛的积分办法是:胜一场积2分,负一场积1分,某支球队参加了12场比赛,总积分恰是所胜场数的4倍,则该球队共胜____场.
C
4
学习目标
1.掌握解决“电话计费问题”的一般思路.(难点)
2.体验建立方程模型解决问题的一般过程.(重点)
导入新课
情境引入
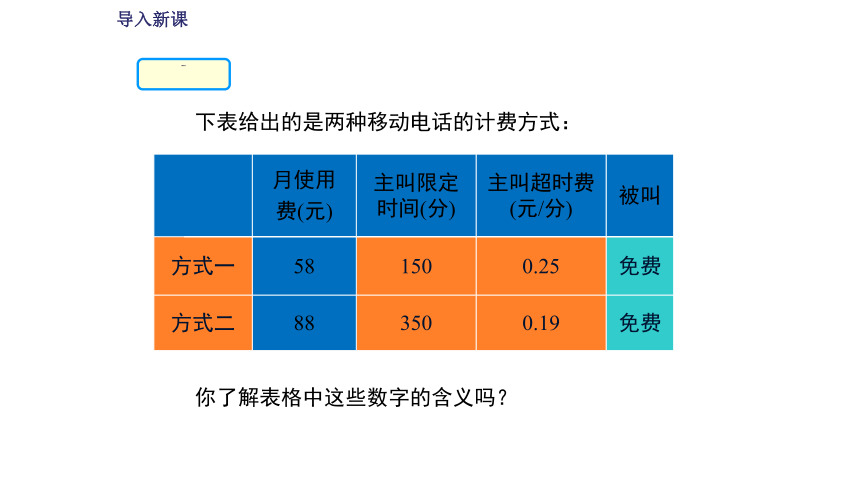
下表给出的是两种移动电话的计费方式:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用
费(元)
你了解表格中这些数字的含义吗?
讲授新课
电话计费问题
一
合作探究
你认为选择以下哪种计费方式更省钱呢?
350
0
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
150
计费方式一
计费方式二
350
哪种计费方式更省钱“与主叫时间有关”
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
结论:
问题:观察以上列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?
划算
划算
划算
(1)当t ≤150时,方式一计费少;
结论:
分析:设一个月内用移动电话主叫为t 分(t是正整数).根据t 在不同时间范围内取值,列表说明按方式一和方式二如何计费.
58
58
88
88
88
88
58+0.25(t-150)
58+0.25(350-150)=108
58+0.25(t-150)
88+0.19(t-350)
主叫时间t /分 方式一计费/元 方式二计费/元
t 大于150且小于 350 58+0.25(t-150) 88
(2)当150< t <350时,存在两种方式计费相等吗?
解:依题意,得 58+0.25(t-150) = 88
去括号,得 58+0.25t-37.5 = 88
移项、合并同类项,得 0.25t = 67.5
系数化1,得 t =270
当 t =270分时,两种计费方式的费用相等;
当270< t <350时,方式二计费少;
所以,当150< t <270时,方式一计费 少;
主叫时间t /分 方式一计费/元 方式二计费/元
t 等于350 108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
(4)当t >350分时,两种计费方式哪种更合算呢?
(3)当t =350分时,方式二计费少;
解:当t >350时,
方式一: 58+0.25(t-150)= 108+0.25(t-350)
方式二: 88+0.19(t-350)
所以,当t >350分时,方式二计费少;
划算
综合以上的分析,可以发现:
当t 时,选择方式一省钱;
当t 时,选择方式二省钱.
0
计费方式一
计费方式二
270
小于 270分
大于 270分
基本费58元
基本费88元
根据下面的两种移动电话计费方式表,考虑下列问题:
方式一 方式二
月租费 20元/月 0元
本地通话费 0.10元/分钟 0.20元/分钟
(1)对于本地通话时间,会出现按两种计费方式收费一样吗?
(2)请通过计算说明:什么情况下,使用方式一的电话合算?什么情况下,使用方式二的电话合算?
解:(1)设通话x分钟两种收费一样多,依题意得:
20+0.1x=0.2x 解得:x=200
答:当通话时间为200分钟时,两种计费方式一样。
课堂小结
1.电话计费问题的核心问题是“哪种计费方式更省钱与主叫时间有关”
2.解决电话计费问题的关键是找到两种计费方式花费相同时的时间是多少,然后进行分析
当堂练习
1.某地上网有两种收费方式,用户可以任选其一:A. 计
时制:0.5元/时 ; B. 包月制:50元/月.此外,每一种上网
方式都加收通讯费0.5元/时.(每月按30天计算)
(1)请你为用户设计一个方案,使用户能合理地选择上网
方式.
(2)某用户有120小时用于上网(1个月),选用哪种上网
方式比较合算?
答案:(1)当用户上网时间小于100小时,选择计时制;
当用户上网时间大于100小时,选择包月制.
(2)选择包月制上网方式合算.
解:设该用户每月上网时长为x小时,且此时两种方式收费一样
0.5x + 0.5x = 50 + 0.5x
x -0.5x = 50
x = 100
(1)当用户上网时间小于100小时,选择计时制;
当用户上网时间大于100小时,选择包月制.
(2)选择包月制上网方式合算.
2.某市为鼓励居民节约用水,对自来水用户按分段计费方式收取水费:若每户每月用水不超过7m3,则按2元/m3收费;若每户每月用水超过7m3,则超过的部分按3元/m3收费.如果某居民户去年12月缴纳了53元水费,那么这户居民去年12月的用水量为多少立方米?
因为2×7=14<53,所以该居民用水超过7m3
设该居民去年12月用水超过7m3 且超过部分为Xm3
解 14+3X=53
3X=39
X=13 X+7=20
答:这户居民去年12月的用水量为20立方米.
因为2×7=14<53,所以该居民用水超过7m3
设该居民去年12月用水为Xm3
解 14+3(X-7)=53
14+ 3X-21=53
3X=60
X=20
答:这户居民去年12月的用水量为20立方米.
要点梳理
一、方程的有关概念
1.方程:含有未知数的等式叫做方程.
2.一元一次方程的概念:只含有____个未知数,未知数的次数都是____,等号两边都是______,这样的方程叫做一元一次方程.
3.方程的解:使方程左右两边的值相等的未知数的值叫做方程的解,一元方程的解,也叫它的根.
4.解方程:求方程解的过程叫做解方程.
一
1
整式
2.常见的几种方程类型及等量关系:
(1)行程问题中基本量之间关系:路程=速度×时间.
①相遇问题:全路程=甲走的路程+乙走的路程;
②追及问题:甲为快者,被追路程=甲走路程-乙走路程;
③流水问题:v顺=v静+v水,v逆=v静-v水.
课堂小结
去括号
等式的性质
移项
合并同类项
方程的概念
概念
实际问题
去分母
系数化为1
解法步骤
方 程
一元一次方程
3.4 实际问题与一元一次方程
————球赛积分与电话费
复习 1.某家具厂生产一种方桌,1立方米的木材可做50个桌面或300条桌腿,现有10立方米的木材,怎样分配生产桌面和桌腿使用的木材,才能使桌面、桌腿刚好配套,共可生产多少张方桌?(一张方桌有1个桌面,4条桌腿)
解:设用x立方米的木材做桌面,则用(10-x)立方米的木材做桌腿.
根据题意,得4×50x=300(10-x),
解得 x=6,所以10-x=4,
可做方桌为50×6=300(张).
答:用6立方米的木材做桌面,4立方米的木材做桌腿,可做300张方桌.
学习目标
1.会阅读、理解表格,并从表格中提取关键信息.(重点)
2.掌握解决“球赛积分表问题”的一般思路,并会根据方程的解的情况对实际问题作出判断.(难点)
2000赛季篮球甲A联赛部分球队积分榜:
(1)列式表示积分与胜、负场数之间的数量关系;
(2)某队的胜场总积分能等于它的负场总积分吗
队名 比赛场次 胜场 负场 积分
八一双鹿 22 18 4 40
北京首钢 22 14 8 36
浙江万马 22 7 15 29
沈部雄狮 22 0 22 22
解:观察积分榜,从最下面一行可知负一场积1分.
设胜一场积x分,从表中其他任何一行可以列方程,求出x的值.例如,从第一行得出方程:
18x+1×4=40.
由此得出 x=2.
得出负一场积1分,胜一场积2分.
(1)如果一个队胜m场,则负(22-m)场,胜场积分为2m,负场积分为22-m,总积分为
2m+(22-m)=m+22.
(2)设一个队胜了x场,则负了(22-x)场,如果这个队的胜场总积分等于负场总积分,则有方程
2x=22-x
其中,x (胜场)的值必须是整数,所以 不符合实际.由此可以判定没有哪个队伍的胜场总积分等于负场总积分.
当堂练习
1.某球队参加比赛,开局9场保持不败,积21分,比赛规则:胜一场得3分,平一场得1分,则该队共胜( )
A.4场 B.5场 C.6场 D.7场
2.中国男篮CBA职业联赛的积分办法是:胜一场积2分,负一场积1分,某支球队参加了12场比赛,总积分恰是所胜场数的4倍,则该球队共胜____场.
C
4
学习目标
1.掌握解决“电话计费问题”的一般思路.(难点)
2.体验建立方程模型解决问题的一般过程.(重点)
导入新课
情境引入
下表给出的是两种移动电话的计费方式:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用
费(元)
你了解表格中这些数字的含义吗?
讲授新课
电话计费问题
一
合作探究
你认为选择以下哪种计费方式更省钱呢?
350
0
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
150
计费方式一
计费方式二
350
哪种计费方式更省钱“与主叫时间有关”
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
结论:
问题:观察以上列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?
划算
划算
划算
(1)当t ≤150时,方式一计费少;
结论:
分析:设一个月内用移动电话主叫为t 分(t是正整数).根据t 在不同时间范围内取值,列表说明按方式一和方式二如何计费.
58
58
88
88
88
88
58+0.25(t-150)
58+0.25(350-150)=108
58+0.25(t-150)
88+0.19(t-350)
主叫时间t /分 方式一计费/元 方式二计费/元
t 大于150且小于 350 58+0.25(t-150) 88
(2)当150< t <350时,存在两种方式计费相等吗?
解:依题意,得 58+0.25(t-150) = 88
去括号,得 58+0.25t-37.5 = 88
移项、合并同类项,得 0.25t = 67.5
系数化1,得 t =270
当 t =270分时,两种计费方式的费用相等;
当270< t <350时,方式二计费少;
所以,当150< t <270时,方式一计费 少;
主叫时间t /分 方式一计费/元 方式二计费/元
t 等于350 108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
(4)当t >350分时,两种计费方式哪种更合算呢?
(3)当t =350分时,方式二计费少;
解:当t >350时,
方式一: 58+0.25(t-150)= 108+0.25(t-350)
方式二: 88+0.19(t-350)
所以,当t >350分时,方式二计费少;
划算
综合以上的分析,可以发现:
当t 时,选择方式一省钱;
当t 时,选择方式二省钱.
0
计费方式一
计费方式二
270
小于 270分
大于 270分
基本费58元
基本费88元
根据下面的两种移动电话计费方式表,考虑下列问题:
方式一 方式二
月租费 20元/月 0元
本地通话费 0.10元/分钟 0.20元/分钟
(1)对于本地通话时间,会出现按两种计费方式收费一样吗?
(2)请通过计算说明:什么情况下,使用方式一的电话合算?什么情况下,使用方式二的电话合算?
解:(1)设通话x分钟两种收费一样多,依题意得:
20+0.1x=0.2x 解得:x=200
答:当通话时间为200分钟时,两种计费方式一样。
课堂小结
1.电话计费问题的核心问题是“哪种计费方式更省钱与主叫时间有关”
2.解决电话计费问题的关键是找到两种计费方式花费相同时的时间是多少,然后进行分析
当堂练习
1.某地上网有两种收费方式,用户可以任选其一:A. 计
时制:0.5元/时 ; B. 包月制:50元/月.此外,每一种上网
方式都加收通讯费0.5元/时.(每月按30天计算)
(1)请你为用户设计一个方案,使用户能合理地选择上网
方式.
(2)某用户有120小时用于上网(1个月),选用哪种上网
方式比较合算?
答案:(1)当用户上网时间小于100小时,选择计时制;
当用户上网时间大于100小时,选择包月制.
(2)选择包月制上网方式合算.
解:设该用户每月上网时长为x小时,且此时两种方式收费一样
0.5x + 0.5x = 50 + 0.5x
x -0.5x = 50
x = 100
(1)当用户上网时间小于100小时,选择计时制;
当用户上网时间大于100小时,选择包月制.
(2)选择包月制上网方式合算.
2.某市为鼓励居民节约用水,对自来水用户按分段计费方式收取水费:若每户每月用水不超过7m3,则按2元/m3收费;若每户每月用水超过7m3,则超过的部分按3元/m3收费.如果某居民户去年12月缴纳了53元水费,那么这户居民去年12月的用水量为多少立方米?
因为2×7=14<53,所以该居民用水超过7m3
设该居民去年12月用水超过7m3 且超过部分为Xm3
解 14+3X=53
3X=39
X=13 X+7=20
答:这户居民去年12月的用水量为20立方米.
因为2×7=14<53,所以该居民用水超过7m3
设该居民去年12月用水为Xm3
解 14+3(X-7)=53
14+ 3X-21=53
3X=60
X=20
答:这户居民去年12月的用水量为20立方米.
要点梳理
一、方程的有关概念
1.方程:含有未知数的等式叫做方程.
2.一元一次方程的概念:只含有____个未知数,未知数的次数都是____,等号两边都是______,这样的方程叫做一元一次方程.
3.方程的解:使方程左右两边的值相等的未知数的值叫做方程的解,一元方程的解,也叫它的根.
4.解方程:求方程解的过程叫做解方程.
一
1
整式
2.常见的几种方程类型及等量关系:
(1)行程问题中基本量之间关系:路程=速度×时间.
①相遇问题:全路程=甲走的路程+乙走的路程;
②追及问题:甲为快者,被追路程=甲走路程-乙走路程;
③流水问题:v顺=v静+v水,v逆=v静-v水.
课堂小结
去括号
等式的性质
移项
合并同类项
方程的概念
概念
实际问题
去分母
系数化为1
解法步骤
方 程
一元一次方程
