5.3 平行线的判定和性质复习课件
文档属性
| 名称 | 5.3 平行线的判定和性质复习课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 164.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-07 00:00:00 | ||
图片预览

文档简介
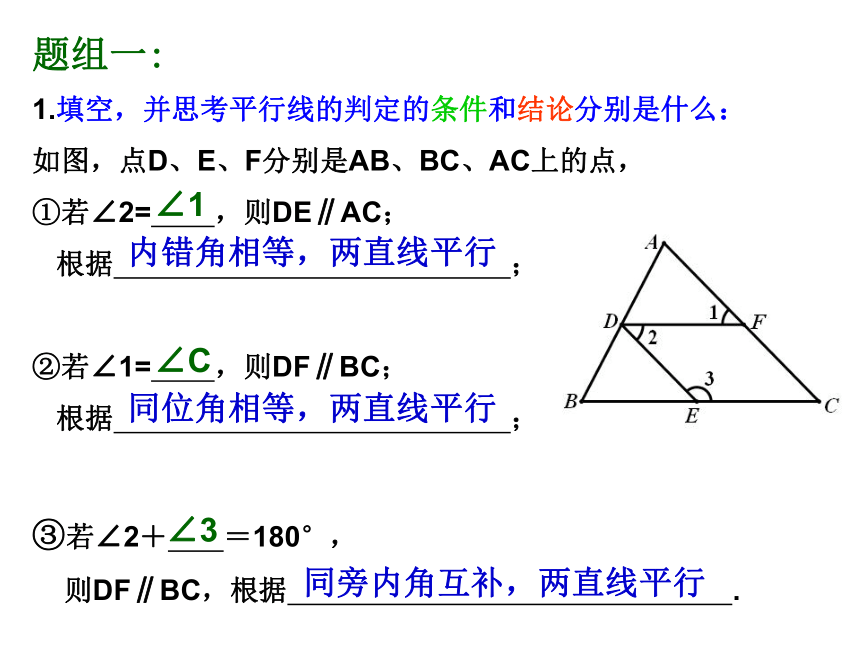
课件22张PPT。§5.3 平行线的判定和性质复习题组一: 1.填空,并思考平行线的判定的条件和结论分别是什么:
如图,点D、E、F分别是AB、BC、AC上的点,
①若∠2= ,则DE∥AC;
根据 ;
②若∠1= ,则DF∥BC;
根据 ;
③若∠2+ =180°,
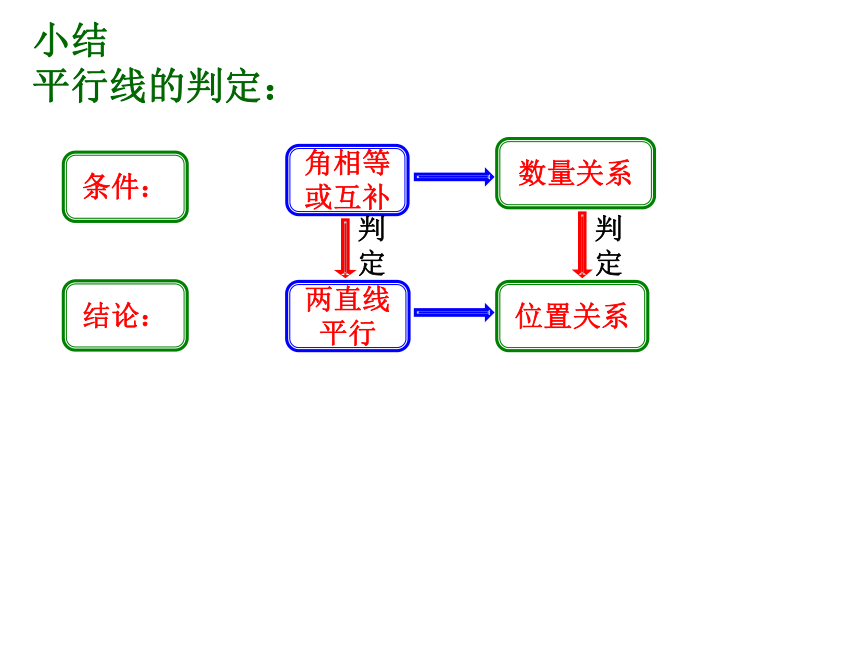
则DF∥BC,根据 . ∠1∠C∠3内错角相等,两直线平行同位角相等,两直线平行同旁内角互补,两直线平行条件:小结
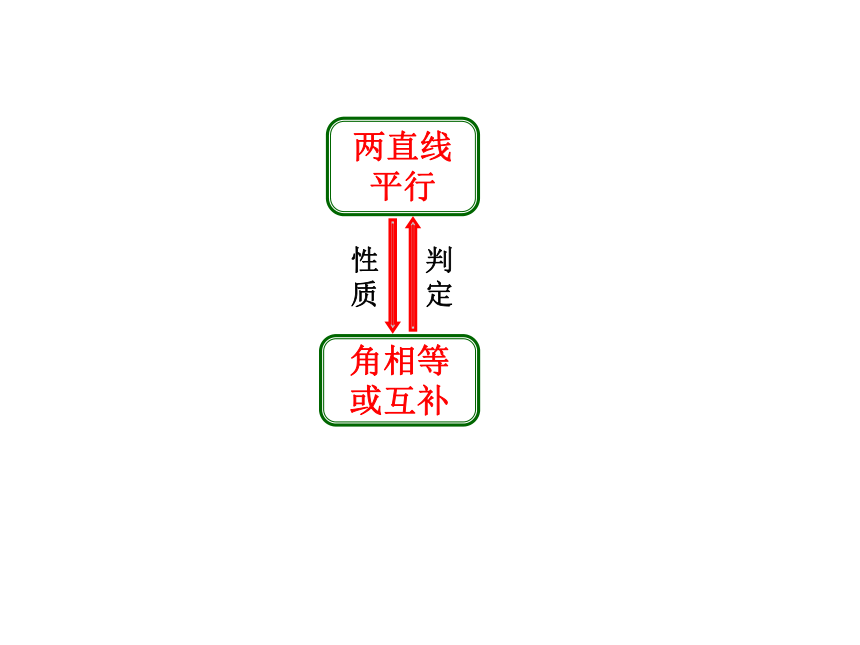
平行线的判定: 数量关系位置关系结论:角相等或互补两直线平行判定判定2.填空,并思考平行线的性质的条件和结论分别是什么:
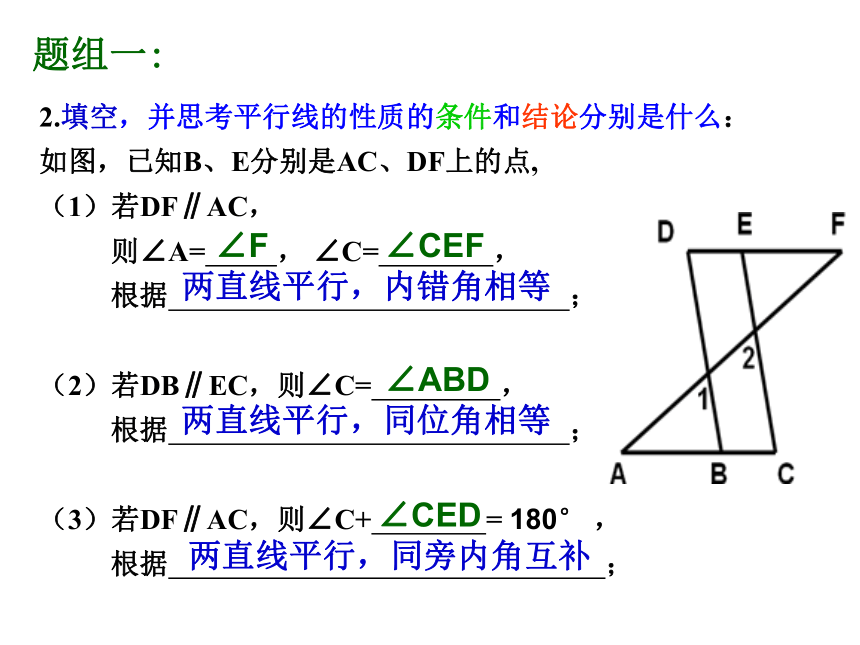
如图,已知B、E分别是AC、DF上的点,
(1)若DF∥AC,
则∠A= , ∠C= ,
根据 ;
(2)若DB∥EC,则∠C= ,
根据 ;
(3)若DF∥AC,则∠C+ = 180° ,
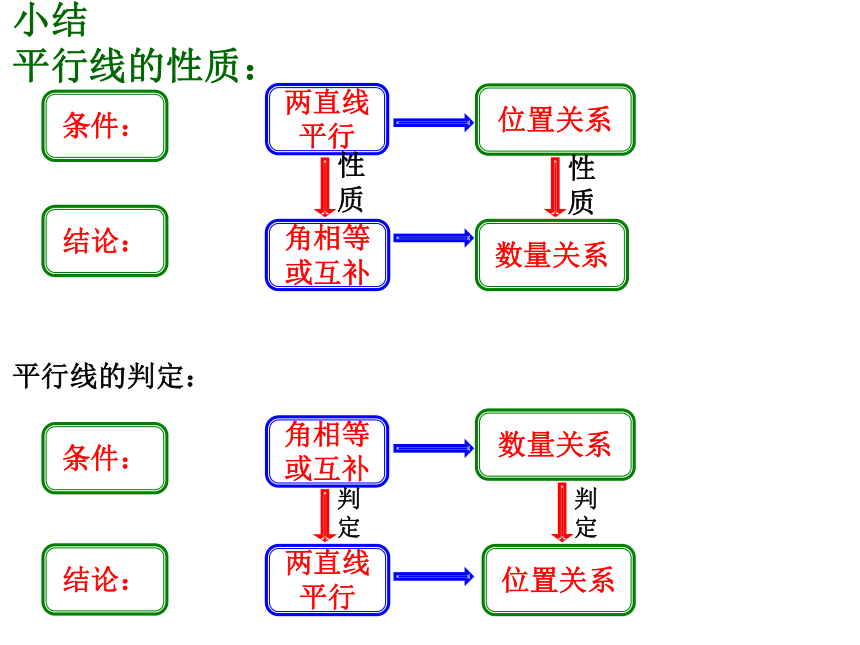
根据 ;题组一: ∠F∠CEF∠ABD两直线平行,内错角相等两直线平行,同位角相等两直线平行,同旁内角互补∠CED条件:小结
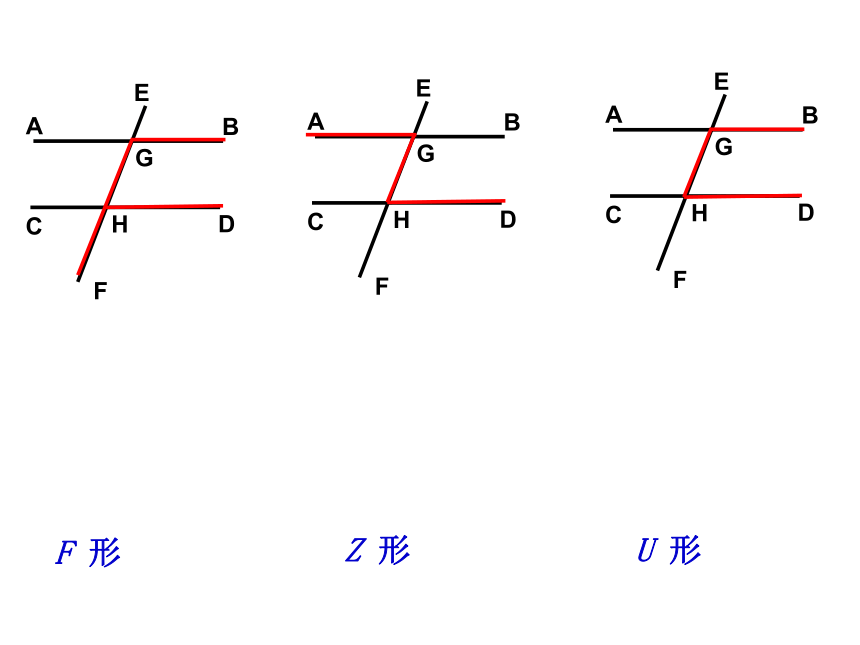
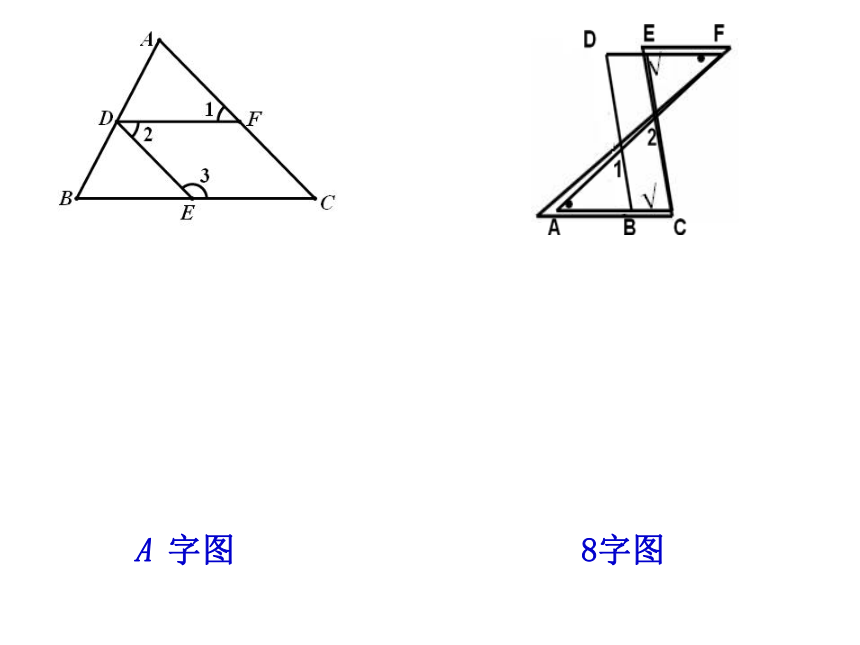
平行线的性质: 位置关系数量关系结论:两直线平行角相等或互补 条件:平行线的判定: 数量关系位置关系结论:角相等或互补两直线平行性质性质判定判定两直线平行角相等或互补性质判定F 形Z 形U 形A 字图8字图题组二: 1.填空:
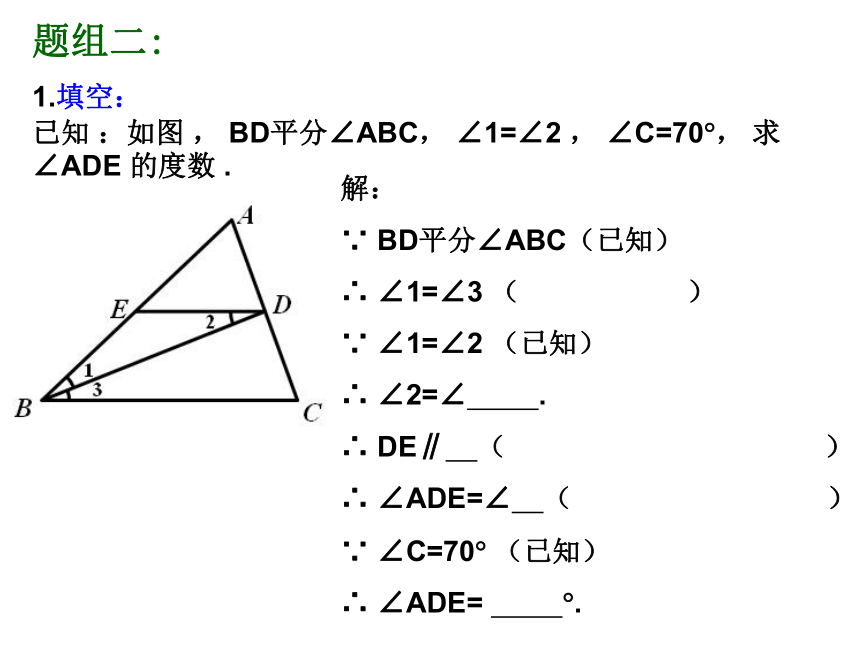
已知 :如图 , BD平分∠ABC, ∠1=∠2 , ∠C=70?, 求∠ADE 的度数 .
解:
∵ BD平分∠ABC(已知)
∴ ∠1=∠3 ( )
∵ ∠1=∠2 (已知)
∴ ∠2=∠ .
∴ DE∥ ( )
∴ ∠ADE=∠ ( )
∵ ∠C=70? (已知)
∴ ∠ADE= ?.题组二: 2.如图,若AB∥DF,∠1=∠A,试确定DE与AC的位置关系,
并说明理由. 题组二: 3.已知:如图,AE、DF分别与GC相交于点B、C, ∠BAD=∠BCD, ∠1=∠2,求证:∠3=∠4. 两直线平行角相等或互补性质判定解题思路总结:两直线平行角相等或互补判定两直线平行角相等或互补性质题组三: 1.填空:
已知:如图,DB∥EC,∠C=∠D,求证:∠A=∠F.
证明:
∵ DB∥EC(已知)
∴ ∠C= ∠ ( )
∵ ∠C=∠D (已知)
∴ ∠D = ∠ .
∴ AB ∥ ( )
∴ ∠A=∠F ( )分析:要证∠A=∠F,需证 ,再需证 ;结合条件∠C=∠D,需证 . 题组三: 变式:
已知:如图,∠1=∠2, ∠C=∠D,求证:∠A=∠F. 题组三: 2.已知:如图,DE∥BC,∠1=∠B,∠3和∠4的度数之间
有什么关系,说明你的理由.题组三: 变式:
已知:如图,∠3+∠4=180 ? ,∠1=∠B, DE和BC之间
有什么样的位置关系,说明你的理由.两直线平行角相等或互补性质判定解题思路总结:两直线平行角相等或互补判定两直线平行角相等或互补性质角相等或互补两直线平行性质判定数形数形结合数形位置关系角相等或互补两直线平行数形数形结合数量
关系本课小结:检测:1.如图,EF∥AD,∠1 =∠2,∠BAC = 70°.
将求∠AGD的过程填写完整.
∵EF∥AD,( )
∴ ∠2 = .( )
又∵ ∠1 = ∠2,( )
∴ ∠1 = ∠3.
∴AB∥ .( )
∴∠BAC + = 180°.( )
又∵∠BAC = 70°,( )
∴∠AGD = °.
检测:2.已知:如图,∠1=∠C,∠2=44°,求∠3的度数.位置关系数量关系
角相等或互补直线平行角相等或互补直线平行数形数形结合数量关系位置关系
如图,点D、E、F分别是AB、BC、AC上的点,
①若∠2= ,则DE∥AC;
根据 ;
②若∠1= ,则DF∥BC;
根据 ;
③若∠2+ =180°,
则DF∥BC,根据 . ∠1∠C∠3内错角相等,两直线平行同位角相等,两直线平行同旁内角互补,两直线平行条件:小结
平行线的判定: 数量关系位置关系结论:角相等或互补两直线平行判定判定2.填空,并思考平行线的性质的条件和结论分别是什么:
如图,已知B、E分别是AC、DF上的点,
(1)若DF∥AC,
则∠A= , ∠C= ,
根据 ;
(2)若DB∥EC,则∠C= ,
根据 ;
(3)若DF∥AC,则∠C+ = 180° ,
根据 ;题组一: ∠F∠CEF∠ABD两直线平行,内错角相等两直线平行,同位角相等两直线平行,同旁内角互补∠CED条件:小结
平行线的性质: 位置关系数量关系结论:两直线平行角相等或互补 条件:平行线的判定: 数量关系位置关系结论:角相等或互补两直线平行性质性质判定判定两直线平行角相等或互补性质判定F 形Z 形U 形A 字图8字图题组二: 1.填空:
已知 :如图 , BD平分∠ABC, ∠1=∠2 , ∠C=70?, 求∠ADE 的度数 .
解:
∵ BD平分∠ABC(已知)
∴ ∠1=∠3 ( )
∵ ∠1=∠2 (已知)
∴ ∠2=∠ .
∴ DE∥ ( )
∴ ∠ADE=∠ ( )
∵ ∠C=70? (已知)
∴ ∠ADE= ?.题组二: 2.如图,若AB∥DF,∠1=∠A,试确定DE与AC的位置关系,
并说明理由. 题组二: 3.已知:如图,AE、DF分别与GC相交于点B、C, ∠BAD=∠BCD, ∠1=∠2,求证:∠3=∠4. 两直线平行角相等或互补性质判定解题思路总结:两直线平行角相等或互补判定两直线平行角相等或互补性质题组三: 1.填空:
已知:如图,DB∥EC,∠C=∠D,求证:∠A=∠F.
证明:
∵ DB∥EC(已知)
∴ ∠C= ∠ ( )
∵ ∠C=∠D (已知)
∴ ∠D = ∠ .
∴ AB ∥ ( )
∴ ∠A=∠F ( )分析:要证∠A=∠F,需证 ,再需证 ;结合条件∠C=∠D,需证 . 题组三: 变式:
已知:如图,∠1=∠2, ∠C=∠D,求证:∠A=∠F. 题组三: 2.已知:如图,DE∥BC,∠1=∠B,∠3和∠4的度数之间
有什么关系,说明你的理由.题组三: 变式:
已知:如图,∠3+∠4=180 ? ,∠1=∠B, DE和BC之间
有什么样的位置关系,说明你的理由.两直线平行角相等或互补性质判定解题思路总结:两直线平行角相等或互补判定两直线平行角相等或互补性质角相等或互补两直线平行性质判定数形数形结合数形位置关系角相等或互补两直线平行数形数形结合数量
关系本课小结:检测:1.如图,EF∥AD,∠1 =∠2,∠BAC = 70°.
将求∠AGD的过程填写完整.
∵EF∥AD,( )
∴ ∠2 = .( )
又∵ ∠1 = ∠2,( )
∴ ∠1 = ∠3.
∴AB∥ .( )
∴∠BAC + = 180°.( )
又∵∠BAC = 70°,( )
∴∠AGD = °.
检测:2.已知:如图,∠1=∠C,∠2=44°,求∠3的度数.位置关系数量关系
角相等或互补直线平行角相等或互补直线平行数形数形结合数量关系位置关系
