3.2.1 合并同类项解方程及应用 课件(共20张PPT)
文档属性
| 名称 | 3.2.1 合并同类项解方程及应用 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 951.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
3.2 合并同类项与移项
第三章 一元一次方程
第1课时 合并同类项解方程及应用
精品同步教学课件
教学目标
1. 学会运用合并同类项解形如ax+bx=c类型的一元一次方程,进一步体会方程中的“化归”思想.
2. 能够根据题意找出实际问题中的相等关系,列出方程求解.
重点:学会运用合并同类项解形如ax+bx=c类型的一元一次方程
难点:能够根据题意找出实际问题中的相等关系,列出方程求解.
核心素养:培养运算能力
用合并同类项解一元一次方程的步骤
第一步:合并同类项,即将等号同侧的含未知数的项、常数项分别合并,把方程转化为ax=b(a ≠ 0)的形式.
第二步:系数化为1,即在方程两边同时除以一次项系数a,将一次项系数化为1,得到x= .
例 1
解下列一元一次方程.
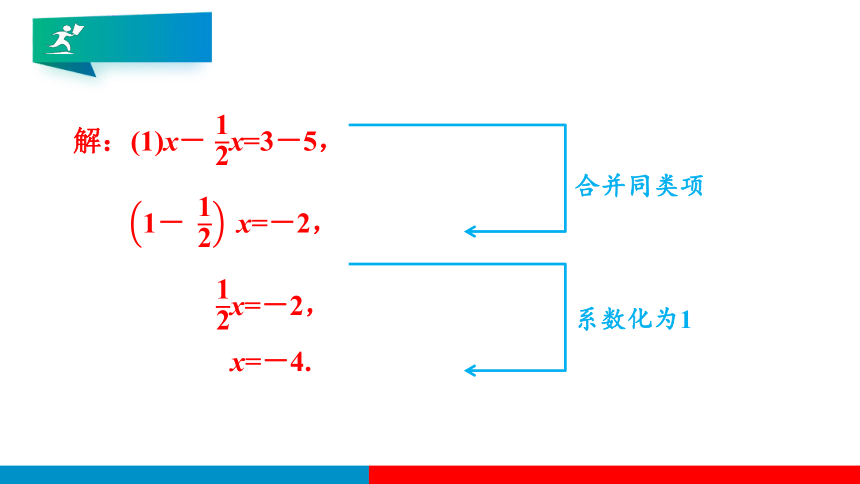
(1)x- x=3-5;(2)-2x-7x+8x=-15×2-6×3.
解题秘方:利用合并同类项的法则,将方程左右两边同时合并同类项,然后将未知数的系数化为1.
解:(1)x- x=3-5,
x=-2,
x=-2,
x=-4.
合并同类项
系数化为1
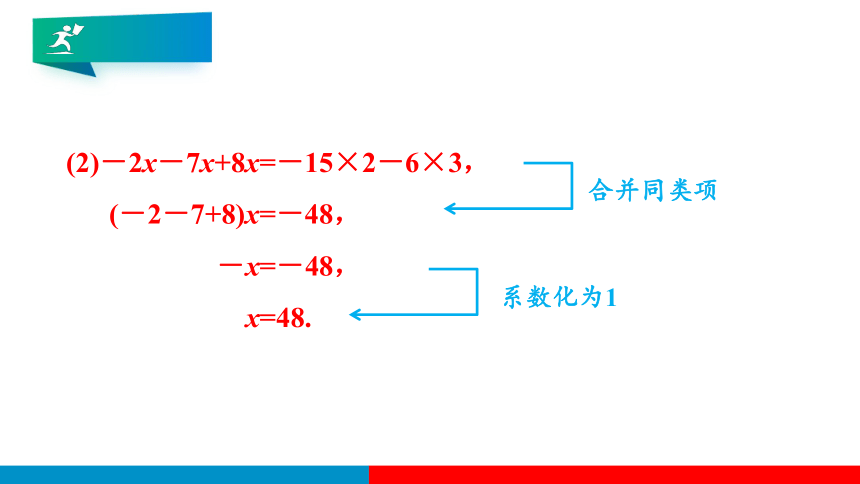
(2)-2x-7x+8x=-15×2-6×3,
(-2-7+8)x=-48,
-x=-48,
x=48.
合并同类项
系数化为1
练习:解下列方程:
(1)4x-3x=1 ; (2)-x+4x=6-1;
解: x= 1
3x= 5
x=
(3)- =-2; (4)-2x+0.5x=1.
解: = -2
x= -12
-1.5x= 1
x= -
某校七年级200 名学生分别到甲、乙两个纪念馆参观,其中到甲纪念馆参观的学生人数比到乙纪念馆参观的学生人数的2 倍少10 名,求到乙纪念馆参观的学生有多少名.
解题秘方:用分量的和等于总量列出方程,解决问题.
例2
解:设到乙纪念馆参观的学生有x 名,则到甲纪念馆参观的学生有(2x-10)名. 根据题意,可得2x-10+x=200.
解得x=70.
答:到乙纪念馆参观的学生有70 名.
练习. 某厂1 月份的产量为a 吨,2 月份的产量比1 月份增加了2 倍,3 月份的产量比2 月份增加了1 倍,如果第一季度的产量为1 800 吨,求1 月份的产量是多少.
解:由题意,得1月份的产量为a吨,
2月份的产量为a+2a=3a(吨),3月份的产量为2×3a=6a(吨),所以a+3a+6a=1 800.
合并同类项,得10a=1 800.
系数化为1,得a=180.
答:1月份的产量为180吨.
例3 有一列数,按一定规律排列成1,-3,9,-27,81,-243 ,··· . 其中某三个相邻数的和是-1701,这三个数各是多少?
从符号和绝对值两方面观察,可发现这列数的排列规律:后面的数是它前面的数与-3的乘积.如果三个相邻数中的第1个数记为x,则后两个数分别是-3x,9x.
提示
由三个数的和是-1701,得
合并同类项,得
系数化为1,得
解:设所求的三个数分别是 .
答:这三个数是 -243,729,-2187.
所以
例4 足球表面是由若干个黑色五边形和白色六边形皮块围成的,黑、白皮块数目的比为3:5,一个足球表面一共有32个皮块,黑色皮块和白色皮块各有多少个?
解:设黑色皮块有3x个,则白色皮块有5x个.
根据题意列方程 3x + 5x = 32,
解得 x = 4,
则黑色皮块有 3x = 12 (个),白色皮块有 5x = 20 (个).
答:黑色皮块有12个,白色皮块有20个.
你还能举出 总量=各部分量之和 的例子吗?
班级总人数=男生+女生
买文具的总数=买铅笔的钱+买中性笔的钱
产品的总数量=A种产品数量+B种产品数量+C种产品数量
方法归纳:当题目中出现比例时,一般可通过间接设元,设其中的每一份为x,然后用含x的代数式表示各数量,根据等量关系,列方程求解.
题目条件类型:
1.谁比谁多(少):甲比乙多20
2.谁比谁的几倍:甲是乙的2倍少2
3.告诉甲乙丙的比例:甲乙丙的比例是1:2:3
练习:某洗衣厂2019年计划生产洗衣机25500台,其中Ⅰ型、Ⅱ型、Ⅲ型三种洗衣机的数量之比为1:2:14,这三种洗衣机计划各生产多少台
答:计划生产Ⅰ型洗衣机1500台,Ⅱ型洗衣机3000台,Ⅲ型洗衣机21000台.
解:设计划生产Ⅰ型洗衣机x台,则计划生产Ⅱ型洗衣机2x台,Ⅲ型洗衣机14x台,依题意,得
x+2x+14x=25500,
解得x=1500,
则2x=3000,14x=21000.
https://www.21cnjy.com/help/help_extract.php
3.2 合并同类项与移项
第三章 一元一次方程
第1课时 合并同类项解方程及应用
精品同步教学课件
教学目标
1. 学会运用合并同类项解形如ax+bx=c类型的一元一次方程,进一步体会方程中的“化归”思想.
2. 能够根据题意找出实际问题中的相等关系,列出方程求解.
重点:学会运用合并同类项解形如ax+bx=c类型的一元一次方程
难点:能够根据题意找出实际问题中的相等关系,列出方程求解.
核心素养:培养运算能力
用合并同类项解一元一次方程的步骤
第一步:合并同类项,即将等号同侧的含未知数的项、常数项分别合并,把方程转化为ax=b(a ≠ 0)的形式.
第二步:系数化为1,即在方程两边同时除以一次项系数a,将一次项系数化为1,得到x= .
例 1
解下列一元一次方程.
(1)x- x=3-5;(2)-2x-7x+8x=-15×2-6×3.
解题秘方:利用合并同类项的法则,将方程左右两边同时合并同类项,然后将未知数的系数化为1.
解:(1)x- x=3-5,
x=-2,
x=-2,
x=-4.
合并同类项
系数化为1
(2)-2x-7x+8x=-15×2-6×3,
(-2-7+8)x=-48,
-x=-48,
x=48.
合并同类项
系数化为1
练习:解下列方程:
(1)4x-3x=1 ; (2)-x+4x=6-1;
解: x= 1
3x= 5
x=
(3)- =-2; (4)-2x+0.5x=1.
解: = -2
x= -12
-1.5x= 1
x= -
某校七年级200 名学生分别到甲、乙两个纪念馆参观,其中到甲纪念馆参观的学生人数比到乙纪念馆参观的学生人数的2 倍少10 名,求到乙纪念馆参观的学生有多少名.
解题秘方:用分量的和等于总量列出方程,解决问题.
例2
解:设到乙纪念馆参观的学生有x 名,则到甲纪念馆参观的学生有(2x-10)名. 根据题意,可得2x-10+x=200.
解得x=70.
答:到乙纪念馆参观的学生有70 名.
练习. 某厂1 月份的产量为a 吨,2 月份的产量比1 月份增加了2 倍,3 月份的产量比2 月份增加了1 倍,如果第一季度的产量为1 800 吨,求1 月份的产量是多少.
解:由题意,得1月份的产量为a吨,
2月份的产量为a+2a=3a(吨),3月份的产量为2×3a=6a(吨),所以a+3a+6a=1 800.
合并同类项,得10a=1 800.
系数化为1,得a=180.
答:1月份的产量为180吨.
例3 有一列数,按一定规律排列成1,-3,9,-27,81,-243 ,··· . 其中某三个相邻数的和是-1701,这三个数各是多少?
从符号和绝对值两方面观察,可发现这列数的排列规律:后面的数是它前面的数与-3的乘积.如果三个相邻数中的第1个数记为x,则后两个数分别是-3x,9x.
提示
由三个数的和是-1701,得
合并同类项,得
系数化为1,得
解:设所求的三个数分别是 .
答:这三个数是 -243,729,-2187.
所以
例4 足球表面是由若干个黑色五边形和白色六边形皮块围成的,黑、白皮块数目的比为3:5,一个足球表面一共有32个皮块,黑色皮块和白色皮块各有多少个?
解:设黑色皮块有3x个,则白色皮块有5x个.
根据题意列方程 3x + 5x = 32,
解得 x = 4,
则黑色皮块有 3x = 12 (个),白色皮块有 5x = 20 (个).
答:黑色皮块有12个,白色皮块有20个.
你还能举出 总量=各部分量之和 的例子吗?
班级总人数=男生+女生
买文具的总数=买铅笔的钱+买中性笔的钱
产品的总数量=A种产品数量+B种产品数量+C种产品数量
方法归纳:当题目中出现比例时,一般可通过间接设元,设其中的每一份为x,然后用含x的代数式表示各数量,根据等量关系,列方程求解.
题目条件类型:
1.谁比谁多(少):甲比乙多20
2.谁比谁的几倍:甲是乙的2倍少2
3.告诉甲乙丙的比例:甲乙丙的比例是1:2:3
练习:某洗衣厂2019年计划生产洗衣机25500台,其中Ⅰ型、Ⅱ型、Ⅲ型三种洗衣机的数量之比为1:2:14,这三种洗衣机计划各生产多少台
答:计划生产Ⅰ型洗衣机1500台,Ⅱ型洗衣机3000台,Ⅲ型洗衣机21000台.
解:设计划生产Ⅰ型洗衣机x台,则计划生产Ⅱ型洗衣机2x台,Ⅲ型洗衣机14x台,依题意,得
x+2x+14x=25500,
解得x=1500,
则2x=3000,14x=21000.
https://www.21cnjy.com/help/help_extract.php
