3.3 第2课时 去分母解方程 课件(共21张PPT)
文档属性
| 名称 | 3.3 第2课时 去分母解方程 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-12 16:02:19 | ||
图片预览








文档简介
(共21张PPT)
3.3 解一元一次方程(二)
——去括号与去分母
第三章 一元一次方程
第2课时 利用去分母解一元一次方程
精品同步教学课件
教学目标
1. 掌握含有分数系数的一元一次方程的解法.
2. 熟练利用解一元一次方程的步骤解各种类型的方程.
重点:掌握含有分数系数的一元一次方程的解法.
难点:熟练利用解一元一次方程的步骤解各种类型的方程.
核心素养:培养运算能力
解含分母的一元一次方程
一
2. 去分母时要注意什么问题
想一想
1. 若使方程的系数变成整数系数方程,
方程两边应该同乘以什么数
解方程:
1. 解含有分母的一元一次方程时,方程两边乘各分母的最小公倍数,从而约去分母,这个过程叫做去分母.
2. 解一元一次方程的步骤
(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)系数化为1.
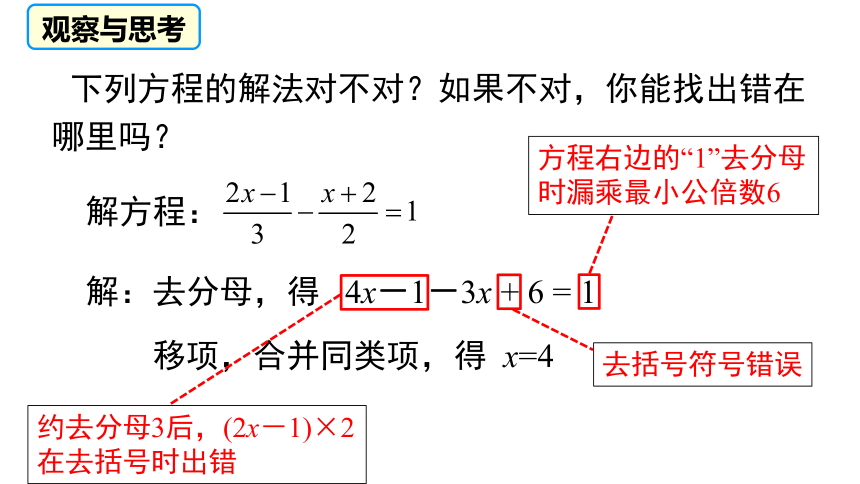
下列方程的解法对不对?如果不对,你能找出错在哪里吗?
解方程:
解:去分母,得 4x-1-3x + 6 = 1
移项,合并同类项,得 x=4
观察与思考
方程右边的“1”去分母时漏乘最小公倍数6
去括号符号错误
约去分母3后,(2x-1)×2在去括号时出错
例1
解下列一元一次方程: +4= - .
解题秘方:按“去分母→去括号→移项→合并同类项→系数化为1”的步骤解方程.
解: +4= - .
去分母(方程两边乘6),得2(x+5)+24=3(x+3)-(5x-2).
去括号,得2x+10+24=3x+9-5x+2.
移项,得2x-3x+5x=9+2-10-24.
合并同类项,得4x=-23.
系数化为1,得x=- .
练习: 解下列方程:
(1)= ; (2) +1= ;
解:3(x-1)= 5x,
3x-3= 5x,
-2x= 3,
x= -.
x+3= 2x+1,
x-2x= 1-3,
-x= -2,
x= 2.
(3)- =-2;
解:5(x+2)-3(2x-3)=-30,
5x+10-6x+9= -30,
-x= -30-10-9,
x= 49.
(4)2- = .
解:12-2(2x+1)= 3(1+x),
12-4x-2= 3+3x,
-4x-3x= 3-12+2,
-7x= -7,
x= 1.
练习. 解下列方程:
(1)(1- )=- x+1; (2)+ 1 =;
解:x=
x=
(3)-(3x+4)=-;
x=
(4)3x + = 3- ; (5)x+ = -x;
(6)-x = -1.
解:x=
x=2
x=-
练习. 如果的值比的值大1,求2-a的值.
解:由题意,得- =1.
去分母,得7(a+3)-4(2a-3)=28.
去括号,得7a+21-8a+12=28.
移项、合并同类项,得-a=-5.
系数化为1,得a=5.所以2-a=2-5=-3.
在一次爱心捐款活动中,育才中学七年级一班捐款数为七年级三个班总捐款数的,二班捐款数为一班、三班捐款数的和的一半,三班捐了980 元,求七年级三个班总捐款数.
例 2
解:设七年级一班捐款数为x元,那么二班捐款数为(x+980)元,三个班总捐款数为3x 元.
由题意,得x+ (x+980)+980=3x,
解得x=980. 所以3x=3×980=2 940.
答:七年级三个班总捐款数为2 940 元.
练习. [中考· 武汉] 我国古代数学名著《九章算术》
中记载“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”意思是:现有几个人共买一件物品,每人出8 钱,多出3 钱;每人出7 钱,还差4钱.问人数、物价各是多少?若设共有x 人,物价是y 钱,则下列方程正确的是( )
A. 8(x-3)= 7(x+4) B. 8x+3 = 7x-4
C. = D. =
D
练习 有一人问老师,他所教的班级有多少学生,老师说:“一半学生在学数学,四分之一的学生在学音乐,七分之一的学生在学外语,还剩六位学生正在操场踢足球.”你知道这个班有多少学生吗?
答:这个班有56个学生.
解:这个班有x名学生,依题意得
解得x=56.
1. 去分母时,应在方程的左右两边乘以分母
的 ;
2. 去分母的依据是 ,去分母时不能
漏乘 ;
3. 去分母与去括号这两步分开写,不要跳步,
防止忘记变号.
最小公倍数
等式性质2
没有分母的项
要点归纳
趣味拓展
丢番图的墓志铭:
“坟中安葬着丢番图,多么令人惊讶,它忠实地记录了所经历的道路.上帝给予的童年占六分之一.又过十二分之一,两颊长胡.再过七分之一,点燃结婚的蜡烛.五年之后天赐贵子,可怜迟到的宁馨儿,享年仅及其父之半,便进入冰冷的墓.悲伤只有用数论的研究去弥补,又过四年,他也走完了人生的旅途.”
你知道丢番图去世时的年龄吗 请你列出方程
来算一算.
思考
https://www.21cnjy.com/help/help_extract.php
3.3 解一元一次方程(二)
——去括号与去分母
第三章 一元一次方程
第2课时 利用去分母解一元一次方程
精品同步教学课件
教学目标
1. 掌握含有分数系数的一元一次方程的解法.
2. 熟练利用解一元一次方程的步骤解各种类型的方程.
重点:掌握含有分数系数的一元一次方程的解法.
难点:熟练利用解一元一次方程的步骤解各种类型的方程.
核心素养:培养运算能力
解含分母的一元一次方程
一
2. 去分母时要注意什么问题
想一想
1. 若使方程的系数变成整数系数方程,
方程两边应该同乘以什么数
解方程:
1. 解含有分母的一元一次方程时,方程两边乘各分母的最小公倍数,从而约去分母,这个过程叫做去分母.
2. 解一元一次方程的步骤
(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)系数化为1.
下列方程的解法对不对?如果不对,你能找出错在哪里吗?
解方程:
解:去分母,得 4x-1-3x + 6 = 1
移项,合并同类项,得 x=4
观察与思考
方程右边的“1”去分母时漏乘最小公倍数6
去括号符号错误
约去分母3后,(2x-1)×2在去括号时出错
例1
解下列一元一次方程: +4= - .
解题秘方:按“去分母→去括号→移项→合并同类项→系数化为1”的步骤解方程.
解: +4= - .
去分母(方程两边乘6),得2(x+5)+24=3(x+3)-(5x-2).
去括号,得2x+10+24=3x+9-5x+2.
移项,得2x-3x+5x=9+2-10-24.
合并同类项,得4x=-23.
系数化为1,得x=- .
练习: 解下列方程:
(1)= ; (2) +1= ;
解:3(x-1)= 5x,
3x-3= 5x,
-2x= 3,
x= -.
x+3= 2x+1,
x-2x= 1-3,
-x= -2,
x= 2.
(3)- =-2;
解:5(x+2)-3(2x-3)=-30,
5x+10-6x+9= -30,
-x= -30-10-9,
x= 49.
(4)2- = .
解:12-2(2x+1)= 3(1+x),
12-4x-2= 3+3x,
-4x-3x= 3-12+2,
-7x= -7,
x= 1.
练习. 解下列方程:
(1)(1- )=- x+1; (2)+ 1 =;
解:x=
x=
(3)-(3x+4)=-;
x=
(4)3x + = 3- ; (5)x+ = -x;
(6)-x = -1.
解:x=
x=2
x=-
练习. 如果的值比的值大1,求2-a的值.
解:由题意,得- =1.
去分母,得7(a+3)-4(2a-3)=28.
去括号,得7a+21-8a+12=28.
移项、合并同类项,得-a=-5.
系数化为1,得a=5.所以2-a=2-5=-3.
在一次爱心捐款活动中,育才中学七年级一班捐款数为七年级三个班总捐款数的,二班捐款数为一班、三班捐款数的和的一半,三班捐了980 元,求七年级三个班总捐款数.
例 2
解:设七年级一班捐款数为x元,那么二班捐款数为(x+980)元,三个班总捐款数为3x 元.
由题意,得x+ (x+980)+980=3x,
解得x=980. 所以3x=3×980=2 940.
答:七年级三个班总捐款数为2 940 元.
练习. [中考· 武汉] 我国古代数学名著《九章算术》
中记载“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”意思是:现有几个人共买一件物品,每人出8 钱,多出3 钱;每人出7 钱,还差4钱.问人数、物价各是多少?若设共有x 人,物价是y 钱,则下列方程正确的是( )
A. 8(x-3)= 7(x+4) B. 8x+3 = 7x-4
C. = D. =
D
练习 有一人问老师,他所教的班级有多少学生,老师说:“一半学生在学数学,四分之一的学生在学音乐,七分之一的学生在学外语,还剩六位学生正在操场踢足球.”你知道这个班有多少学生吗?
答:这个班有56个学生.
解:这个班有x名学生,依题意得
解得x=56.
1. 去分母时,应在方程的左右两边乘以分母
的 ;
2. 去分母的依据是 ,去分母时不能
漏乘 ;
3. 去分母与去括号这两步分开写,不要跳步,
防止忘记变号.
最小公倍数
等式性质2
没有分母的项
要点归纳
趣味拓展
丢番图的墓志铭:
“坟中安葬着丢番图,多么令人惊讶,它忠实地记录了所经历的道路.上帝给予的童年占六分之一.又过十二分之一,两颊长胡.再过七分之一,点燃结婚的蜡烛.五年之后天赐贵子,可怜迟到的宁馨儿,享年仅及其父之半,便进入冰冷的墓.悲伤只有用数论的研究去弥补,又过四年,他也走完了人生的旅途.”
你知道丢番图去世时的年龄吗 请你列出方程
来算一算.
思考
https://www.21cnjy.com/help/help_extract.php
