12.2 三角形全等的判定(1)学案
文档属性
| 名称 | 12.2 三角形全等的判定(1)学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 75.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-07 22:26:56 | ||
图片预览

文档简介
12.2 三角形全等的判定(1)
【学习目标】
1、掌握三角形全等的判定(SSS),了解三角形的稳定性;
2、初步体会尺规作图;
3、掌握简单的证明格式.
【学习重点】
掌握三角形全等的“边边边”条件
【学习难点】
三角形全等条件的探索过程
【学习过程】
一、旧知回顾:
什么是全等形?什么是全等三角形?
叙述全等三角形的性质:
3、如图,△ABC≌△A′B′C′那么
相等的边是:
相等的角是:
二、新知探究
1、如果△ABC与△满足三条边分别相等和三个角分别相等,即
,, ,, ,,,你能判定ABC与
△全等吗?
2、按下列条件画△ABC与△,并判断你所画的两个三角形是否全等?
①两三角形满足一组对应边相等或一组对应角相等
△ABC与△中,=3cm △ABC与△中,=30°
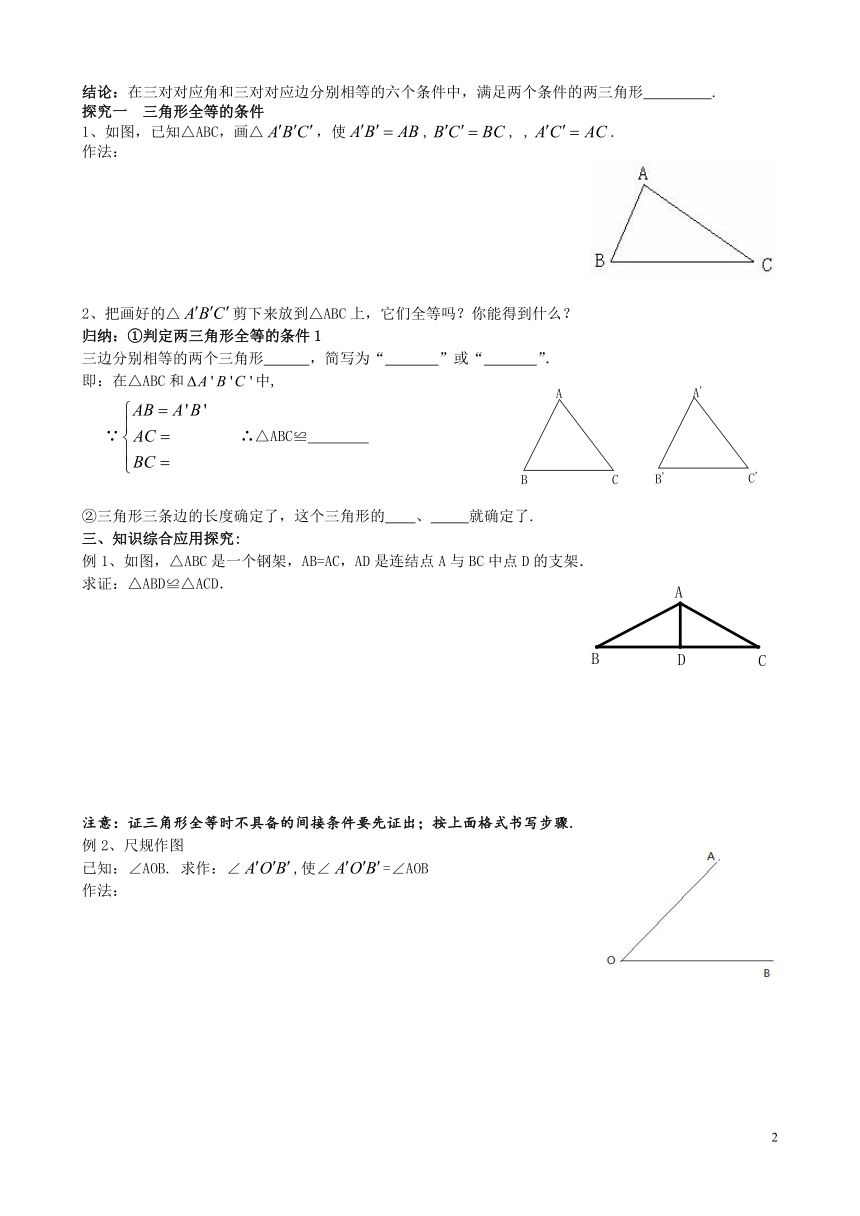
结论:在三对对应角和三对对应边分别相等的六个条件中,满足一个条件的两三角形 .
②两组对应边相等或两组对应角相等或一组对应边、对应角分别相等
△ABC与△中, △ABC与△中, △ABC与△中,
=3cm =30° =3cm
=2cm =45° =30°
结论:在三对对应角和三对对应边分别相等的六个条件中,满足两个条件的两三角形 .
探究一 三角形全等的条件
1、如图,已知△ABC,画△,使,, ,.
作法:
2、把画好的△剪下来放到△ABC上,它们全等吗?你能得到什么?
归纳:①判定两三角形全等的条件1
三边分别相等的两个三角形 ,简写为“ ”或“ ”.
即:在△ABC和中,
∵ ∴△ABC≌
②三角形三条边的长度确定了,这个三角形的 、 就确定了.
三、知识综合应用探究:
例1、如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.
求证:△ABD≌△ACD.
注意:证三角形全等时不具备的间接条件要先证出;按上面格式书写步骤.
例2、尺规作图
已知:∠AOB. 求作:∠,使∠=∠AOB
作法:
四、练习
1、如图,若D为BC中点,那么用“SSS”判定△ABD≌△ACD 需添加的一个条件是 ___________.
第1题 第2题 第3题 第4题 第5题
2、如图,已知OA = OB,AC = BC,∠1=30°,则∠ACB的度数是________.
3、如图,中,,,则由“”可以判定( )
A. B.C. D.以上答案都不对
4、如图,中,,,,则____,_____.
5、如图,,,,找出图中的全等三角形 ,并说明你的理由 .(任写一对)
6、如图,C是AB的中点,AD=CE,CD=BE,求证:△ACD≌△CBE.
7、工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,则过角尺顶点的射线OC就是∠AOB的平分线,为什么?
8、如图,AB=AE,AC=AD,BD=CE,求证:△ABC ≌ △ ADE。
9、已知:如图,AD=BC,AC=BD. 求证:∠OCD=∠ODC.
10、如图,AB = AD,DC = BC,∠B与∠D相等吗?为什么?
11、如图,在中,,分别为上的点,且,,.求证:.
12、如图,AD=CB,E、F是AC上两动点,且有DE=BF.
(1)若E、F运动至如图①所示的位置,且有AF=CE,求证:△ADE≌△CBF.
(2)若E、F运动至如图②所示的位置,仍有AF=CE,那么△ADE≌△CBF还成立吗?为什么?
(3)若E、F不重合,AD和CB平行吗?说明理由。
图① 图②
PAGE
1
【学习目标】
1、掌握三角形全等的判定(SSS),了解三角形的稳定性;
2、初步体会尺规作图;
3、掌握简单的证明格式.
【学习重点】
掌握三角形全等的“边边边”条件
【学习难点】
三角形全等条件的探索过程
【学习过程】
一、旧知回顾:
什么是全等形?什么是全等三角形?
叙述全等三角形的性质:
3、如图,△ABC≌△A′B′C′那么
相等的边是:
相等的角是:
二、新知探究
1、如果△ABC与△满足三条边分别相等和三个角分别相等,即
,, ,, ,,,你能判定ABC与
△全等吗?
2、按下列条件画△ABC与△,并判断你所画的两个三角形是否全等?
①两三角形满足一组对应边相等或一组对应角相等
△ABC与△中,=3cm △ABC与△中,=30°
结论:在三对对应角和三对对应边分别相等的六个条件中,满足一个条件的两三角形 .
②两组对应边相等或两组对应角相等或一组对应边、对应角分别相等
△ABC与△中, △ABC与△中, △ABC与△中,
=3cm =30° =3cm
=2cm =45° =30°
结论:在三对对应角和三对对应边分别相等的六个条件中,满足两个条件的两三角形 .
探究一 三角形全等的条件
1、如图,已知△ABC,画△,使,, ,.
作法:
2、把画好的△剪下来放到△ABC上,它们全等吗?你能得到什么?
归纳:①判定两三角形全等的条件1
三边分别相等的两个三角形 ,简写为“ ”或“ ”.
即:在△ABC和中,
∵ ∴△ABC≌
②三角形三条边的长度确定了,这个三角形的 、 就确定了.
三、知识综合应用探究:
例1、如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.
求证:△ABD≌△ACD.
注意:证三角形全等时不具备的间接条件要先证出;按上面格式书写步骤.
例2、尺规作图
已知:∠AOB. 求作:∠,使∠=∠AOB
作法:
四、练习
1、如图,若D为BC中点,那么用“SSS”判定△ABD≌△ACD 需添加的一个条件是 ___________.
第1题 第2题 第3题 第4题 第5题
2、如图,已知OA = OB,AC = BC,∠1=30°,则∠ACB的度数是________.
3、如图,中,,,则由“”可以判定( )
A. B.C. D.以上答案都不对
4、如图,中,,,,则____,_____.
5、如图,,,,找出图中的全等三角形 ,并说明你的理由 .(任写一对)
6、如图,C是AB的中点,AD=CE,CD=BE,求证:△ACD≌△CBE.
7、工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,则过角尺顶点的射线OC就是∠AOB的平分线,为什么?
8、如图,AB=AE,AC=AD,BD=CE,求证:△ABC ≌ △ ADE。
9、已知:如图,AD=BC,AC=BD. 求证:∠OCD=∠ODC.
10、如图,AB = AD,DC = BC,∠B与∠D相等吗?为什么?
11、如图,在中,,分别为上的点,且,,.求证:.
12、如图,AD=CB,E、F是AC上两动点,且有DE=BF.
(1)若E、F运动至如图①所示的位置,且有AF=CE,求证:△ADE≌△CBF.
(2)若E、F运动至如图②所示的位置,仍有AF=CE,那么△ADE≌△CBF还成立吗?为什么?
(3)若E、F不重合,AD和CB平行吗?说明理由。
图① 图②
PAGE
1
