第一章 预备知识 章末综合检测卷-北师大版(2019)必修第一册(Word版含答案)
文档属性
| 名称 | 第一章 预备知识 章末综合检测卷-北师大版(2019)必修第一册(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 105.8KB | ||
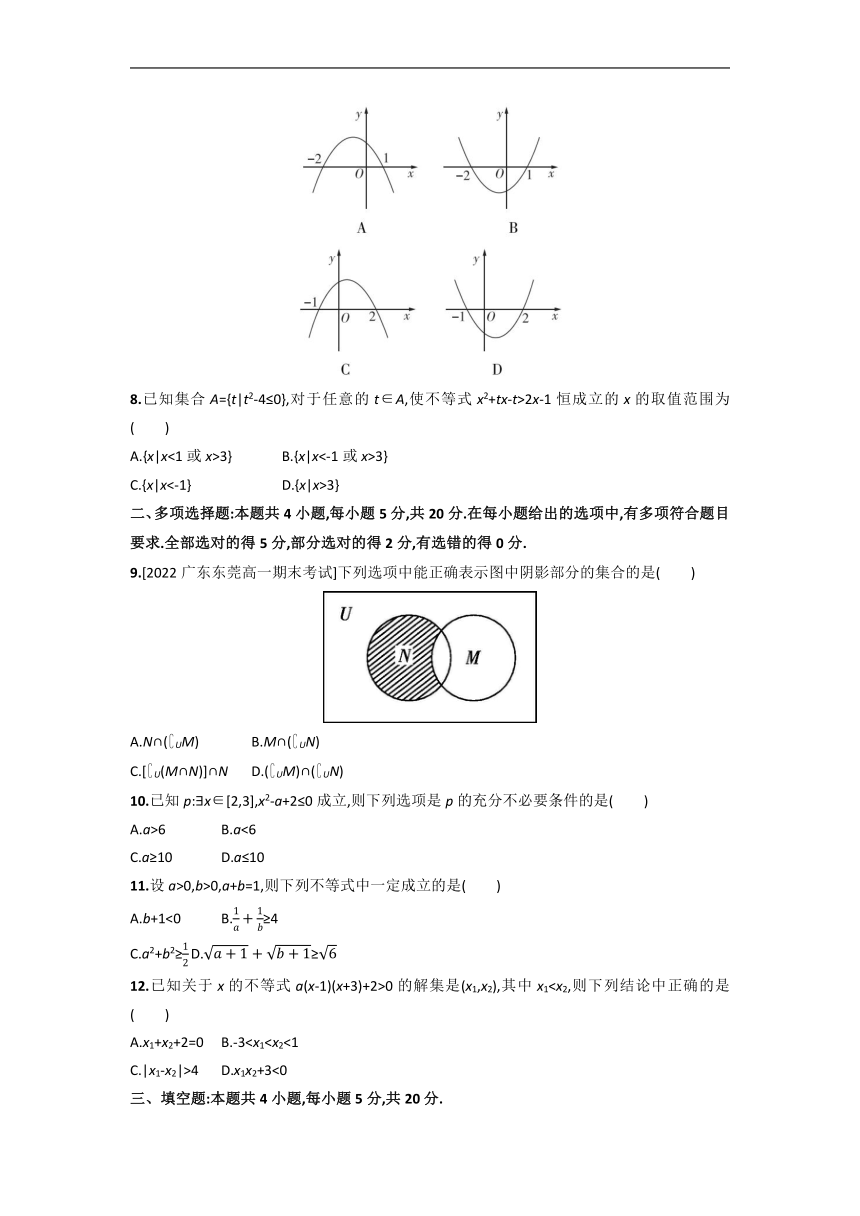
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-12 00:00:00 | ||
图片预览



文档简介
《第一章 预备知识》章末综合检测卷
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合A={0,1,2},B={1,m}.若B A,则实数m的值为( )
A.0 B.0或1
C.0或2 D.1或2
2.[2022江西赣州高一期末考试]已知集合A={x|x2-2x-3>0},集合B={x|y=},则( RA)∪B=( )
A.{x|-1≤x≤3} B.{x|x≥3}
C.{x|x≤-1} D.{x|x≥-1}
3.下列命题是真命题的是( )
A. n∈R,有n3≥n
B. n∈R, m∈R,有m·n=m
C. n∈R, m∈R,使m2D. n∈R,有n24.已知p:2x+3=x2,q:x=x2,则p是q的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
5.若<0,则下列不等式正确的是( )
A.|a|>|b| B.aC.a+b>ab D.a3>b3
6. 若关于x的不等式(1+k2)x≤k4+4的解集是M,则对任意常数k,总有( )
A.2∈M,0∈M
B.2 M,0 M
C.2∈M,0 M
D.2 M,0∈M
7.已知不等式ax2-x+c>0的解集为{x|-28.已知集合A={t|t2-4≤0},对于任意的t∈A,使不等式x2+tx-t>2x-1恒成立的x的取值范围为( )
A.{x|x<1或x>3} B.{x|x<-1或x>3}
C.{x|x<-1} D.{x|x>3}
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.[2022广东东莞高一期末考试]下列选项中能正确表示图中阴影部分的集合的是( )
A.N∩( UM) B.M∩( UN)
C.[ U(M∩N)]∩N D.( UM)∩( UN)
10.已知p: x∈[2,3],x2-a+2≤0成立,则下列选项是p的充分不必要条件的是( )
A.a>6 B.a<6
C.a≥10 D.a≤10
11.设a>0,b>0,a+b=1,则下列不等式中一定成立的是( )
A.b+1<0 B.≥4
C.a2+b2≥ D.≥
12.已知关于x的不等式a(x-1)(x+3)+2>0的解集是(x1,x2),其中x1A.x1+x2+2=0 B.-3C.|x1-x2|>4 D.x1x2+3<0
三、填空题:本题共4小题,每小题5分,共20分.
13.已知p: 4x-m<0,q:1≤3-x≤4,若p是q的必要条件,则实数m的取值范围为 .
14.已知命题“存在x∈R,使ax2-x+2≤0”是假命题,则实数a的取值范围是 .
15.已知关于x的不等式ax0的解集为 .(本题第一空2分,第二空3分.)
16.已知x>0,y>0且x+y=2,则的最小值为 .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)在①B ( RA),②( RA)∪B=R,③A∩B=B这三个条件中任选一个,补充在下面问题中,并解答.
问题:已知集合A={x|x2-5x+4≤0},B={x|a+1注:如果选择多个条件分别解答,按第一个解答计分.
18.(12分)已知不等式|2x+3|<1的解集为集合A,关于x的不等式x2-(2a+2)x+a2+2a≤0的解集为集合B.
(1)当a=-2时,求集合B;
(2)设p:x∈A,q:x∈B,若q是p的必要不充分条件,求实数a的取值范围.
19.(12分)已知关于x的不等式kx2-2x+6k<0(k≠0).
(1)若不等式的解集是{x|x<-3或x>-2},求实数k的值;
(2)若不等式的解集是R,求实数k的取值范围;
(3)若不等式的解集为 ,求实数k的取值范围.
20.(12分)已知关于x的不等式ax2-3x+2>0的解集为{x|x<1或x>b}.
(1)求实数a,b的值;
(2)当x>0,y>0,且=1时,2x+y≥k2+k+2恒成立,求实数k的取值范围.
21.(12分)[2022江苏苏州高一期末考试]设函数y=x2-4mx+m的图象与平面直角坐标系中的x轴交于不同的两点A(x1,0),B(x2,0).
(1)当m=1时,求的值;
(2)若x1>0,x2>0,求实数m的取值范围,及x1+4x2的最小值.
22.(12分)汽车智能辅助驾驶已开始得到应用,其自动刹车的工作原理是用雷达测出车辆与前方障碍物之间的距离(并结合车速转化为所需时间),当此距离等于报警距离时就开启报警提醒,等于危险距离时就自动刹车.某种算法将报警时间分为4段(如图所示),分别为准备时间t0、人的反应时间t1、系统反应时间t2、制动时间t3,相应的距离分别为d0,d1,d2,d3,当车速为v(单位:m/s),且0≤v≤33.3时,通过大数据统计分析得到下表(其中系数k随地面湿滑程度等路面情况而变化,且0.5≤k≤0.9).
阶段 准备 人的反应 系统反应 制动
时间 t0 t1=0.8 s t2=0.2 s t3
距离 d0=20 m d1 d2 d3= m
(1)请写出报警距离d(单位:m)与车速v(单位:m/s)之间的表达式;若汽车达到报警距离时人和系统均不采取任何制动措施,仍以速度v行驶,求当k=0.9时,汽车撞上固定障碍物的最短时间;
(2)若要求汽车不论在何种路面情况下行驶,报警距离均小于80 m,则汽车的行驶速度应限制在多少以下
参考答案
一、单项选择题
1.C 2.D 3.B 4.D 5.D 6.A 7.C 8.B
二、多项选择题
9.AC 10.AC 11.BC 12.ACD
三、填空题
13.(8,+∞)
14.(,+∞)
15.-2 {x|-116. 3
四、解答题
17.方案一:选条件①.
由题意,得A={x|1≤x≤4},(1分)
所以 RA ={x|x<1或x>4}.(3分)
当B= ,即a+1≥2a-1,即a≤2时,符合题意;(5分)
当B≠ 时,由B ( RA),
得或,解得a≥3.(9分)
综上,存在实数a,使得B ( RA),且实数a的取值范围为(-∞,2]∪[3,+∞).(10分)
方案二:选条件②.
由题意,得A={x|1≤x≤4},(1分)
所以 RA ={x|x<1或x>4}.(3分)
由( RA)∪B=R,得,无解.(9分)
故不存在实数a,使得( RA)∪B=R.(10分)
方案三:选条件③.
由题意,得A={x|1≤x≤4}.(1分)
因为A∩B=B,所以B A.(3分)
当B= ,即a+1≥2a-1,即a≤2时,符合题意;(5分)
当B≠ 时,由B A,得,解得2综上,存在实数a,使得A∩B=B,且实数a的取值范围为(-∞,].(10分)
18.(1)由x2-(2a+2)x+a2+2a=(x-a)(x-a-2)≤0,得a≤x≤a+2,
故B={x|a≤x≤a+2}.(3分)
所以当a=-2时,B={x|-2≤x≤0}.(5分)
(2)由(1),得B={x|a≤x≤a+2}.
由|2x+3|<1,得-2故A={x|-2因为q是p的必要不充分条件,所以A B,(9分)
故,解得-3≤a≤-2.
所以实数a的取值范围是[-3,-2].(12分)
19.(1)由题可知-3和-2是关于x的方程kx2-2x+6k=0的两个实数根,且k<0,
所以(-3)+(-2)=,所以k=-.(4分)
(2)由题可得,解得k<-,
所以实数k的取值范围是(-∞,-).(8分)
(3)由题可得,解得k≥,
所以实数k的取值范围是[,+∞).(12分)
20.(1)因为不等式ax2-3x+2>0的解集为{x|x<1或x>b},
所以1和b是关于x的方程ax2-3x+2=0的两个实数根,且a>0,(2分)
所以,解得.(5分)
(2)由(1)知,于是有=1,
故2x+y=(2x+y)()=4+≥8,
当且仅当时等号成立,(9分)
依题意有2x+y的最小值大于等于k2+k+2,即8≥k2+k+2,解得-3≤k≤2,
所以实数k的取值范围为[-3,2].(12分)
21.(1)当m=1时,函数y=x2-4x+1,由题意,得关于x的方程x2-4x+1=0有两个实数根x1,x2,所以,
故=-4.(4分)
(2)由题意,知关于x的方程x2-4mx+m=0有两个不相等的正实数根,
所以,即,解得m>.所以实数m的取值范围为(,+∞).(7分)
又x1+x2=4x1x2,x1>0,x2>0,所以=4,
所以x1+4x2=(x1+4x2)()=(1+4+)≥(5+2)=,当且仅当,即x1=,x2=时取得“=”,此时实数m=符合条件,故x1+4x2取得最小值.(12分)
22.(1)根据题意,得d=d0+d1+d2+d3=20+0.8v+0.2v+=20+v+(0≤v≤33.3).(2分)
当k=0.9时,所求函数关系式为d=20+v+,(3分)
t=+1≥2+1=,当且仅当,即v=6时等号成立.
所以当k=0.9时,汽车撞上固定障碍物的最短时间是 s.(6分)
(2)根据题意,得对任意的k∈[0.5,0.9],d<80恒成立,
即对任意的k∈[0.5,0.9],20+v+<80恒成立.(8分)
易知当v=0时,满足题意;当0由k∈[0.5,0.9],得∈[,],
所以,即v2+10v-600<0,
解得-30综上,0≤v<20.
所以汽车的行驶速度应限制在20 m/s以下.(12分)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合A={0,1,2},B={1,m}.若B A,则实数m的值为( )
A.0 B.0或1
C.0或2 D.1或2
2.[2022江西赣州高一期末考试]已知集合A={x|x2-2x-3>0},集合B={x|y=},则( RA)∪B=( )
A.{x|-1≤x≤3} B.{x|x≥3}
C.{x|x≤-1} D.{x|x≥-1}
3.下列命题是真命题的是( )
A. n∈R,有n3≥n
B. n∈R, m∈R,有m·n=m
C. n∈R, m∈R,使m2
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
5.若<0,则下列不等式正确的是( )
A.|a|>|b| B.a
6. 若关于x的不等式(1+k2)x≤k4+4的解集是M,则对任意常数k,总有( )
A.2∈M,0∈M
B.2 M,0 M
C.2∈M,0 M
D.2 M,0∈M
7.已知不等式ax2-x+c>0的解集为{x|-2
A.{x|x<1或x>3} B.{x|x<-1或x>3}
C.{x|x<-1} D.{x|x>3}
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.[2022广东东莞高一期末考试]下列选项中能正确表示图中阴影部分的集合的是( )
A.N∩( UM) B.M∩( UN)
C.[ U(M∩N)]∩N D.( UM)∩( UN)
10.已知p: x∈[2,3],x2-a+2≤0成立,则下列选项是p的充分不必要条件的是( )
A.a>6 B.a<6
C.a≥10 D.a≤10
11.设a>0,b>0,a+b=1,则下列不等式中一定成立的是( )
A.b+1<0 B.≥4
C.a2+b2≥ D.≥
12.已知关于x的不等式a(x-1)(x+3)+2>0的解集是(x1,x2),其中x1
三、填空题:本题共4小题,每小题5分,共20分.
13.已知p: 4x-m<0,q:1≤3-x≤4,若p是q的必要条件,则实数m的取值范围为 .
14.已知命题“存在x∈R,使ax2-x+2≤0”是假命题,则实数a的取值范围是 .
15.已知关于x的不等式ax
16.已知x>0,y>0且x+y=2,则的最小值为 .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)在①B ( RA),②( RA)∪B=R,③A∩B=B这三个条件中任选一个,补充在下面问题中,并解答.
问题:已知集合A={x|x2-5x+4≤0},B={x|a+1
18.(12分)已知不等式|2x+3|<1的解集为集合A,关于x的不等式x2-(2a+2)x+a2+2a≤0的解集为集合B.
(1)当a=-2时,求集合B;
(2)设p:x∈A,q:x∈B,若q是p的必要不充分条件,求实数a的取值范围.
19.(12分)已知关于x的不等式kx2-2x+6k<0(k≠0).
(1)若不等式的解集是{x|x<-3或x>-2},求实数k的值;
(2)若不等式的解集是R,求实数k的取值范围;
(3)若不等式的解集为 ,求实数k的取值范围.
20.(12分)已知关于x的不等式ax2-3x+2>0的解集为{x|x<1或x>b}.
(1)求实数a,b的值;
(2)当x>0,y>0,且=1时,2x+y≥k2+k+2恒成立,求实数k的取值范围.
21.(12分)[2022江苏苏州高一期末考试]设函数y=x2-4mx+m的图象与平面直角坐标系中的x轴交于不同的两点A(x1,0),B(x2,0).
(1)当m=1时,求的值;
(2)若x1>0,x2>0,求实数m的取值范围,及x1+4x2的最小值.
22.(12分)汽车智能辅助驾驶已开始得到应用,其自动刹车的工作原理是用雷达测出车辆与前方障碍物之间的距离(并结合车速转化为所需时间),当此距离等于报警距离时就开启报警提醒,等于危险距离时就自动刹车.某种算法将报警时间分为4段(如图所示),分别为准备时间t0、人的反应时间t1、系统反应时间t2、制动时间t3,相应的距离分别为d0,d1,d2,d3,当车速为v(单位:m/s),且0≤v≤33.3时,通过大数据统计分析得到下表(其中系数k随地面湿滑程度等路面情况而变化,且0.5≤k≤0.9).
阶段 准备 人的反应 系统反应 制动
时间 t0 t1=0.8 s t2=0.2 s t3
距离 d0=20 m d1 d2 d3= m
(1)请写出报警距离d(单位:m)与车速v(单位:m/s)之间的表达式;若汽车达到报警距离时人和系统均不采取任何制动措施,仍以速度v行驶,求当k=0.9时,汽车撞上固定障碍物的最短时间;
(2)若要求汽车不论在何种路面情况下行驶,报警距离均小于80 m,则汽车的行驶速度应限制在多少以下
参考答案
一、单项选择题
1.C 2.D 3.B 4.D 5.D 6.A 7.C 8.B
二、多项选择题
9.AC 10.AC 11.BC 12.ACD
三、填空题
13.(8,+∞)
14.(,+∞)
15.-2 {x|-1
四、解答题
17.方案一:选条件①.
由题意,得A={x|1≤x≤4},(1分)
所以 RA ={x|x<1或x>4}.(3分)
当B= ,即a+1≥2a-1,即a≤2时,符合题意;(5分)
当B≠ 时,由B ( RA),
得或,解得a≥3.(9分)
综上,存在实数a,使得B ( RA),且实数a的取值范围为(-∞,2]∪[3,+∞).(10分)
方案二:选条件②.
由题意,得A={x|1≤x≤4},(1分)
所以 RA ={x|x<1或x>4}.(3分)
由( RA)∪B=R,得,无解.(9分)
故不存在实数a,使得( RA)∪B=R.(10分)
方案三:选条件③.
由题意,得A={x|1≤x≤4}.(1分)
因为A∩B=B,所以B A.(3分)
当B= ,即a+1≥2a-1,即a≤2时,符合题意;(5分)
当B≠ 时,由B A,得,解得2
18.(1)由x2-(2a+2)x+a2+2a=(x-a)(x-a-2)≤0,得a≤x≤a+2,
故B={x|a≤x≤a+2}.(3分)
所以当a=-2时,B={x|-2≤x≤0}.(5分)
(2)由(1),得B={x|a≤x≤a+2}.
由|2x+3|<1,得-2
故,解得-3≤a≤-2.
所以实数a的取值范围是[-3,-2].(12分)
19.(1)由题可知-3和-2是关于x的方程kx2-2x+6k=0的两个实数根,且k<0,
所以(-3)+(-2)=,所以k=-.(4分)
(2)由题可得,解得k<-,
所以实数k的取值范围是(-∞,-).(8分)
(3)由题可得,解得k≥,
所以实数k的取值范围是[,+∞).(12分)
20.(1)因为不等式ax2-3x+2>0的解集为{x|x<1或x>b},
所以1和b是关于x的方程ax2-3x+2=0的两个实数根,且a>0,(2分)
所以,解得.(5分)
(2)由(1)知,于是有=1,
故2x+y=(2x+y)()=4+≥8,
当且仅当时等号成立,(9分)
依题意有2x+y的最小值大于等于k2+k+2,即8≥k2+k+2,解得-3≤k≤2,
所以实数k的取值范围为[-3,2].(12分)
21.(1)当m=1时,函数y=x2-4x+1,由题意,得关于x的方程x2-4x+1=0有两个实数根x1,x2,所以,
故=-4.(4分)
(2)由题意,知关于x的方程x2-4mx+m=0有两个不相等的正实数根,
所以,即,解得m>.所以实数m的取值范围为(,+∞).(7分)
又x1+x2=4x1x2,x1>0,x2>0,所以=4,
所以x1+4x2=(x1+4x2)()=(1+4+)≥(5+2)=,当且仅当,即x1=,x2=时取得“=”,此时实数m=符合条件,故x1+4x2取得最小值.(12分)
22.(1)根据题意,得d=d0+d1+d2+d3=20+0.8v+0.2v+=20+v+(0≤v≤33.3).(2分)
当k=0.9时,所求函数关系式为d=20+v+,(3分)
t=+1≥2+1=,当且仅当,即v=6时等号成立.
所以当k=0.9时,汽车撞上固定障碍物的最短时间是 s.(6分)
(2)根据题意,得对任意的k∈[0.5,0.9],d<80恒成立,
即对任意的k∈[0.5,0.9],20+v+<80恒成立.(8分)
易知当v=0时,满足题意;当0
所以,即v2+10v-600<0,
解得-30
所以汽车的行驶速度应限制在20 m/s以下.(12分)
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
