北师大版数学八年级上册第1章勾股定理 单元复习课课件(共21张PPT)
文档属性
| 名称 | 北师大版数学八年级上册第1章勾股定理 单元复习课课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 263.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-13 18:07:17 | ||
图片预览








文档简介
(共21张PPT)
第一章 勾股定理
单元复习课
本章知识梳理
目录
01
课标要求
02
知识导航
课标要求
探索勾股定理及其逆定理,并能运用它们解决一些简单的
实际问题.
知识导航
勾股定理 定义:直角三角形两直角边的平方和等于斜边的平方. 如果用a,b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2
直角三角形的判定条件(勾股定理的逆定理):如果三角形的三边长a,b,c满足a2+b2=c2. 那么这个三角形是直角三角形
勾股数:满足a2+b2=c2的三个正整数,称为勾股数
应用 求立体图形表面上两点间的最短距离
根据已知条件,利用勾股定理求相应的未知数
1. 下列由线段a,b,c组成的三角形是直角三角形的是( )
A. a=1,b=2,c=3
B. a=4,b=5,c=6
C. a=9,b=12,c=15
D. a=13,b=14,c=15
专题1 勾股定理及直角三角形的判定
C
2. 《赵爽弦图》巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲. 如图Z1-1所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形. 设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为( )
A. 9 B. 6 C. 4 D. 3
D
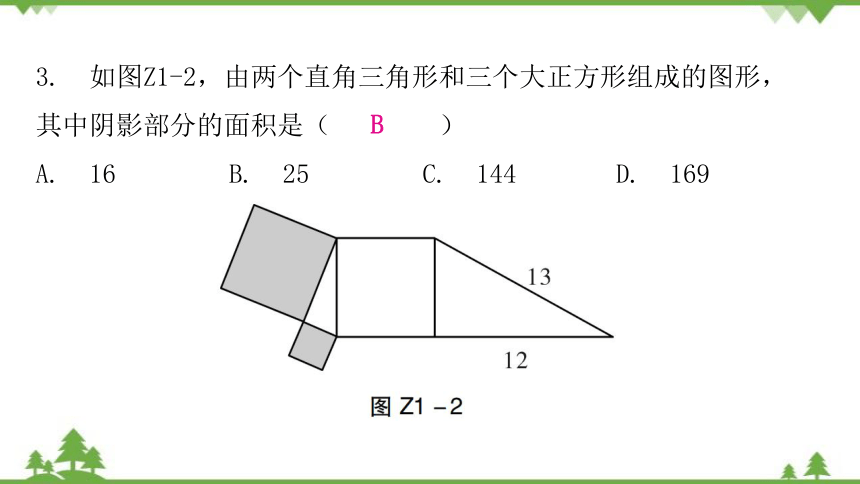
3. 如图Z1-2,由两个直角三角形和三个大正方形组成的图形,其中阴影部分的面积是( )
A. 16 B. 25 C. 144 D. 169
B
4. 在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A
5. 在△ABC中,∠C=90°,c2=2b2,则两直角边a,b的关系是( )
A. a<b
B. a>b
C. a=b
D. 以上三种情况都有可能
C
6. 如图Z1-3所示是由三个直角三角形组成的梯形,根据图形,写出一个正确的等式:____________.
c2=a2+b2
7. 已知a,b,c是一组勾股数,把这三个数分别扩大2倍,所得的三个数还是勾股数吗?扩大k倍呢?验证你的结论.
解:因为2是正整数,a,b,c是一组勾股数,
所以2a,2b,2c都是正整数.
因为a2+b2=c2,所以(2a)2+(2b)2=(2c)2.
所以2a,2b,2c是一组勾股数.
因为a,b,c是一组勾股数,且k是正整数,
所以ak,bk,ck是三个正整数.
因为a2+b2=c2,
所以(ak)2+(bk)2=a2k2+b2k2=(a2+b2)k2=c2k2=(ck)2.
所以ak,bk,ck是一组勾股数.
8. 已知如图Z1-4,在△ABC中,BC=6,AC=8,DE⊥AB,DE=7,△ABE的面积为35,求△ACB的面积.
解:因为DE=7,△ABE的面积为35,
所以 ×AB×7=35.
所以AB=10.
又因为BC=6,AC=8,
所以AC2+BC2=100=AB2.
所以∠C=90°.
所以S△ACB= ×6×8=24.
1. 放学以后,小红和小颖从学校分手,分别沿东南方向和西南方向回家,若小红和小颖行走的速度都是40 米/分,小红用15分钟到家,小颖用20分钟到家,则小红和小颖家的直线距离为( )
A. 600米 B. 800米
C. 1 000米 D. 不能确定
专题2 勾股定理的应用
C
2. 如图Z1-5,圆柱的底面半径是4,高是5,一只在A点的蚂蚁想吃到B点的食物,需要爬行的最短路径是(π取3)( )
A. 9
B. 13
C. 14
D. 25
B
3. 如图Z1-6所示是一扇高为2 m,宽为1.5 m的门框.李师傅有3块薄木板,尺寸如下:①号木板长3 m,宽2.7 m;②号木板长2.8 m,宽2.8 m;③号木板长4 m,宽2.4 m. 可以从这扇门通过的木板是( )
A. ①号 B. ②号
C. ③号 D. 均不能通过
C
4. 一个矩形的抽斗长为12 cm,宽为5 cm,在抽斗内部放一根铁条,那么铁条最长可以是_________ cm.
5. 如图Z1-7,一棵高为16 m的大树被台风刮断,若树在离地面6 m处折断,树顶端刚好落在地面上,则此处离树底部有_________ m.
13
8
6. 无盖圆柱形杯子的展开图如图Z1-8. 将一根长为20 cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有_________ cm.
5
7. 如图Z1-9,长方形ABCD是一个花园,其中AB=15 m,BC=8 m,在花园内修一条长13 m的笔直小路EF,小路出口一端E选在AD边上距D点3 m处,另一端出口F应选在AB边上距B点几米处?
解:由题意知EF=13 m,EA=8-3=5(m).
在Rt△EAF中,由勾股定理,得AF2=EF2-EA2,
即AF2=132-52=144.
所以AF=12(m).
所以FB=15-12=3(m).
答:另一端出口F应选在AB边上距B点3 m处.
8. 如图Z1-10,“远航”号、“海天”号轮船同时离开港口P,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开
港口一个半小时后相距30海里.
如果知道“远航”号沿北偏东60°
方向航行,那么“海天”号沿哪
个方向航行呢?
解:根据题意,得PQ=16×1.5=24(海里),
PR=12×1.5=18(海里),QR=30(海里).
因为242+182=302,即PQ2+PR2=QR2,
所以△QPR是直角三角形. 所以∠QPR=90°.
由“远航号”沿北偏东60°方向航行可知,∠QPS=60°,则∠SPR=30°,即“海天”号沿北偏西30°方向航行.
谢 谢
第一章 勾股定理
单元复习课
本章知识梳理
目录
01
课标要求
02
知识导航
课标要求
探索勾股定理及其逆定理,并能运用它们解决一些简单的
实际问题.
知识导航
勾股定理 定义:直角三角形两直角边的平方和等于斜边的平方. 如果用a,b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2
直角三角形的判定条件(勾股定理的逆定理):如果三角形的三边长a,b,c满足a2+b2=c2. 那么这个三角形是直角三角形
勾股数:满足a2+b2=c2的三个正整数,称为勾股数
应用 求立体图形表面上两点间的最短距离
根据已知条件,利用勾股定理求相应的未知数
1. 下列由线段a,b,c组成的三角形是直角三角形的是( )
A. a=1,b=2,c=3
B. a=4,b=5,c=6
C. a=9,b=12,c=15
D. a=13,b=14,c=15
专题1 勾股定理及直角三角形的判定
C
2. 《赵爽弦图》巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲. 如图Z1-1所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形. 设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为( )
A. 9 B. 6 C. 4 D. 3
D
3. 如图Z1-2,由两个直角三角形和三个大正方形组成的图形,其中阴影部分的面积是( )
A. 16 B. 25 C. 144 D. 169
B
4. 在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A
5. 在△ABC中,∠C=90°,c2=2b2,则两直角边a,b的关系是( )
A. a<b
B. a>b
C. a=b
D. 以上三种情况都有可能
C
6. 如图Z1-3所示是由三个直角三角形组成的梯形,根据图形,写出一个正确的等式:____________.
c2=a2+b2
7. 已知a,b,c是一组勾股数,把这三个数分别扩大2倍,所得的三个数还是勾股数吗?扩大k倍呢?验证你的结论.
解:因为2是正整数,a,b,c是一组勾股数,
所以2a,2b,2c都是正整数.
因为a2+b2=c2,所以(2a)2+(2b)2=(2c)2.
所以2a,2b,2c是一组勾股数.
因为a,b,c是一组勾股数,且k是正整数,
所以ak,bk,ck是三个正整数.
因为a2+b2=c2,
所以(ak)2+(bk)2=a2k2+b2k2=(a2+b2)k2=c2k2=(ck)2.
所以ak,bk,ck是一组勾股数.
8. 已知如图Z1-4,在△ABC中,BC=6,AC=8,DE⊥AB,DE=7,△ABE的面积为35,求△ACB的面积.
解:因为DE=7,△ABE的面积为35,
所以 ×AB×7=35.
所以AB=10.
又因为BC=6,AC=8,
所以AC2+BC2=100=AB2.
所以∠C=90°.
所以S△ACB= ×6×8=24.
1. 放学以后,小红和小颖从学校分手,分别沿东南方向和西南方向回家,若小红和小颖行走的速度都是40 米/分,小红用15分钟到家,小颖用20分钟到家,则小红和小颖家的直线距离为( )
A. 600米 B. 800米
C. 1 000米 D. 不能确定
专题2 勾股定理的应用
C
2. 如图Z1-5,圆柱的底面半径是4,高是5,一只在A点的蚂蚁想吃到B点的食物,需要爬行的最短路径是(π取3)( )
A. 9
B. 13
C. 14
D. 25
B
3. 如图Z1-6所示是一扇高为2 m,宽为1.5 m的门框.李师傅有3块薄木板,尺寸如下:①号木板长3 m,宽2.7 m;②号木板长2.8 m,宽2.8 m;③号木板长4 m,宽2.4 m. 可以从这扇门通过的木板是( )
A. ①号 B. ②号
C. ③号 D. 均不能通过
C
4. 一个矩形的抽斗长为12 cm,宽为5 cm,在抽斗内部放一根铁条,那么铁条最长可以是_________ cm.
5. 如图Z1-7,一棵高为16 m的大树被台风刮断,若树在离地面6 m处折断,树顶端刚好落在地面上,则此处离树底部有_________ m.
13
8
6. 无盖圆柱形杯子的展开图如图Z1-8. 将一根长为20 cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有_________ cm.
5
7. 如图Z1-9,长方形ABCD是一个花园,其中AB=15 m,BC=8 m,在花园内修一条长13 m的笔直小路EF,小路出口一端E选在AD边上距D点3 m处,另一端出口F应选在AB边上距B点几米处?
解:由题意知EF=13 m,EA=8-3=5(m).
在Rt△EAF中,由勾股定理,得AF2=EF2-EA2,
即AF2=132-52=144.
所以AF=12(m).
所以FB=15-12=3(m).
答:另一端出口F应选在AB边上距B点3 m处.
8. 如图Z1-10,“远航”号、“海天”号轮船同时离开港口P,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开
港口一个半小时后相距30海里.
如果知道“远航”号沿北偏东60°
方向航行,那么“海天”号沿哪
个方向航行呢?
解:根据题意,得PQ=16×1.5=24(海里),
PR=12×1.5=18(海里),QR=30(海里).
因为242+182=302,即PQ2+PR2=QR2,
所以△QPR是直角三角形. 所以∠QPR=90°.
由“远航号”沿北偏东60°方向航行可知,∠QPS=60°,则∠SPR=30°,即“海天”号沿北偏西30°方向航行.
谢 谢
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
