冀教版数学七年级上册 5.4第2课时 列一元一次方程解决相遇问题、工程问题 课件(共20张PPT)
文档属性
| 名称 | 冀教版数学七年级上册 5.4第2课时 列一元一次方程解决相遇问题、工程问题 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-13 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
5.4 一元一次方程的应用
第五章 一元一次方程
第2课时 列一元一次方程解决相遇问题、工程问题
学习目标
1.掌握相遇问题、工程问题中的基本等量关系;(重点)
2.学会利用线段图分析相遇问题及工程问题,分清有关数量关系,找出主要等量关系,准确列出方程;(难点)
3.进一步掌握用一元一次方程解决实际问题的基本过程.(重点)
导入新课
情境引入
你知道它蕴含的是我们数学中的什么问题吗?
讲授新课
相遇问题
一
合作探究
甲、乙两地间的路程为375km.一辆轿车和一辆公共汽车分别从甲、乙两地同时出发沿公路相向而行.轿车的平均速度为90km/h,公共汽车的平均速度为60km/h.它们出发后多少小时在途中相遇?
问题1:找出本题中的等量关系.
轿车行驶的路程+公共汽车行驶的路程=甲乙两地间的路程.
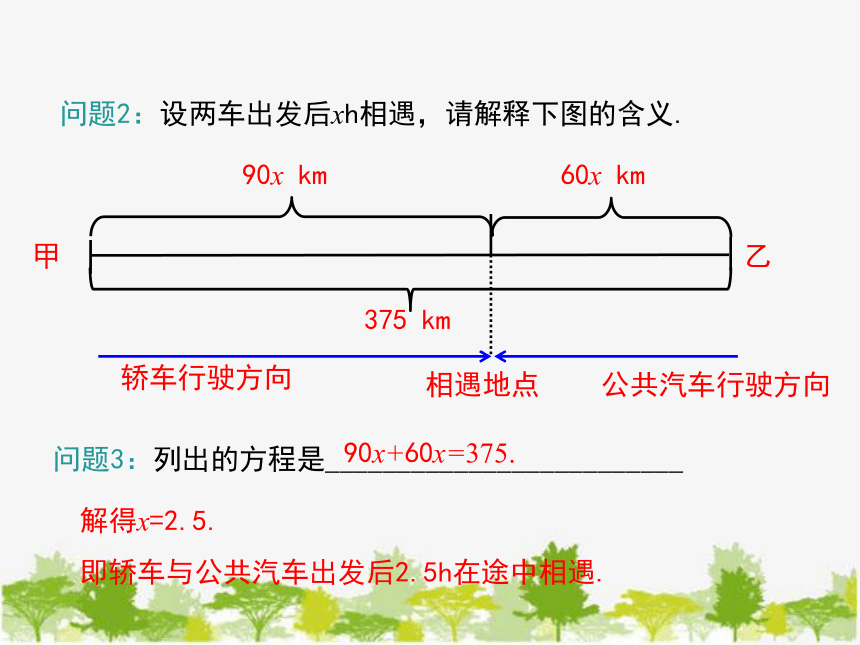
问题2:设两车出发后xh相遇,请解释下图的含义.
375 km
甲
乙
90x km
60x km
轿车行驶方向
公共汽车行驶方向
相遇地点
问题3:列出的方程是_________________________
90x+60x=375.
解得x=2.5.
即轿车与公共汽车出发后2.5h在途中相遇.
例1 小明与小红的家相距20km,小明从家里出发骑自行车去小红家,两人商定小红到时候从家里出发骑自行车去接小明. 已知小明骑车的速度为13 km/h,小红骑车的速度是12 km/h.
(1)如果两人同时出发,那么他们经过多少小时相遇?
分析:由于小明与小红都从家里出发,相向而行,所以相遇时,他们走的路程的和等于两家之间的距离.即
小明走的路程+小红走的路程=两家之间的距离(20km).
典例精析
解:(1)设小明与小红骑车走了x h后相遇,
则根据等量关系,得
13x + 12x = 20 .
解得 x = 0.8 .
答:经过0.8 h他们两人相遇.
小明走的路程
小红走的路程
(2)如果小明先走30min,那么小红骑车要走多少小时才能与小明相遇?
小明先走的路程
小红出发后小明走的路程
小红走的路程
解:(2)设小红骑车走了t h后与小明相遇,
则根据等量关系,得
13(0.5 + t )+12t = 20 .
解得 t = 0.54 .
答:小红骑车走0.54h后与小明相遇.
路程=速度×时间
甲走的路程+乙走的路程=甲、乙之间的距离
相遇问题
总结归纳
注意相向而行的始发时间和地点
甲、乙两站相距480千米,一列慢车从甲站开出,每小时行90千米,一列快车从乙站开出,每小时行140千米.慢车先开出1小时,快车再开,两车相向而行.问快车开出多少小时后两车相遇?
练一练
解:设快车开出x小时后两车相遇.
依题意,得: 90×1+90x+140x=480.
解方程,得:
答:快车开出 小时后两车相遇.
工程问题
二
典例精析
例2 一项工作,小李单独做需要6h完成,小王单独做需要9h完成.如果小李先做2h后,再由两人合做,那么还需几小时才能完成 ?
分析:如果设还需两人合做xh才能完成,那么有下面分析图.
小李单独做2h完成的工作量
小王、小李合做xh完成的工作量
总工作量
解:设两人合做x小时才能完成.依题意,得
解得
答:两人合做 小时才能完成这项工作.
生产的这批螺钉、螺母要打包,由一个人做要40 h 完成.现计划由一部分人先做4 h,然后增加 2人与他们一起做8 h,完成这项工作. 假设这些人的工作效率相同,具体应该安排多少人工作?
列表分析:
人均效率 人数 时间 工作量
前一部分工作 x 4
后一部分工作 x+2 8
×
=
×
×
×
=
工作量之和等于总工作量1
试一试
解:设先安排 x 人做4 h,根据题意得等量关系:
可列方程
解方程,得
4x+8(x+2)=40,
4x+8x+16=40,
12x=24,
x=2.
答:应先安排 2人做4 小时.
前部分工作总量+后部分工作总量=总工作量1
解决工程问题的思路:
1.三个基本量:
工程问题中的三个基本量:工作总量、工作效率、工作时间,
它们之间的关系是:工作总量=工作效率×工作时间.
若把工作量看作1,则工作效率=
2.相等关系:
(1)按工作时间,各时间段的工作量之和=完成的工作量.
(2)按工作者,若一项工作有甲、乙两人参与,则甲的工作量
+乙的工作量=完成的工作量.
要点归纳
当堂练习
1.甲、乙两人骑摩托车同时从相距170千米的A,B两地相向而行,2小时相遇,如果甲比乙每小时多行5千米,则乙每小时行( )
A.30千米 B.40千米 C.50千米 D.45千米
2.甲、乙两人在400米的环形跑道上练习长跑,他们同时同地反向而跑,甲的速度是6米/秒,乙的速度是4米/秒,则他们首次相遇时,两人都跑了( )
A.40秒 B.50秒 C.60秒 D.70秒
B
A
3.一项工作,甲独做需18天,乙独做需24天,如果两人合做8天后,余下的工作再由甲独做x天完成,
那么所列方程为____________.
课堂小结
列一元一次方程解决相遇问题、工程问题
相遇问题
工程问题
路程=速度×时间
甲走的路程+乙走的路程=甲、乙之间的距离
甲的工作量+乙的工作量=完成的工作量
各时间段的工作量之和=完成的工作量
工作总量=工作效率×工作时间
5.4 一元一次方程的应用
第五章 一元一次方程
第2课时 列一元一次方程解决相遇问题、工程问题
学习目标
1.掌握相遇问题、工程问题中的基本等量关系;(重点)
2.学会利用线段图分析相遇问题及工程问题,分清有关数量关系,找出主要等量关系,准确列出方程;(难点)
3.进一步掌握用一元一次方程解决实际问题的基本过程.(重点)
导入新课
情境引入
你知道它蕴含的是我们数学中的什么问题吗?
讲授新课
相遇问题
一
合作探究
甲、乙两地间的路程为375km.一辆轿车和一辆公共汽车分别从甲、乙两地同时出发沿公路相向而行.轿车的平均速度为90km/h,公共汽车的平均速度为60km/h.它们出发后多少小时在途中相遇?
问题1:找出本题中的等量关系.
轿车行驶的路程+公共汽车行驶的路程=甲乙两地间的路程.
问题2:设两车出发后xh相遇,请解释下图的含义.
375 km
甲
乙
90x km
60x km
轿车行驶方向
公共汽车行驶方向
相遇地点
问题3:列出的方程是_________________________
90x+60x=375.
解得x=2.5.
即轿车与公共汽车出发后2.5h在途中相遇.
例1 小明与小红的家相距20km,小明从家里出发骑自行车去小红家,两人商定小红到时候从家里出发骑自行车去接小明. 已知小明骑车的速度为13 km/h,小红骑车的速度是12 km/h.
(1)如果两人同时出发,那么他们经过多少小时相遇?
分析:由于小明与小红都从家里出发,相向而行,所以相遇时,他们走的路程的和等于两家之间的距离.即
小明走的路程+小红走的路程=两家之间的距离(20km).
典例精析
解:(1)设小明与小红骑车走了x h后相遇,
则根据等量关系,得
13x + 12x = 20 .
解得 x = 0.8 .
答:经过0.8 h他们两人相遇.
小明走的路程
小红走的路程
(2)如果小明先走30min,那么小红骑车要走多少小时才能与小明相遇?
小明先走的路程
小红出发后小明走的路程
小红走的路程
解:(2)设小红骑车走了t h后与小明相遇,
则根据等量关系,得
13(0.5 + t )+12t = 20 .
解得 t = 0.54 .
答:小红骑车走0.54h后与小明相遇.
路程=速度×时间
甲走的路程+乙走的路程=甲、乙之间的距离
相遇问题
总结归纳
注意相向而行的始发时间和地点
甲、乙两站相距480千米,一列慢车从甲站开出,每小时行90千米,一列快车从乙站开出,每小时行140千米.慢车先开出1小时,快车再开,两车相向而行.问快车开出多少小时后两车相遇?
练一练
解:设快车开出x小时后两车相遇.
依题意,得: 90×1+90x+140x=480.
解方程,得:
答:快车开出 小时后两车相遇.
工程问题
二
典例精析
例2 一项工作,小李单独做需要6h完成,小王单独做需要9h完成.如果小李先做2h后,再由两人合做,那么还需几小时才能完成 ?
分析:如果设还需两人合做xh才能完成,那么有下面分析图.
小李单独做2h完成的工作量
小王、小李合做xh完成的工作量
总工作量
解:设两人合做x小时才能完成.依题意,得
解得
答:两人合做 小时才能完成这项工作.
生产的这批螺钉、螺母要打包,由一个人做要40 h 完成.现计划由一部分人先做4 h,然后增加 2人与他们一起做8 h,完成这项工作. 假设这些人的工作效率相同,具体应该安排多少人工作?
列表分析:
人均效率 人数 时间 工作量
前一部分工作 x 4
后一部分工作 x+2 8
×
=
×
×
×
=
工作量之和等于总工作量1
试一试
解:设先安排 x 人做4 h,根据题意得等量关系:
可列方程
解方程,得
4x+8(x+2)=40,
4x+8x+16=40,
12x=24,
x=2.
答:应先安排 2人做4 小时.
前部分工作总量+后部分工作总量=总工作量1
解决工程问题的思路:
1.三个基本量:
工程问题中的三个基本量:工作总量、工作效率、工作时间,
它们之间的关系是:工作总量=工作效率×工作时间.
若把工作量看作1,则工作效率=
2.相等关系:
(1)按工作时间,各时间段的工作量之和=完成的工作量.
(2)按工作者,若一项工作有甲、乙两人参与,则甲的工作量
+乙的工作量=完成的工作量.
要点归纳
当堂练习
1.甲、乙两人骑摩托车同时从相距170千米的A,B两地相向而行,2小时相遇,如果甲比乙每小时多行5千米,则乙每小时行( )
A.30千米 B.40千米 C.50千米 D.45千米
2.甲、乙两人在400米的环形跑道上练习长跑,他们同时同地反向而跑,甲的速度是6米/秒,乙的速度是4米/秒,则他们首次相遇时,两人都跑了( )
A.40秒 B.50秒 C.60秒 D.70秒
B
A
3.一项工作,甲独做需18天,乙独做需24天,如果两人合做8天后,余下的工作再由甲独做x天完成,
那么所列方程为____________.
课堂小结
列一元一次方程解决相遇问题、工程问题
相遇问题
工程问题
路程=速度×时间
甲走的路程+乙走的路程=甲、乙之间的距离
甲的工作量+乙的工作量=完成的工作量
各时间段的工作量之和=完成的工作量
工作总量=工作效率×工作时间
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
