人教版九年级上册25.2用列举法求概率课件(共22张PPT)
文档属性
| 名称 | 人教版九年级上册25.2用列举法求概率课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-14 08:26:55 | ||
图片预览







文档简介
(共22张PPT)
人教版九年级数学上册
25.2 用列举法求概率
回答下列问题,并说明理由.
(1)掷一枚硬币,正面向上的概率是_______;
(2)袋子中装有 5 个红球,3 个绿球,这些球除了
颜色外都相同,从袋子中随机摸出一个球,它是红色的
概率为________;
(3)掷一个骰子,观察向上一面的点数,点数大
于 4 的概率为______.
查学诊断
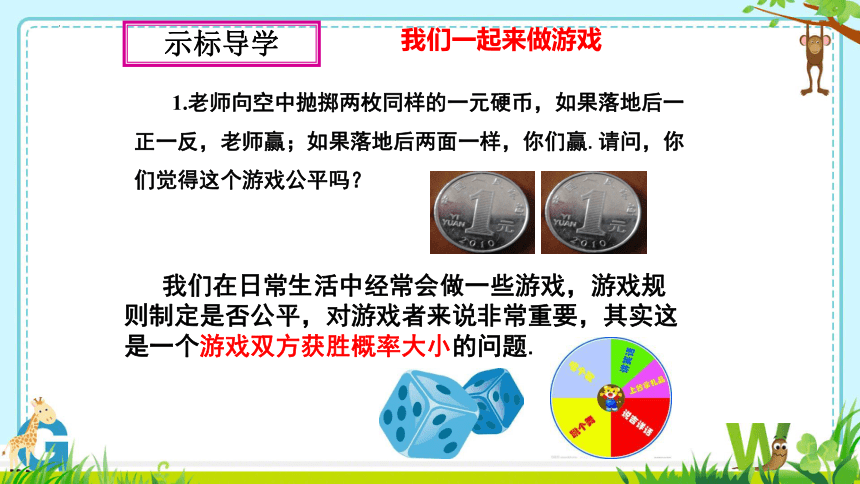
1.老师向空中抛掷两枚同样的一元硬币,如果落地后一正一反,老师赢;如果落地后两面一样,你们赢.请问,你们觉得这个游戏公平吗?
我们一起来做游戏
示标导学
我们在日常生活中经常会做一些游戏,游戏规则制定是否公平,对游戏者来说非常重要,其实这是一个游戏双方获胜概率大小的问题.
用直接列举法求概率
同时掷两枚硬币,试求下列事件的概率:
(1)两枚硬币两面一样的概率;
(2)一枚硬币正面朝上,一枚硬币反面朝上的概率;
①
②
探索交流
导学施教
“掷两枚硬币”所有结果如下:
正正
正反
反正
反反
①
②
①
②
①
②
①
②
解:
(1)两枚硬币两面一样包括两面都是正面,两面都是反面,共两种情形;所以学生赢的概率是
(2)一枚硬币正面朝上,一枚硬币反面朝上,共有反正,正反两种情形;所以老师赢的概率是
∵P(学生赢)=P(老师赢).
∴这个游戏是公平的.
上述这种列举法我们称为直接列举法,即把事件可能出现的结果一一列出.
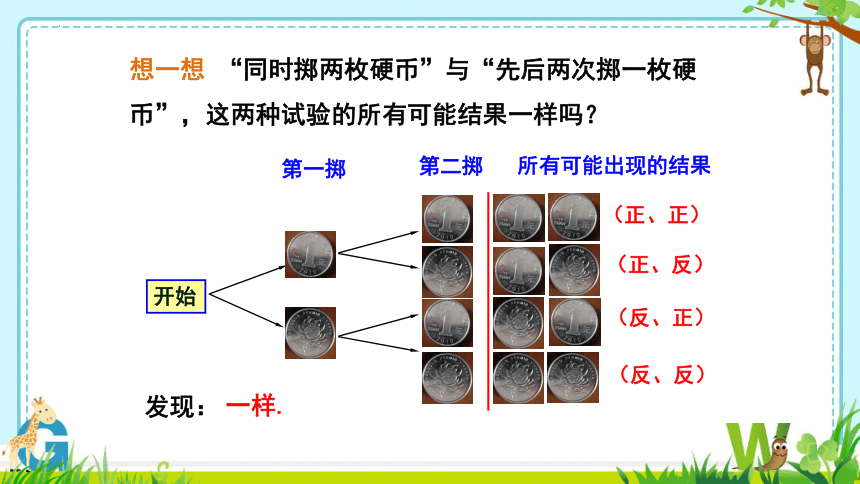
想一想 “同时掷两枚硬币”与“先后两次掷一枚硬币”,这两种试验的所有可能结果一样吗?
开始
第一掷
第二掷
所有可能出现的结果
(正、正)
(正、反)
(反、正)
(反、反)
发现:
一样.
随机事件“同时”与“先后”的关系:“两个相同的随机事件同时发生”与 “一个随机事件先后两次发生”的结果是一样的.
归纳总结
问题2 怎样列表格?
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
列表法中表格构造特点:
两枚硬币分别记为第 1 枚和第 2 枚,可以用下表列举出所有可能出现的结果.
正 反
正 (正,正) (反,正)
反 (正,反) (反,反)
第 1 枚
第 2 枚
由此表可以看出,同时抛掷两枚硬币,可能出现的结果有 4 个,并且它们出现的可能性相等.
列表法:
上述这种列举法我们称为列表法,用表格的形式反映事件发生的各种结果出现的次数,以及某一事件发生的可能的可能的次数和方式。
注意
当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多时,为不重不漏地列出所有可能结果,通常采用列表法.
例1 同时抛掷2枚均匀的骰子一次,骰子各面上的点数分别是1,2,···,6.试分别计算如下各随机事件的概率.(用列表法求概率)
(1)抛出的点数之和等于8;
(2)抛出的点数之和等于12.
变式: (1)两枚骰子的点数相同;
(2)两枚骰子点数的和是 9;
(3)至少有一枚骰子的点数为 2.
练测促学
第2枚
骰子
第1枚骰子
结
果
1
2
3
4
5
6
1
2
3
4
5
6
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
(4,2)
(5,2)
(6,2)
(4,3)
(5,3)
(6,3)
(4,4)
(5,4)
(6,4)
(4,5)
(5,5)
(6,5)
(4,6)
(5,6)
(6,6)
一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,两次都摸出红球的概率是多少?
1
2
拓展延伸
结果
第一次
第二次
解:利用表格列出所有可能的结果:
白
红1
红2
白
红1
红2
(白,白)
(白,红1)
(白,红2)
(红1,白)
(红1,红1)
(红1,红2)
(红2,白)
(红2,红1)
(红2,红2)
变式:一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后不再放回袋中,再从中任意摸出一个球,两次都摸出红球的概率是多少?
解:利用表格列出所有可能的结果:
白
红1
红2
白
红1
红2
(白,红1)
(白,红2)
(红1,白)
(红1,红2)
(红2,白)
(红2,红1)
结果
第一次
第二次
列举法
关键
常用
方法
直接列举法
列表法
画树状图法
(下节课学习)
适用对象
两个试验因素或分两步进行的试验.
基本步骤
列表;
确定m、n值
代入概率公式计算.
在于正确列举出试验结果的各种可能性.
确保试验中每种结果出现的可能性大小相等.
前提条件
课堂小结
当堂检测
1.小明与小红玩一次“石头、剪刀、布”游戏,则小明赢的概率是( )
2.某次考试中,每道单项选择题一般有4个选项,某同学有两道题不会做,于是他以“抓阄”的方式选定其中一个答案,则该同学的这两道题全对的概率是( )
C
D
A. B. C. D.
A. B. C. D.
3.如果有两组牌,它们的牌面数字分别是1,2,3,那么从每组牌中各摸出一张牌.
(1)摸出两张牌的数字之和为4的概念为多少?
(2)摸出为两张牌的数字相等的概率为多少?
4、一个不透明的布袋子里装有 4 个大小、质地
均相同的乒乓球,球面上分别标有 1,2,3,4.小林和
小华按照以下方式抽取乒乓球:先从布袋中随机抽取一
个乒乓球,记下标号后放回袋内搅匀,再从布袋内随机
抽取第二个乒乓球,记下标号,求出两次取的小球的标
号之和.若标号之和为 4,小林赢;若标号之和为 5,
小华赢.请判断这个游戏是否公平,并说明理由.
教科书 139 页 练习.
预习作业:
布置作业
人教版九年级数学上册
25.2 用列举法求概率
回答下列问题,并说明理由.
(1)掷一枚硬币,正面向上的概率是_______;
(2)袋子中装有 5 个红球,3 个绿球,这些球除了
颜色外都相同,从袋子中随机摸出一个球,它是红色的
概率为________;
(3)掷一个骰子,观察向上一面的点数,点数大
于 4 的概率为______.
查学诊断
1.老师向空中抛掷两枚同样的一元硬币,如果落地后一正一反,老师赢;如果落地后两面一样,你们赢.请问,你们觉得这个游戏公平吗?
我们一起来做游戏
示标导学
我们在日常生活中经常会做一些游戏,游戏规则制定是否公平,对游戏者来说非常重要,其实这是一个游戏双方获胜概率大小的问题.
用直接列举法求概率
同时掷两枚硬币,试求下列事件的概率:
(1)两枚硬币两面一样的概率;
(2)一枚硬币正面朝上,一枚硬币反面朝上的概率;
①
②
探索交流
导学施教
“掷两枚硬币”所有结果如下:
正正
正反
反正
反反
①
②
①
②
①
②
①
②
解:
(1)两枚硬币两面一样包括两面都是正面,两面都是反面,共两种情形;所以学生赢的概率是
(2)一枚硬币正面朝上,一枚硬币反面朝上,共有反正,正反两种情形;所以老师赢的概率是
∵P(学生赢)=P(老师赢).
∴这个游戏是公平的.
上述这种列举法我们称为直接列举法,即把事件可能出现的结果一一列出.
想一想 “同时掷两枚硬币”与“先后两次掷一枚硬币”,这两种试验的所有可能结果一样吗?
开始
第一掷
第二掷
所有可能出现的结果
(正、正)
(正、反)
(反、正)
(反、反)
发现:
一样.
随机事件“同时”与“先后”的关系:“两个相同的随机事件同时发生”与 “一个随机事件先后两次发生”的结果是一样的.
归纳总结
问题2 怎样列表格?
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
列表法中表格构造特点:
两枚硬币分别记为第 1 枚和第 2 枚,可以用下表列举出所有可能出现的结果.
正 反
正 (正,正) (反,正)
反 (正,反) (反,反)
第 1 枚
第 2 枚
由此表可以看出,同时抛掷两枚硬币,可能出现的结果有 4 个,并且它们出现的可能性相等.
列表法:
上述这种列举法我们称为列表法,用表格的形式反映事件发生的各种结果出现的次数,以及某一事件发生的可能的可能的次数和方式。
注意
当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多时,为不重不漏地列出所有可能结果,通常采用列表法.
例1 同时抛掷2枚均匀的骰子一次,骰子各面上的点数分别是1,2,···,6.试分别计算如下各随机事件的概率.(用列表法求概率)
(1)抛出的点数之和等于8;
(2)抛出的点数之和等于12.
变式: (1)两枚骰子的点数相同;
(2)两枚骰子点数的和是 9;
(3)至少有一枚骰子的点数为 2.
练测促学
第2枚
骰子
第1枚骰子
结
果
1
2
3
4
5
6
1
2
3
4
5
6
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
(4,2)
(5,2)
(6,2)
(4,3)
(5,3)
(6,3)
(4,4)
(5,4)
(6,4)
(4,5)
(5,5)
(6,5)
(4,6)
(5,6)
(6,6)
一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,两次都摸出红球的概率是多少?
1
2
拓展延伸
结果
第一次
第二次
解:利用表格列出所有可能的结果:
白
红1
红2
白
红1
红2
(白,白)
(白,红1)
(白,红2)
(红1,白)
(红1,红1)
(红1,红2)
(红2,白)
(红2,红1)
(红2,红2)
变式:一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后不再放回袋中,再从中任意摸出一个球,两次都摸出红球的概率是多少?
解:利用表格列出所有可能的结果:
白
红1
红2
白
红1
红2
(白,红1)
(白,红2)
(红1,白)
(红1,红2)
(红2,白)
(红2,红1)
结果
第一次
第二次
列举法
关键
常用
方法
直接列举法
列表法
画树状图法
(下节课学习)
适用对象
两个试验因素或分两步进行的试验.
基本步骤
列表;
确定m、n值
代入概率公式计算.
在于正确列举出试验结果的各种可能性.
确保试验中每种结果出现的可能性大小相等.
前提条件
课堂小结
当堂检测
1.小明与小红玩一次“石头、剪刀、布”游戏,则小明赢的概率是( )
2.某次考试中,每道单项选择题一般有4个选项,某同学有两道题不会做,于是他以“抓阄”的方式选定其中一个答案,则该同学的这两道题全对的概率是( )
C
D
A. B. C. D.
A. B. C. D.
3.如果有两组牌,它们的牌面数字分别是1,2,3,那么从每组牌中各摸出一张牌.
(1)摸出两张牌的数字之和为4的概念为多少?
(2)摸出为两张牌的数字相等的概率为多少?
4、一个不透明的布袋子里装有 4 个大小、质地
均相同的乒乓球,球面上分别标有 1,2,3,4.小林和
小华按照以下方式抽取乒乓球:先从布袋中随机抽取一
个乒乓球,记下标号后放回袋内搅匀,再从布袋内随机
抽取第二个乒乓球,记下标号,求出两次取的小球的标
号之和.若标号之和为 4,小林赢;若标号之和为 5,
小华赢.请判断这个游戏是否公平,并说明理由.
教科书 139 页 练习.
预习作业:
布置作业
同课章节目录
