人教版九年级上册23.1图形的旋转课件(共19张PPT)
文档属性
| 名称 | 人教版九年级上册23.1图形的旋转课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-14 08:43:18 | ||
图片预览




文档简介
(共19张PPT)
23.1图形的旋转(第一课时)
第二十三章 旋转
学习目标:
1.通过观察具体实例认识旋转,归纳旋转的概念;
2.探究旋转的性质,会画出旋转后的图形.
学习重点:1.旋转的概念
2.旋转性质的探究过程及其应用.
学习难点:旋转性质的归纳
23.1图形的旋转(第一课时)
导入新课
问题1:以下这些转动现象有什么共同的特征?
问题2:这些图形在转动的过程中,其形状、
大小、位置是否发生改变
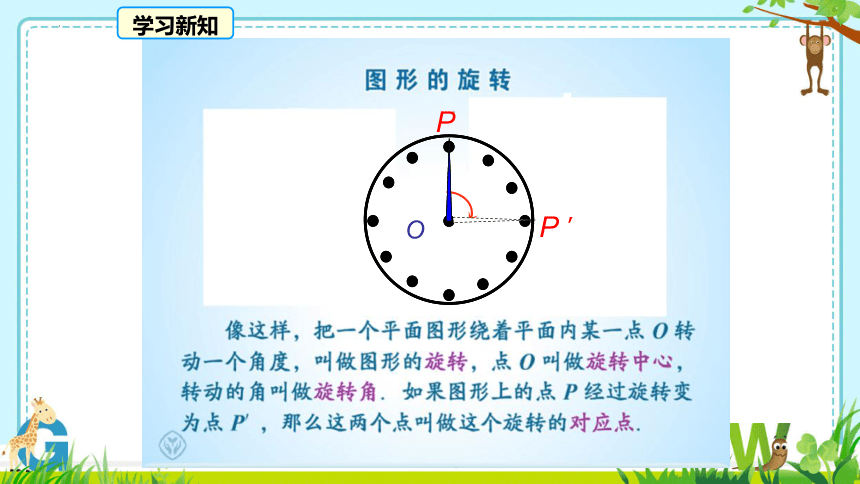
学习新知
O
P
P'
开始/暂停
奖品区
(1)
A
C
B
(3)
A
B
C
(2)
A
B
C
A
C
B
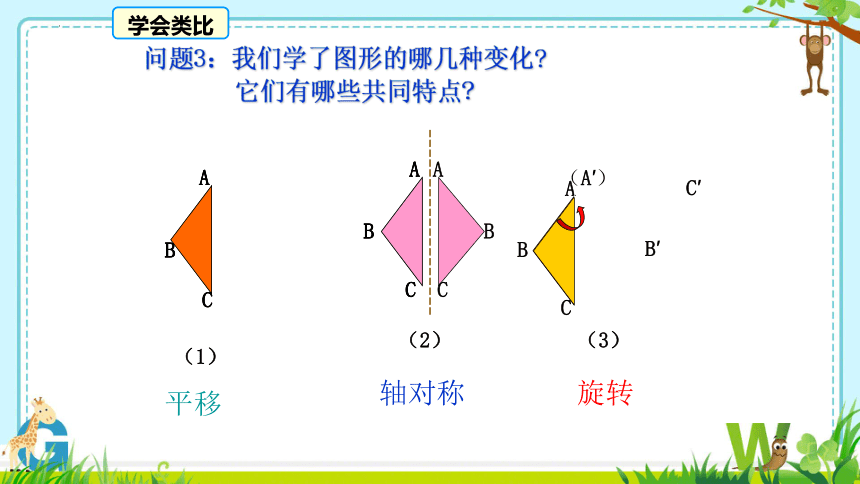
问题3:我们学了图形的哪几种变化
平移
轴对称
旋转
A
B
C
A
B
C
(A′)
B′
C′
学会类比
它们有哪些共同特点
动手操作
请同学们拿出硬纸板,按照下面的步骤进行操作:
(1)在硬纸板上,挖出一个三角形,再另挖一个小洞;
(2)把硬纸板放在一张白纸上,在白纸上描出挖掉的三角形图案,记为△ABC;再描出小洞,记为点O
(3)将硬纸板围绕点O转动一个角度,再描出这个挖掉的三角形,记为△A B C ;
(4)移开硬纸板.
合作探究
请同学们进行观察、探究,分组讨论,共同合作,解决以下问题:
(1)分别连结OA、OA ,则OA OA (填><=)
(2)再连结OB、OB , 则
∠AOA ∠BOB (填><=)
(3)△ABC 和△A B C 的形状和
大小有什么关系?
(4)你还能发现哪些有类似关系的
线段和角?这一发现对于任意三角形
的任意旋转都成立吗?试着归纳旋转
的性质.
验证猜想
学以致用
如图,△ABC 是等边三角形,P 是△ABC 内一点.△APC 沿顺时针方向旋转后与△AP′B重合,
最小旋转角等于________度.
变式1:若AP=1cm,则PP'= cm.
变式2:若BC为2cm,则五边形AP BCP的面积为______.
例1图
方法点拨:旋转角的问题,应根据条件寻找对应点, 对
应点与旋转中心连线段的夹角就是对应角。
课堂小结
1.通过这节课的学习,你们有什么收获吗?
2.对于图形的旋转,你还有什么疑问吗?
布置作业
“导学案”的“课后检测”
1. 如图,一块等腰直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到△A'B'C的位置,则旋转角为
°
2.如图,将△ABC绕点A逆时针旋转110°,得到△ADE,
若点D落在线段BC的延长线上,则∠B大小为( )
A.30° B.35° C.40° D.45°
第2题图
第1题图
3.如图, △ABC中, ∠C=90 °,将△ABC绕点B逆时针旋转90 °,得到△A'BC'。若BC=3,AC=4,点A旋转后的对应点为A ,求AA 的长。
(选做题)4.在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心是______.
P1
(选做题)5.上图为 4×4 的正方形网格,每个小正方形的边长均为 1,将 △OAB 绕点 O 逆时针旋转 90°, 你能画出△OAB 旋转后的图形 △OA'B'吗?
A
B
O
谢 谢!
学以致用
请回答:下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
C
√
√
√
√
学以致用
请回答:如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
旋转中心是点O
旋转角是∠AOA'或∠BOB'
请回答:如图,△ABO绕着点O旋转得到△CDO,则旋转中心是点 ,点A的对应点是点 ;点B的对应点是点 ;线段OA的对应线段是 ;线段OB的对应线段是 ;旋转角是 ;
学以致用
O
C
D
OC
OD
∠AOC或∠BOD
23.1图形的旋转(第一课时)
第二十三章 旋转
学习目标:
1.通过观察具体实例认识旋转,归纳旋转的概念;
2.探究旋转的性质,会画出旋转后的图形.
学习重点:1.旋转的概念
2.旋转性质的探究过程及其应用.
学习难点:旋转性质的归纳
23.1图形的旋转(第一课时)
导入新课
问题1:以下这些转动现象有什么共同的特征?
问题2:这些图形在转动的过程中,其形状、
大小、位置是否发生改变
学习新知
O
P
P'
开始/暂停
奖品区
(1)
A
C
B
(3)
A
B
C
(2)
A
B
C
A
C
B
问题3:我们学了图形的哪几种变化
平移
轴对称
旋转
A
B
C
A
B
C
(A′)
B′
C′
学会类比
它们有哪些共同特点
动手操作
请同学们拿出硬纸板,按照下面的步骤进行操作:
(1)在硬纸板上,挖出一个三角形,再另挖一个小洞;
(2)把硬纸板放在一张白纸上,在白纸上描出挖掉的三角形图案,记为△ABC;再描出小洞,记为点O
(3)将硬纸板围绕点O转动一个角度,再描出这个挖掉的三角形,记为△A B C ;
(4)移开硬纸板.
合作探究
请同学们进行观察、探究,分组讨论,共同合作,解决以下问题:
(1)分别连结OA、OA ,则OA OA (填><=)
(2)再连结OB、OB , 则
∠AOA ∠BOB (填><=)
(3)△ABC 和△A B C 的形状和
大小有什么关系?
(4)你还能发现哪些有类似关系的
线段和角?这一发现对于任意三角形
的任意旋转都成立吗?试着归纳旋转
的性质.
验证猜想
学以致用
如图,△ABC 是等边三角形,P 是△ABC 内一点.△APC 沿顺时针方向旋转后与△AP′B重合,
最小旋转角等于________度.
变式1:若AP=1cm,则PP'= cm.
变式2:若BC为2cm,则五边形AP BCP的面积为______.
例1图
方法点拨:旋转角的问题,应根据条件寻找对应点, 对
应点与旋转中心连线段的夹角就是对应角。
课堂小结
1.通过这节课的学习,你们有什么收获吗?
2.对于图形的旋转,你还有什么疑问吗?
布置作业
“导学案”的“课后检测”
1. 如图,一块等腰直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到△A'B'C的位置,则旋转角为
°
2.如图,将△ABC绕点A逆时针旋转110°,得到△ADE,
若点D落在线段BC的延长线上,则∠B大小为( )
A.30° B.35° C.40° D.45°
第2题图
第1题图
3.如图, △ABC中, ∠C=90 °,将△ABC绕点B逆时针旋转90 °,得到△A'BC'。若BC=3,AC=4,点A旋转后的对应点为A ,求AA 的长。
(选做题)4.在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心是______.
P1
(选做题)5.上图为 4×4 的正方形网格,每个小正方形的边长均为 1,将 △OAB 绕点 O 逆时针旋转 90°, 你能画出△OAB 旋转后的图形 △OA'B'吗?
A
B
O
谢 谢!
学以致用
请回答:下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
C
√
√
√
√
学以致用
请回答:如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
旋转中心是点O
旋转角是∠AOA'或∠BOB'
请回答:如图,△ABO绕着点O旋转得到△CDO,则旋转中心是点 ,点A的对应点是点 ;点B的对应点是点 ;线段OA的对应线段是 ;线段OB的对应线段是 ;旋转角是 ;
学以致用
O
C
D
OC
OD
∠AOC或∠BOD
同课章节目录
