人教版九年级上册22.1.4二次函数y=ax2 bx c的图象和性质课件(共23张PPT)
文档属性
| 名称 | 人教版九年级上册22.1.4二次函数y=ax2 bx c的图象和性质课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-14 08:45:31 | ||
图片预览







文档简介
(共23张PPT)
22.1.4 二次函数
的图象和性质
y=ax2+bx+c
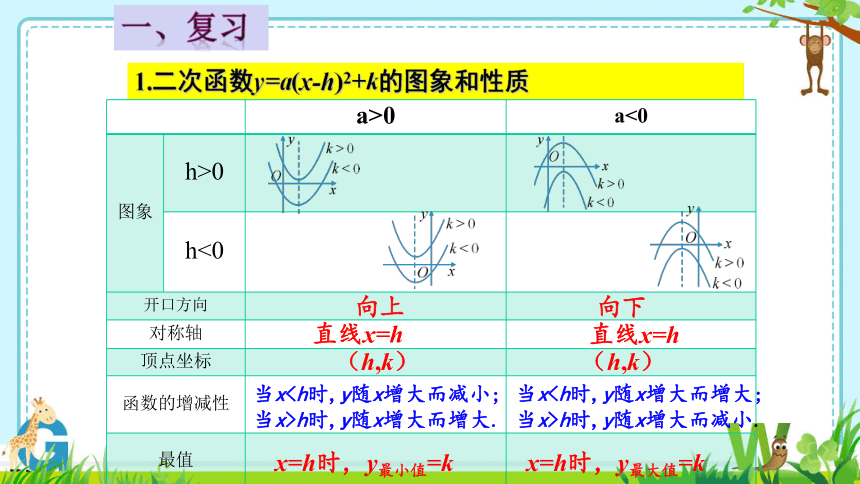
1.二次函数y=a(x-h)2+k的图象和性质
一、复习
a>0 a<0
图象 h>0
h<0
开口方向
对称轴
顶点坐标
函数的增减性
最值
当xh时,y随x增大而减小.
当xh时,y随x增大而增大.
向上
向下
直线x=h
直线x=h
(h,k)
x=h时,y最小值=k
x=h时,y最大值=k
(h,k)
二、学习目标:
1.理解二次函数 y = ax 2 + bx + c 与 之间
的联系,体会转化思想;
2.通过图象了解二次函数 y = ax 2 + bx + c 的性质,体
会数形结合的思想.
3 .会求二次函数的最值,并能利用它解决简单的实际问题.
学习重点:
会用配方法将数字系数的二次函数的表达式化为 y =
的形式,并能由此得到二次函数 y = ax 2
+ bx + c 的图象和性质.
(x - h) + k
y = a
2
(x - h) + k
2
a
问题:
当一枚火箭被竖直向上发射时,它的高度 h (m) 与时间 t (s) 的关系可以用公式 h = - 5 t + 150 t +10 表示,经过多长时间,火箭到达它的最高点?最高点的高度是多少?
今天我们继续学习:
二次函数的一般形式y=ax2+bx+c(a≠0)的图象和性质
同学们想知道如何求这道题吗?
配方得:
y= x2-6x+21
=
(x-6)2+3
由此可知,抛物线
的顶点是点(6,3),对称轴是直线 x=6.
y= x2-6x+21
我们已经知道, 这样的函数图像和性质,能否利用这些知识来讨论二次函数 的图像和性质 ?
探究一
三、新课
(具体书写板演过程)
根据顶点式确定开口方向,对称轴,顶点坐标.
x … 3 4 5 6 7 8 9 …
… …
列表:利用图像的对称性,选取x适当的值列表计算.
… 7.5 5 3.5 3 3.5 5 7.5 …
∵a= >0,
∴开口向上;
对称轴:直线x=6;
顶点坐标:(6,3).
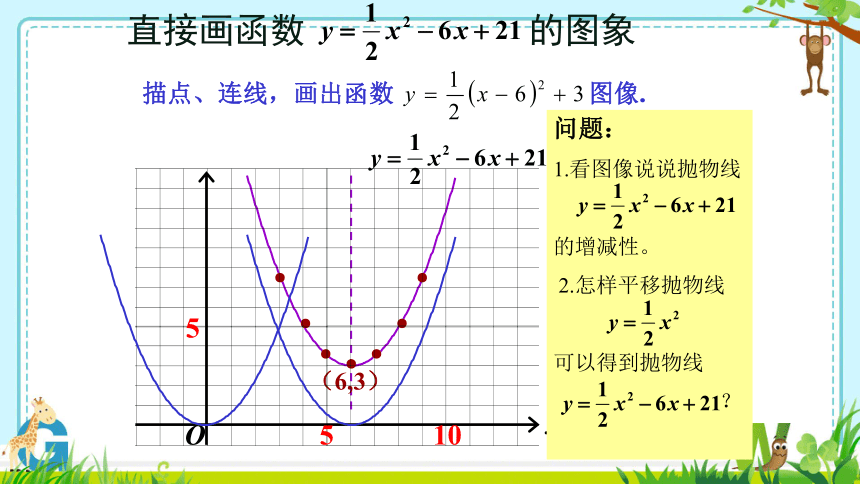
直接画函数 的图象
直接画函数 的图象
描点、连线,画出函数 图像.
●
●
●
●
●
●
●
(6,3)
O
x
5
5
10
问题:
1.看图像说说抛物线
的增减性。
2.怎样平移抛物线
可以得到抛物线
?
探究二
研究二次函数一般式y=ax2+bx+c的图象,关键是找到对称轴和顶点坐标。通常利用配方法把二次函数y=ax2+bx+c转化为y=a(x-h) +k的形式,然后确定抛物线的开口方向、对称轴和顶点。
1 用配方法求二次函数y=ax +bx+c的对称轴和顶点坐标.
函数y=ax2+bx+c的配成顶点式
配方法:
归纳
抛物线y=ax2+bx+c (a≠0)
=a(x+ )2+
因此,抛物线y=ax2+bx+c 的对称轴是
x=-
顶点坐标是(- , )
识记
图象的画法.
步骤:1.利用配方法或公式法把
化为
的形式。
2.确定抛物线的开口方向、对称轴及顶点坐标。
3.在对称轴的两侧以顶点为中心左右对称描点画图。
利用函数y=ax2+bx+c的顶点式来求最值
快速反应:火箭被竖直向上发射时,它的高度 h (m) 与时间 t (s) 的关系为h = - 5 t + 150 t +10 经过多长时间,火箭到达它的最高点?最高点的高度是多少?
答:经过15秒,火箭到达最高点,起最大高度为1135米。
总结:求二次函数最值,有两个方法.
(1)用配方法;(2)用公式法.
(3)开口方向:当 a>0时,抛物线开口向上;当 a<0时,抛物线开口向下。
二次函数
的性质:
(1)顶点坐标
(2)对称轴是直线
四、课堂小结
如果a>0,当
时,函数有最小值,
如果a<0,当
时,函数有最大值,
(4)最值:
①若a>0,当
时,y随x的增大而增大;
当
时,y随x的增大而减小。
②若a<0,当
时,y随x的增大而减小;
当
时,y随x的增大而增大。
(5)增减性:
1.确定下列抛物线的开口方向、对称轴及顶点坐标.
(1)y=-3x2+12x-3;(2)y=4x2-24x+26;
(3)y=2x2+8x-6; (4)y=12x2-48x+45.
a=4>0,开口向上,
对称轴为x=3,
顶点为(3,-10).
a=-3<0,开口向下,
对称轴为x=2,
顶点为(2,9).
a=2>0,开口向上,
对称轴为x=-2
顶点为(-2,-14).
a=12>0,开口向上,
对称轴为x=2,
顶点为(2,-3).
五、巩固练习
2.已知函数y=-2x2+x-4,当x= 时,y的最大值为 .
3.已知二次函数y=x2-2x+1,那么它的图象大致为( )
B
函数y=ax2+bx+c(a≠0)的应用
某服装公司试销一种成本为每件50元的T恤衫,规定试销时的销售单价不低于成本价,又不高于每件70元,试销中销售量y(件)与销售单价x(元)的关系可以近似的看作一次函数(如图).
(1)求y与x之间的函数关系式;
(2)设公司获得的总利润(总利润=总销售额-总成本)为P元,求P与x之间的函数关系式,并写出自变量x的取值范围;根据题意判断:当x取何值时,P的值最大?最大值是多少?
400
300
60
70
O
y(件)
x(元)
六、中考链接
解:(1)设y与x之间的函数关为
∵经过(60,400)(70,300)
∴
解得:
∴y与x之间的函数关系式为
(2)P=(-10x+1000)(x-50)=
∴当x=75时,P最大,最大利润为6250元
22.1.4 二次函数
的图象和性质
y=ax2+bx+c
1.二次函数y=a(x-h)2+k的图象和性质
一、复习
a>0 a<0
图象 h>0
h<0
开口方向
对称轴
顶点坐标
函数的增减性
最值
当x
当x
向上
向下
直线x=h
直线x=h
(h,k)
x=h时,y最小值=k
x=h时,y最大值=k
(h,k)
二、学习目标:
1.理解二次函数 y = ax 2 + bx + c 与 之间
的联系,体会转化思想;
2.通过图象了解二次函数 y = ax 2 + bx + c 的性质,体
会数形结合的思想.
3 .会求二次函数的最值,并能利用它解决简单的实际问题.
学习重点:
会用配方法将数字系数的二次函数的表达式化为 y =
的形式,并能由此得到二次函数 y = ax 2
+ bx + c 的图象和性质.
(x - h) + k
y = a
2
(x - h) + k
2
a
问题:
当一枚火箭被竖直向上发射时,它的高度 h (m) 与时间 t (s) 的关系可以用公式 h = - 5 t + 150 t +10 表示,经过多长时间,火箭到达它的最高点?最高点的高度是多少?
今天我们继续学习:
二次函数的一般形式y=ax2+bx+c(a≠0)的图象和性质
同学们想知道如何求这道题吗?
配方得:
y= x2-6x+21
=
(x-6)2+3
由此可知,抛物线
的顶点是点(6,3),对称轴是直线 x=6.
y= x2-6x+21
我们已经知道, 这样的函数图像和性质,能否利用这些知识来讨论二次函数 的图像和性质 ?
探究一
三、新课
(具体书写板演过程)
根据顶点式确定开口方向,对称轴,顶点坐标.
x … 3 4 5 6 7 8 9 …
… …
列表:利用图像的对称性,选取x适当的值列表计算.
… 7.5 5 3.5 3 3.5 5 7.5 …
∵a= >0,
∴开口向上;
对称轴:直线x=6;
顶点坐标:(6,3).
直接画函数 的图象
直接画函数 的图象
描点、连线,画出函数 图像.
●
●
●
●
●
●
●
(6,3)
O
x
5
5
10
问题:
1.看图像说说抛物线
的增减性。
2.怎样平移抛物线
可以得到抛物线
?
探究二
研究二次函数一般式y=ax2+bx+c的图象,关键是找到对称轴和顶点坐标。通常利用配方法把二次函数y=ax2+bx+c转化为y=a(x-h) +k的形式,然后确定抛物线的开口方向、对称轴和顶点。
1 用配方法求二次函数y=ax +bx+c的对称轴和顶点坐标.
函数y=ax2+bx+c的配成顶点式
配方法:
归纳
抛物线y=ax2+bx+c (a≠0)
=a(x+ )2+
因此,抛物线y=ax2+bx+c 的对称轴是
x=-
顶点坐标是(- , )
识记
图象的画法.
步骤:1.利用配方法或公式法把
化为
的形式。
2.确定抛物线的开口方向、对称轴及顶点坐标。
3.在对称轴的两侧以顶点为中心左右对称描点画图。
利用函数y=ax2+bx+c的顶点式来求最值
快速反应:火箭被竖直向上发射时,它的高度 h (m) 与时间 t (s) 的关系为h = - 5 t + 150 t +10 经过多长时间,火箭到达它的最高点?最高点的高度是多少?
答:经过15秒,火箭到达最高点,起最大高度为1135米。
总结:求二次函数最值,有两个方法.
(1)用配方法;(2)用公式法.
(3)开口方向:当 a>0时,抛物线开口向上;当 a<0时,抛物线开口向下。
二次函数
的性质:
(1)顶点坐标
(2)对称轴是直线
四、课堂小结
如果a>0,当
时,函数有最小值,
如果a<0,当
时,函数有最大值,
(4)最值:
①若a>0,当
时,y随x的增大而增大;
当
时,y随x的增大而减小。
②若a<0,当
时,y随x的增大而减小;
当
时,y随x的增大而增大。
(5)增减性:
1.确定下列抛物线的开口方向、对称轴及顶点坐标.
(1)y=-3x2+12x-3;(2)y=4x2-24x+26;
(3)y=2x2+8x-6; (4)y=12x2-48x+45.
a=4>0,开口向上,
对称轴为x=3,
顶点为(3,-10).
a=-3<0,开口向下,
对称轴为x=2,
顶点为(2,9).
a=2>0,开口向上,
对称轴为x=-2
顶点为(-2,-14).
a=12>0,开口向上,
对称轴为x=2,
顶点为(2,-3).
五、巩固练习
2.已知函数y=-2x2+x-4,当x= 时,y的最大值为 .
3.已知二次函数y=x2-2x+1,那么它的图象大致为( )
B
函数y=ax2+bx+c(a≠0)的应用
某服装公司试销一种成本为每件50元的T恤衫,规定试销时的销售单价不低于成本价,又不高于每件70元,试销中销售量y(件)与销售单价x(元)的关系可以近似的看作一次函数(如图).
(1)求y与x之间的函数关系式;
(2)设公司获得的总利润(总利润=总销售额-总成本)为P元,求P与x之间的函数关系式,并写出自变量x的取值范围;根据题意判断:当x取何值时,P的值最大?最大值是多少?
400
300
60
70
O
y(件)
x(元)
六、中考链接
解:(1)设y与x之间的函数关为
∵经过(60,400)(70,300)
∴
解得:
∴y与x之间的函数关系式为
(2)P=(-10x+1000)(x-50)=
∴当x=75时,P最大,最大利润为6250元
同课章节目录
