人教版八年级上册14.1.1同底数幂的乘法课件(共24张PPT)
文档属性
| 名称 | 人教版八年级上册14.1.1同底数幂的乘法课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 996.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-14 09:05:49 | ||
图片预览



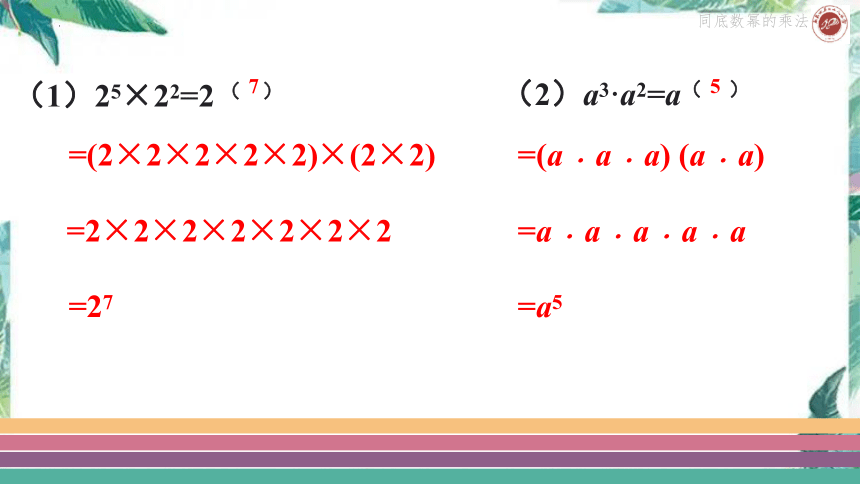




文档简介
(共24张PPT)
同底数幂的乘法
14.1.1
人教版八年级数学上册
地球,是太阳系中的一颗行星,地球绕着太阳转;太阳是一颗恒星,太阳光的速度约是3×108 米/秒,照射到地球表面所需时间约是5×102 秒,地球与太阳之间的距离约是多少米
〖想一想〗你会列式吗?
列出的算式:(3×108)×(5×102)
=(3×5)×(108×102)
你会计算吗? 108×102=
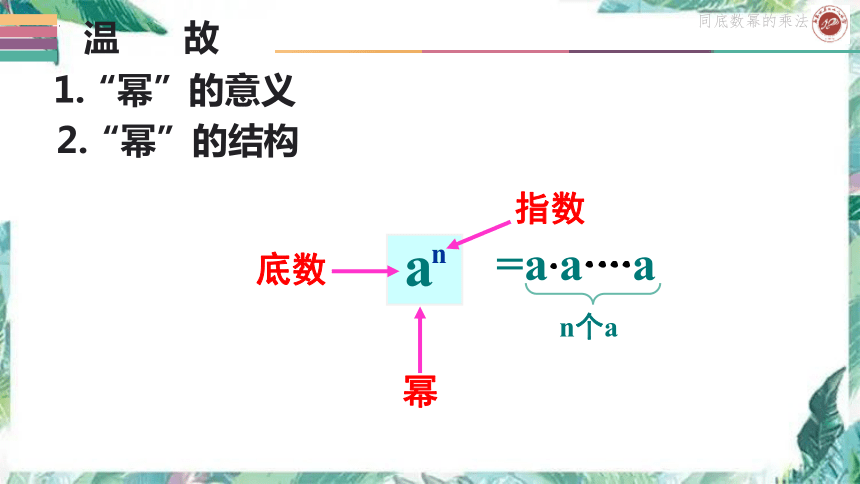
温 故
a
n
指数
幂
底数
=a·a····a
n个a
1.“幂”的意义
2.“幂”的结构
做一做
108×102= ?
108× 102
=(10×···× 10 )×( 10×10 )
8个10
= 10×10×···×10
10个10
=1010
(乘方的意义)
(乘法的结合律)
(乘方的意义)
(1)25×22=2 ( )
=(2×2×2×2×2)
×(2×2)
=2×2×2×2×2×2×2
=27
(2)a3·a2=a( )
=(a﹒a﹒a) (a﹒a)
=a﹒a﹒a﹒a﹒a
=a5
7
5
(3)5m× 5n =5( )
=(5×5×5×…×5)
m个5
×(5×5×5 ×…×5)
n个5
=5×5×…×5
(m+n)个5
=5m+n
猜一猜
am · an =a( )
m+n
m+n
(1)25×22=2 ( )
(2)a3·a2=a( )
7
5
猜想:am · an= am+n (m、n都是正整数)
am · an =
m个a
n个a
(aa···a)
= aa···a
=am+n
(m+n)个a
即
am · an = am+n (m、n都是正整数)
(aa···a)
(乘方的意义)
(乘法结合律)
(乘方的意义)
·
知 新
证 明
观 察: am · an = am+n (m、n是正整数)
等式左边是什么运算?有什么特征?
同底数幂的乘法
相同, 是正整数
等式右边是怎样体现同底数幂乘法性质的?
底数不变,指数相加
条件:①乘法
②同底数幂
结果:①底数不变
②指数相加
底数 指数
底数 指数
am · an = am+n (m、n都是正整数)
同底数幂相乘,底数不变,指数相加.
同底数幂的乘法的性质:
符号语言
文字语言
我们在“知新”的路上体会到:“特殊 一般”的心路历程
我们可以直接利用它进行计算.
运 用
范 例
例1 计算:
(1)x2 · x5 ;
(2)a · a6;
解: (1)x2 · x5= x2+5 =x7
a=a1
(1)b3·b3=2b3 (2)b3+b3=b6 (3)(-x)4·(-x)4=(-x)16 (4)n3·n7=n10 (5)a2+a5=a7 (6)y5·y4=y20 (7)x·x2=x2 (8)b4·b4=2b4
辨一辨
判断正误(拿出你们的答题器,开始你们的作答)
算一算
(1) 108×102
(2) x5·x5
(3)-a3·(-a)6
(4) (-2)8 ×(-2)7
(5) xm · x3m+1
(6) a · a6 · a3
= a7 · a3 =a10
例如:
我们在“运用”的路上体会到:“一般 特殊”的思考方式的心路历程
am· an· ap = am+n+p (m、n、p都是正整数)
am·an·ap
=(a·a· … ·a)(a·a· … ·a)(a·a· … ·a)
n个a
m个a
p个a
=am+n+p
猜 想
证 明
推论一
这一性质可以推广到多个同底数幂相乘的情况:
am· an· ap = am+n+p (m、n、p都是正整数)
结 论
(m,n……p都是正整数).
am+n = am·an
(a·a· … ·a)(a·a· … ·a)
m个a
n个a
= am·an=右边
证 明
反过来想一想:当m、n都是正整数时,则am+n = am · an对吗?
推论二
am+n = am · an (m、n都是正整数)
结 论
( m+n)个a
左边=am+n =(a·a· … ·a)
=
这些拓展,在今后的数学学习中运用是很广泛的,你会了吗?
1.若x·xm·x4=x7,则m=____.
试一试
2.填一填:若xm =3 ,xn =2,那么,
(1)xm+n = × = × = ;
(2)x2m = × = × = ;
(3)x2m+n = × = × = .
xm
xn
6
3
2
xm
xm
3
3
9
x2m
xn
9
2
18
实际上,关于同底数幂的运算还有许多的拓展呢。比如:
3.计算:
4.计算: (m是正整数)
A
A
今天我们学了什么?
今天我们悟到什么?
今天的质疑和发现?
升 华
特殊
一般
特殊
例子
应用
公式
拓展思维的宽度,深华思考的层次是成为一代“学霸”的路径.
延 续
巩固性作业(必做)
(1)计算
①c·c11; ②104×102×10; ③(-b)3·(-b)2;
④-b3·b2; ⑤xm-1·xm+1(m>1); ⑥a·a3·an.
(2)已知am=2,an=8,求am+n.
延 续
拓展性作业(希望做)
(1)已知:am=2, an=3, 求a m+n的值。
(2)如果an-2an+1=a11,求n的值。
(3)3×27×9 =3x,求x的值。
(4)已知:a2 ·a6 = 28, 求a的值。
(6)如果xm-n·x2n+1= xn,且ym-1·y4-n= y7,
求m和n的值。
延 续
放飞性作业(鼓励做)
研究性作业 (小组合作完成):请收集有关同底数幂乘法的精彩中考题
阅读性作业(至少读一本):在第十四章“整式的乘法与因式分解”阶段的学习期间,
推荐如下参考书目:
1. 《乘法公式的乾坤大挪移》(储平)(上海科技出版社)
2. 《因式分解技巧》(单 墫)(华东师范大学出版社)
谢谢聆听
同底数幂的乘法
14.1.1
人教版八年级数学上册
地球,是太阳系中的一颗行星,地球绕着太阳转;太阳是一颗恒星,太阳光的速度约是3×108 米/秒,照射到地球表面所需时间约是5×102 秒,地球与太阳之间的距离约是多少米
〖想一想〗你会列式吗?
列出的算式:(3×108)×(5×102)
=(3×5)×(108×102)
你会计算吗? 108×102=
温 故
a
n
指数
幂
底数
=a·a····a
n个a
1.“幂”的意义
2.“幂”的结构
做一做
108×102= ?
108× 102
=(10×···× 10 )×( 10×10 )
8个10
= 10×10×···×10
10个10
=1010
(乘方的意义)
(乘法的结合律)
(乘方的意义)
(1)25×22=2 ( )
=(2×2×2×2×2)
×(2×2)
=2×2×2×2×2×2×2
=27
(2)a3·a2=a( )
=(a﹒a﹒a) (a﹒a)
=a﹒a﹒a﹒a﹒a
=a5
7
5
(3)5m× 5n =5( )
=(5×5×5×…×5)
m个5
×(5×5×5 ×…×5)
n个5
=5×5×…×5
(m+n)个5
=5m+n
猜一猜
am · an =a( )
m+n
m+n
(1)25×22=2 ( )
(2)a3·a2=a( )
7
5
猜想:am · an= am+n (m、n都是正整数)
am · an =
m个a
n个a
(aa···a)
= aa···a
=am+n
(m+n)个a
即
am · an = am+n (m、n都是正整数)
(aa···a)
(乘方的意义)
(乘法结合律)
(乘方的意义)
·
知 新
证 明
观 察: am · an = am+n (m、n是正整数)
等式左边是什么运算?有什么特征?
同底数幂的乘法
相同, 是正整数
等式右边是怎样体现同底数幂乘法性质的?
底数不变,指数相加
条件:①乘法
②同底数幂
结果:①底数不变
②指数相加
底数 指数
底数 指数
am · an = am+n (m、n都是正整数)
同底数幂相乘,底数不变,指数相加.
同底数幂的乘法的性质:
符号语言
文字语言
我们在“知新”的路上体会到:“特殊 一般”的心路历程
我们可以直接利用它进行计算.
运 用
范 例
例1 计算:
(1)x2 · x5 ;
(2)a · a6;
解: (1)x2 · x5= x2+5 =x7
a=a1
(1)b3·b3=2b3 (2)b3+b3=b6 (3)(-x)4·(-x)4=(-x)16 (4)n3·n7=n10 (5)a2+a5=a7 (6)y5·y4=y20 (7)x·x2=x2 (8)b4·b4=2b4
辨一辨
判断正误(拿出你们的答题器,开始你们的作答)
算一算
(1) 108×102
(2) x5·x5
(3)-a3·(-a)6
(4) (-2)8 ×(-2)7
(5) xm · x3m+1
(6) a · a6 · a3
= a7 · a3 =a10
例如:
我们在“运用”的路上体会到:“一般 特殊”的思考方式的心路历程
am· an· ap = am+n+p (m、n、p都是正整数)
am·an·ap
=(a·a· … ·a)(a·a· … ·a)(a·a· … ·a)
n个a
m个a
p个a
=am+n+p
猜 想
证 明
推论一
这一性质可以推广到多个同底数幂相乘的情况:
am· an· ap = am+n+p (m、n、p都是正整数)
结 论
(m,n……p都是正整数).
am+n = am·an
(a·a· … ·a)(a·a· … ·a)
m个a
n个a
= am·an=右边
证 明
反过来想一想:当m、n都是正整数时,则am+n = am · an对吗?
推论二
am+n = am · an (m、n都是正整数)
结 论
( m+n)个a
左边=am+n =(a·a· … ·a)
=
这些拓展,在今后的数学学习中运用是很广泛的,你会了吗?
1.若x·xm·x4=x7,则m=____.
试一试
2.填一填:若xm =3 ,xn =2,那么,
(1)xm+n = × = × = ;
(2)x2m = × = × = ;
(3)x2m+n = × = × = .
xm
xn
6
3
2
xm
xm
3
3
9
x2m
xn
9
2
18
实际上,关于同底数幂的运算还有许多的拓展呢。比如:
3.计算:
4.计算: (m是正整数)
A
A
今天我们学了什么?
今天我们悟到什么?
今天的质疑和发现?
升 华
特殊
一般
特殊
例子
应用
公式
拓展思维的宽度,深华思考的层次是成为一代“学霸”的路径.
延 续
巩固性作业(必做)
(1)计算
①c·c11; ②104×102×10; ③(-b)3·(-b)2;
④-b3·b2; ⑤xm-1·xm+1(m>1); ⑥a·a3·an.
(2)已知am=2,an=8,求am+n.
延 续
拓展性作业(希望做)
(1)已知:am=2, an=3, 求a m+n的值。
(2)如果an-2an+1=a11,求n的值。
(3)3×27×9 =3x,求x的值。
(4)已知:a2 ·a6 = 28, 求a的值。
(6)如果xm-n·x2n+1= xn,且ym-1·y4-n= y7,
求m和n的值。
延 续
放飞性作业(鼓励做)
研究性作业 (小组合作完成):请收集有关同底数幂乘法的精彩中考题
阅读性作业(至少读一本):在第十四章“整式的乘法与因式分解”阶段的学习期间,
推荐如下参考书目:
1. 《乘法公式的乾坤大挪移》(储平)(上海科技出版社)
2. 《因式分解技巧》(单 墫)(华东师范大学出版社)
谢谢聆听
