北师大版九年级数学上册 4.2平行线分线段成比例 教案
文档属性
| 名称 | 北师大版九年级数学上册 4.2平行线分线段成比例 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 231.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-13 00:00:00 | ||
图片预览


文档简介
第四章 图形的相似
2 平行线分线段成比例
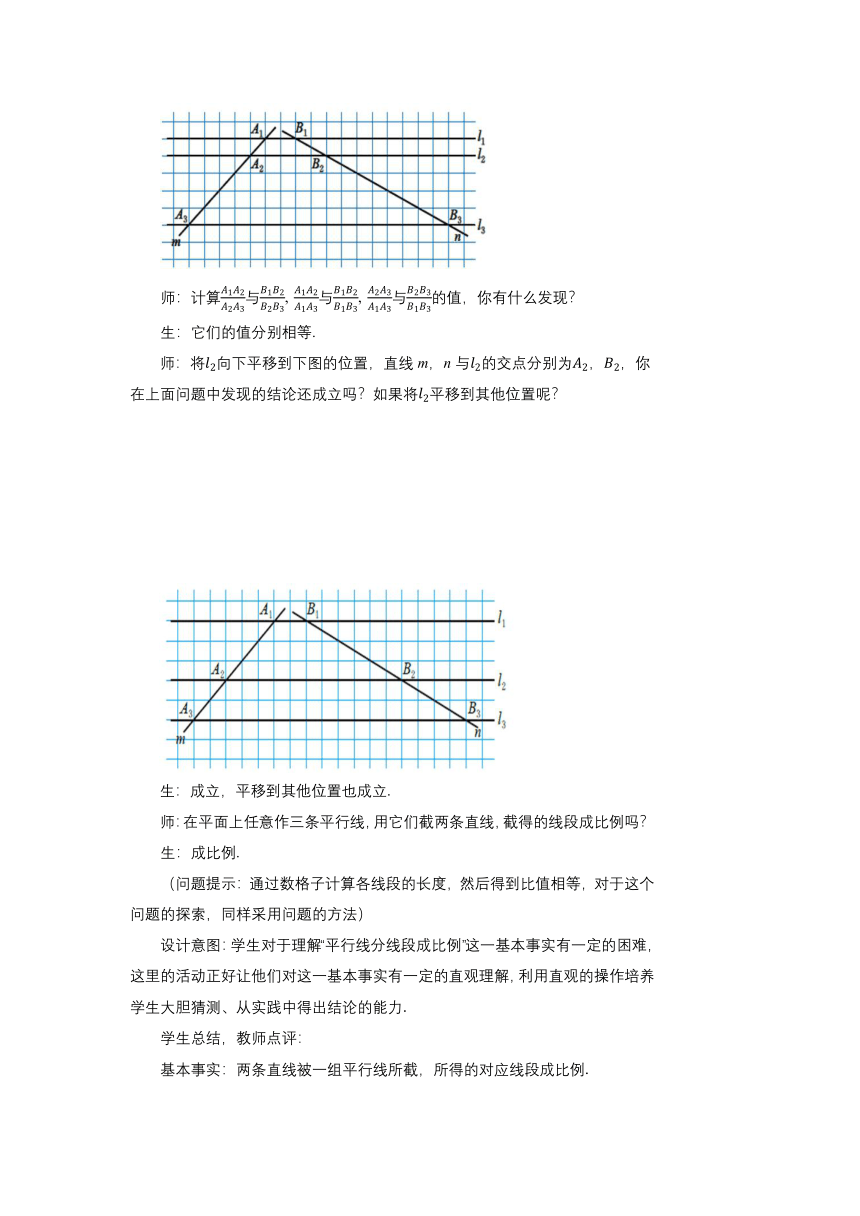
教学目标 1.理解平行线分线段成比例基本事实及其推论,初步熟悉平行线分线段成比例定理的应用. 2.通过探索过程培养学生观察、分析、概括能力,了解特殊与一般的辩证关系. 3.有关比例的计算,让学生懂得数学在现实生活中的作用,增强学生学好数学的信心. 教学重难点 重点:平行线分线段成比例定理、推论及其应用. 难点:会用平行线分线段成比例的事实和推论解决相关的计算和证明问题. 教学过程 导入新课 教师提问 1.比例线段的概念. 2.比例的基本性质. 3.比例的等比性质. 4.比例的合比性质. 让学生逐一回答,然后教师给予肯定和鼓励. 由这一问题来引入本节课要研究的课题. 设计意图:让学生通过对比例线段及比的性质的回顾,能够加深对以前知识的印象,更能够为这节课知识的学习奠定基础. 探究新知 一、预习新知 如图,小方格的边长均为1,直线,分别交直线m,n于点,. 师:计算与,与,与的值,你有什么发现? 生:它们的值分别相等. 师:将向下平移到下图的位置,直线m,n与的交点分别为,,你在上面问题中发现的结论还成立吗?如果将平移到其他位置呢? 生:成立,平移到其他位置也成立. 师:在平面上任意作三条平行线,用它们截两条直线,截得的线段成比例吗? 生:成比例. (问题提示:通过数格子计算各线段的长度,然后得到比值相等,对于这个问题的探索,同样采用问题的方法) 设计意图:学生对于理解“平行线分线段成比例”这一基本事实有一定的困难,这里的活动正好让他们对这一基本事实有一定的直观理解,利用直观的操作培养学生大胆猜测、从实践中得出结论的能力. 学生总结,教师点评: 基本事实:两条直线被一组平行线所截,所得的对应线段成比例. 知识拓展:(1)理解“对应”的含义:对应线段成比例是指所得的对应位置的线段成比例,如,,,. (2)平行线分线段成比例定理与平行直线和被截两直线的交点位置无关. 巩固练习 如图,已知l1∥l2∥l3,下列比例式错误的是( ) A. B. C. D. 答案:C 二、合作探究 多媒体展示教材中图4-8和图4-9,直线a ∥b∥ c ,分别交直线m,n于 A1,A2,A3,B1,B2,B3 ,过点A1作直线n的平行线,分别交直线b,c于点C2,C3,图4-9中有哪些成比例线段? 提示:此题没有给出方格,让学生脱离方格,不计算,运用平行四边形的性质定理得出结论. 让学生独立完成,然后小组讨论,找小组代表发表本组的见解,教师给予纠正及鼓励. 学生总结,教师点评: 推论:平行于三角形一边的直线与其他两边相交,截得的对应线段成比例. 设计意图:学生已经学习过特殊平行四边形的性质与证明,所以很容易得出A1C2=B1B2,C2C3=B2B3,进而得出结论,而且让学生归纳表述结论,可培养学生的抽象概括能力及语言表达能力. 典型例题 【例1】如图,DE∥FG∥BC,AD∶DF∶FB=2∶3∶4,如果EG=4,则AC的长为多少? 【问题探索】根据平行线分线段成比例定理列出比例式,分别求出AE,GC的长,计算即可. 【解】∵DE∥FG∥BC, ∴AE∶EG∶GC=AD∶DF∶FB=2∶3∶4. ∵EG=4, ∴AE==,GC==, ∴AC=AE+EG+GC=12. 【总结】平行于三角形一边的直线与其他两边相交,截得的对应线段成比例,这是平行线分线段成比例的推论.平行线分线段成比例的推论是在平行线分线段成比例的基础上得到的,是通过作辅助线构造平行四边形,并利用了平行四边形对边相等的性质证得的. 【例2】已知,AD是△ABC的中线,点E在AC上,BE交AD于点F.某数学兴趣小组在研究这个图形时得到如下结论: (1)当=时,=; (2)当=时,=; (3)当=时,=; … 猜想:当=时,=?并说明理由. 【问题探索】要求当=时,的值为多少,我们可以通过作辅助线,利用平行线分线段成比例定理,证得==,得到EG=nAE,证明EG=CG,AC=(2n+1)AE,即可解决问题. 【解】猜想:当=时,=.理由如下: 如图,过点D作DG∥BE,交AC于点G, 则==, ∴ =,EG=nAE. ∵ AD是△ABC的中线,∴ 点D是BC的中点. 又∵ DG∥BE, ∴ EG=CG,AC=(2n+1)AE, ∴ =. 【总结】通过作平行线,利用平行线分线段成比例的基本事实证明三角形中线段的比例,解题的关键是作辅助线,构造平行线,灵活运用平行线分线段成比例定理来分析、判断、推理或解答. 课堂练习 1.如图,已知l1∥l2∥l3,AC=4,,CE=6,BD=3,则DF=( ) A.2 B.4.5 C.6 D.8 2.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC.已知AE=6,,则EC=( ) A.4.5 B.8 C.10.5 D.14 3. 如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若=,DE=4,则EF的长是______. 4.如图,在△ABC中,DE//BC,EF//AB,AD=2,BD=4,BC=8.求BF和CF的长. 参考答案 1.B 2.B 3.6 4.解:∵ AD=2,BD=4,∴ AB=6. ∵ DE//BC, ∴ . ∵ EF//AB,∴ ,∴ ,∴ BF=. ∴ CF=8-=. 课堂小结 (学生总结,老师点评) 1.平行线分线段成比例定理 2.平行线分线段成比例推论 3.“A”字型基本图形和“X”字型基本图形 布置作业 习题4.3第2题、第3题 板书设计 第四章 图形的相似 2 平行线分线段成比例 平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例. 推论:平行于三角形一边的直线与其他两边相交,截得的对应线段成比例.
2 平行线分线段成比例
教学目标 1.理解平行线分线段成比例基本事实及其推论,初步熟悉平行线分线段成比例定理的应用. 2.通过探索过程培养学生观察、分析、概括能力,了解特殊与一般的辩证关系. 3.有关比例的计算,让学生懂得数学在现实生活中的作用,增强学生学好数学的信心. 教学重难点 重点:平行线分线段成比例定理、推论及其应用. 难点:会用平行线分线段成比例的事实和推论解决相关的计算和证明问题. 教学过程 导入新课 教师提问 1.比例线段的概念. 2.比例的基本性质. 3.比例的等比性质. 4.比例的合比性质. 让学生逐一回答,然后教师给予肯定和鼓励. 由这一问题来引入本节课要研究的课题. 设计意图:让学生通过对比例线段及比的性质的回顾,能够加深对以前知识的印象,更能够为这节课知识的学习奠定基础. 探究新知 一、预习新知 如图,小方格的边长均为1,直线,分别交直线m,n于点,. 师:计算与,与,与的值,你有什么发现? 生:它们的值分别相等. 师:将向下平移到下图的位置,直线m,n与的交点分别为,,你在上面问题中发现的结论还成立吗?如果将平移到其他位置呢? 生:成立,平移到其他位置也成立. 师:在平面上任意作三条平行线,用它们截两条直线,截得的线段成比例吗? 生:成比例. (问题提示:通过数格子计算各线段的长度,然后得到比值相等,对于这个问题的探索,同样采用问题的方法) 设计意图:学生对于理解“平行线分线段成比例”这一基本事实有一定的困难,这里的活动正好让他们对这一基本事实有一定的直观理解,利用直观的操作培养学生大胆猜测、从实践中得出结论的能力. 学生总结,教师点评: 基本事实:两条直线被一组平行线所截,所得的对应线段成比例. 知识拓展:(1)理解“对应”的含义:对应线段成比例是指所得的对应位置的线段成比例,如,,,. (2)平行线分线段成比例定理与平行直线和被截两直线的交点位置无关. 巩固练习 如图,已知l1∥l2∥l3,下列比例式错误的是( ) A. B. C. D. 答案:C 二、合作探究 多媒体展示教材中图4-8和图4-9,直线a ∥b∥ c ,分别交直线m,n于 A1,A2,A3,B1,B2,B3 ,过点A1作直线n的平行线,分别交直线b,c于点C2,C3,图4-9中有哪些成比例线段? 提示:此题没有给出方格,让学生脱离方格,不计算,运用平行四边形的性质定理得出结论. 让学生独立完成,然后小组讨论,找小组代表发表本组的见解,教师给予纠正及鼓励. 学生总结,教师点评: 推论:平行于三角形一边的直线与其他两边相交,截得的对应线段成比例. 设计意图:学生已经学习过特殊平行四边形的性质与证明,所以很容易得出A1C2=B1B2,C2C3=B2B3,进而得出结论,而且让学生归纳表述结论,可培养学生的抽象概括能力及语言表达能力. 典型例题 【例1】如图,DE∥FG∥BC,AD∶DF∶FB=2∶3∶4,如果EG=4,则AC的长为多少? 【问题探索】根据平行线分线段成比例定理列出比例式,分别求出AE,GC的长,计算即可. 【解】∵DE∥FG∥BC, ∴AE∶EG∶GC=AD∶DF∶FB=2∶3∶4. ∵EG=4, ∴AE==,GC==, ∴AC=AE+EG+GC=12. 【总结】平行于三角形一边的直线与其他两边相交,截得的对应线段成比例,这是平行线分线段成比例的推论.平行线分线段成比例的推论是在平行线分线段成比例的基础上得到的,是通过作辅助线构造平行四边形,并利用了平行四边形对边相等的性质证得的. 【例2】已知,AD是△ABC的中线,点E在AC上,BE交AD于点F.某数学兴趣小组在研究这个图形时得到如下结论: (1)当=时,=; (2)当=时,=; (3)当=时,=; … 猜想:当=时,=?并说明理由. 【问题探索】要求当=时,的值为多少,我们可以通过作辅助线,利用平行线分线段成比例定理,证得==,得到EG=nAE,证明EG=CG,AC=(2n+1)AE,即可解决问题. 【解】猜想:当=时,=.理由如下: 如图,过点D作DG∥BE,交AC于点G, 则==, ∴ =,EG=nAE. ∵ AD是△ABC的中线,∴ 点D是BC的中点. 又∵ DG∥BE, ∴ EG=CG,AC=(2n+1)AE, ∴ =. 【总结】通过作平行线,利用平行线分线段成比例的基本事实证明三角形中线段的比例,解题的关键是作辅助线,构造平行线,灵活运用平行线分线段成比例定理来分析、判断、推理或解答. 课堂练习 1.如图,已知l1∥l2∥l3,AC=4,,CE=6,BD=3,则DF=( ) A.2 B.4.5 C.6 D.8 2.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC.已知AE=6,,则EC=( ) A.4.5 B.8 C.10.5 D.14 3. 如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若=,DE=4,则EF的长是______. 4.如图,在△ABC中,DE//BC,EF//AB,AD=2,BD=4,BC=8.求BF和CF的长. 参考答案 1.B 2.B 3.6 4.解:∵ AD=2,BD=4,∴ AB=6. ∵ DE//BC, ∴ . ∵ EF//AB,∴ ,∴ ,∴ BF=. ∴ CF=8-=. 课堂小结 (学生总结,老师点评) 1.平行线分线段成比例定理 2.平行线分线段成比例推论 3.“A”字型基本图形和“X”字型基本图形 布置作业 习题4.3第2题、第3题 板书设计 第四章 图形的相似 2 平行线分线段成比例 平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例. 推论:平行于三角形一边的直线与其他两边相交,截得的对应线段成比例.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
