人教版九年级上册24.1.4圆周角 (第二课时) 课件(共19张PPT)
文档属性
| 名称 | 人教版九年级上册24.1.4圆周角 (第二课时) 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 553.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-14 09:47:03 | ||
图片预览





文档简介
(共19张PPT)
第二十四章 圆
24.1.4 圆周角
(第二课时)
人教版 九年级上册
学习目标
1.掌握圆周角的定理的内容及简单应用;
2.掌握圆周角的定理的三个推论及简单应用;
3.理解圆内接多边形定义;
4.掌握圆内接四边形的性质.
说一说下列图形名称,写的时候应该注意什么
四边形ABCD
△ABC
五边形ABCDE
六边形ABCDEF
写的时候应该注意按顺时针或逆时针顺序
知识回顾
观察下列图形与圆的位置关系
情境导入
多边形的顶点都在圆上
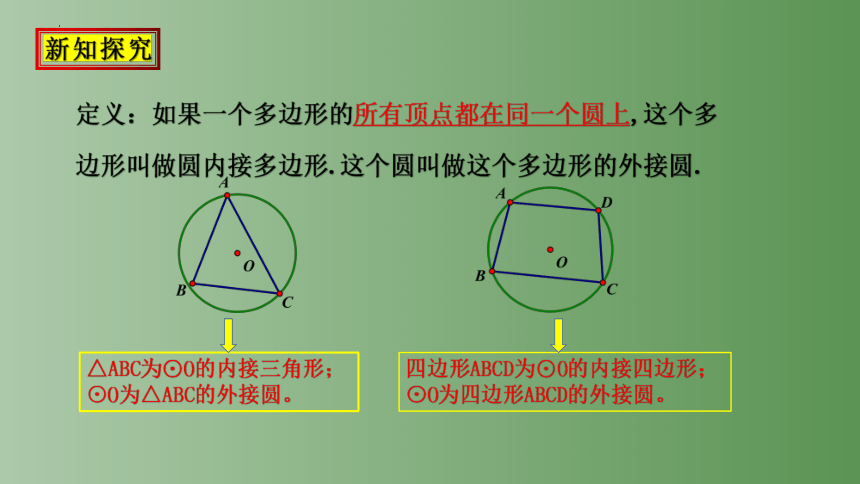
定义:如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形.这个圆叫做这个多边形的外接圆.
新知探究
四边形ABCD为⊙O的内接四边形;⊙O为四边形ABCD的外接圆。
△ABC为⊙O的内接三角形;⊙O为△ABC的外接圆。
新知探究
如图,四边形ABCD内接于⊙O,猜想∠A与∠C, ∠B与∠D之间的关系并证明你的猜想.
解:∠A与∠C, ∠B与∠D之间的关系为:
∠A+∠C=180 ,∠B+∠D=180
理由为:连接OB、OD
1
⌒
2
同理可证∠B+∠D=180
总结归纳
圆内接四边形对角互补.
几何语言:
∵四边形ABCD内接于⊙O
∴∠A+∠C=1800,∠B+∠D=1800
求证:圆内接四边形的任何一个外角都等于它的内对角.已知:如图,四边形 ABCD是⊙O的内接四边形.求证:∠DCE=∠A.
证明:∵∠DCE+∠BCD=180°,
又∵∠A+∠BCD=180°,∴∠DCE=∠A.
例题分析
结论:圆内接四边形的任何一个外角都等于它的内对角.
如图 ,四边形 ABCD 是圆内接四边形,点 E 是BC 延长线上一点,若∠BAD=105°,则∠DCE 的大小是( )A.115° B.105°
C.100° D.95°
B
跟踪练习
如图,⊙C经过坐标原点,且与两坐标轴分别交于点A、B,点A的坐标为(0,4),M是⊙C上一点,∠BMO=120°.(1)求证:AB为⊙C的直径;例题分析证明:∵∠AOB=90°∴AB为⊙C的直径如图,⊙C经过坐标原点,且与两坐标轴分别交于点A、B,点A的坐标为(0,4),M是⊙C上一点,∠BMO=120°.(2)求⊙C的半径及圆心C的坐标.例题分析(2)∵四边形ABMO内接于⊙C,∴∠A+∠M=1800∵∠BMO=120°,∴∠A=600∴∠ABO=300,∴AB=2AO∵AO=4,∴AB=8,⊙C的半径为4.E如图,⊙C经过坐标原点,且与两坐标轴分别交于点A、B,点A的坐标为(0,4),M是⊙C上一点,∠BMO=120°.(3)求圆心C的坐标.例题分析(3)∵过点C作CE BO,∴BE=EO∵AC=CB,∴ CE=AO=2由勾股定理得BE2=BC2-CE2∴BE=2√3,EO=2√3,∴C点坐标是(-2√3,2)E∟圆周角定理:
定理一条弧所对的圆周角等于它所对的圆心角的一半.
本课小结
推论
同弧或等弧所对的圆周角相等;
在同圆或等圆中,相等的圆周角所对的弧相等.
半圆(或直径)所对的圆周角是90°;
90°的圆周角所对的弦是直径.
圆内接四边形的性质:圆内接四边形对角互补
1.如图,点A、B、C在圆O上,BC∥OA,连接BO并延长,交圆O于点D,连接AC,DC,若∠A=28°,则∠D的大小为 .当堂检测2.如图,AB是⊙O的直径,点C,D,E都在⊙O上,∠1=54°,则∠2= °.当堂检测3.已知圆的直径为2,弦AB=,则弦AB所对的圆周角的度数是 .当堂检测
4.如图,四边形ABCD内接于⊙O,如果∠BOD=130°,则∠BCD是( )
A.115° B.130°
C.65° D.50°
5.如图,弦AB所对的圆心角为80°,则弦AB所对的圆周角的度数为 .
当堂检测
6.如图,四边形ABCD内接于⊙O,连接AC、BD,若AC=AD,∠CBE=70°,求∠DBC.
当堂检测
坚持就是胜利
第二十四章 圆
24.1.4 圆周角
(第二课时)
人教版 九年级上册
学习目标
1.掌握圆周角的定理的内容及简单应用;
2.掌握圆周角的定理的三个推论及简单应用;
3.理解圆内接多边形定义;
4.掌握圆内接四边形的性质.
说一说下列图形名称,写的时候应该注意什么
四边形ABCD
△ABC
五边形ABCDE
六边形ABCDEF
写的时候应该注意按顺时针或逆时针顺序
知识回顾
观察下列图形与圆的位置关系
情境导入
多边形的顶点都在圆上
定义:如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形.这个圆叫做这个多边形的外接圆.
新知探究
四边形ABCD为⊙O的内接四边形;⊙O为四边形ABCD的外接圆。
△ABC为⊙O的内接三角形;⊙O为△ABC的外接圆。
新知探究
如图,四边形ABCD内接于⊙O,猜想∠A与∠C, ∠B与∠D之间的关系并证明你的猜想.
解:∠A与∠C, ∠B与∠D之间的关系为:
∠A+∠C=180 ,∠B+∠D=180
理由为:连接OB、OD
1
⌒
2
同理可证∠B+∠D=180
总结归纳
圆内接四边形对角互补.
几何语言:
∵四边形ABCD内接于⊙O
∴∠A+∠C=1800,∠B+∠D=1800
求证:圆内接四边形的任何一个外角都等于它的内对角.已知:如图,四边形 ABCD是⊙O的内接四边形.求证:∠DCE=∠A.
证明:∵∠DCE+∠BCD=180°,
又∵∠A+∠BCD=180°,∴∠DCE=∠A.
例题分析
结论:圆内接四边形的任何一个外角都等于它的内对角.
如图 ,四边形 ABCD 是圆内接四边形,点 E 是BC 延长线上一点,若∠BAD=105°,则∠DCE 的大小是( )A.115° B.105°
C.100° D.95°
B
跟踪练习
如图,⊙C经过坐标原点,且与两坐标轴分别交于点A、B,点A的坐标为(0,4),M是⊙C上一点,∠BMO=120°.(1)求证:AB为⊙C的直径;例题分析证明:∵∠AOB=90°∴AB为⊙C的直径如图,⊙C经过坐标原点,且与两坐标轴分别交于点A、B,点A的坐标为(0,4),M是⊙C上一点,∠BMO=120°.(2)求⊙C的半径及圆心C的坐标.例题分析(2)∵四边形ABMO内接于⊙C,∴∠A+∠M=1800∵∠BMO=120°,∴∠A=600∴∠ABO=300,∴AB=2AO∵AO=4,∴AB=8,⊙C的半径为4.E如图,⊙C经过坐标原点,且与两坐标轴分别交于点A、B,点A的坐标为(0,4),M是⊙C上一点,∠BMO=120°.(3)求圆心C的坐标.例题分析(3)∵过点C作CE BO,∴BE=EO∵AC=CB,∴ CE=AO=2由勾股定理得BE2=BC2-CE2∴BE=2√3,EO=2√3,∴C点坐标是(-2√3,2)E∟圆周角定理:
定理一条弧所对的圆周角等于它所对的圆心角的一半.
本课小结
推论
同弧或等弧所对的圆周角相等;
在同圆或等圆中,相等的圆周角所对的弧相等.
半圆(或直径)所对的圆周角是90°;
90°的圆周角所对的弦是直径.
圆内接四边形的性质:圆内接四边形对角互补
1.如图,点A、B、C在圆O上,BC∥OA,连接BO并延长,交圆O于点D,连接AC,DC,若∠A=28°,则∠D的大小为 .当堂检测2.如图,AB是⊙O的直径,点C,D,E都在⊙O上,∠1=54°,则∠2= °.当堂检测3.已知圆的直径为2,弦AB=,则弦AB所对的圆周角的度数是 .当堂检测
4.如图,四边形ABCD内接于⊙O,如果∠BOD=130°,则∠BCD是( )
A.115° B.130°
C.65° D.50°
5.如图,弦AB所对的圆心角为80°,则弦AB所对的圆周角的度数为 .
当堂检测
6.如图,四边形ABCD内接于⊙O,连接AC、BD,若AC=AD,∠CBE=70°,求∠DBC.
当堂检测
坚持就是胜利
同课章节目录
