第六章 特殊平行四边形重点解析试卷(含解析)
文档属性
| 名称 | 第六章 特殊平行四边形重点解析试卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-19 08:42:44 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
鲁教版(五四制)八年级数学下册第六章特殊平行四边形重点解析
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的 ( http: / / www.21cnjy.com )位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。【来源:21·世纪·教育·网】
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如图,正方形纸片ABCD的四个顶点分别在四条平行线、、、上,这四条直线中相邻两条之间的距离依次为、、,若,,则正方形的面积S等于( )
( http: / / www.21cnjy.com / )
A.34 B.89 C.74 D.109
2、矩形ABCD的对角线交于点O,∠AOD=120°,AO=3,则BC的长度是( )
A.3 B. C. D.6
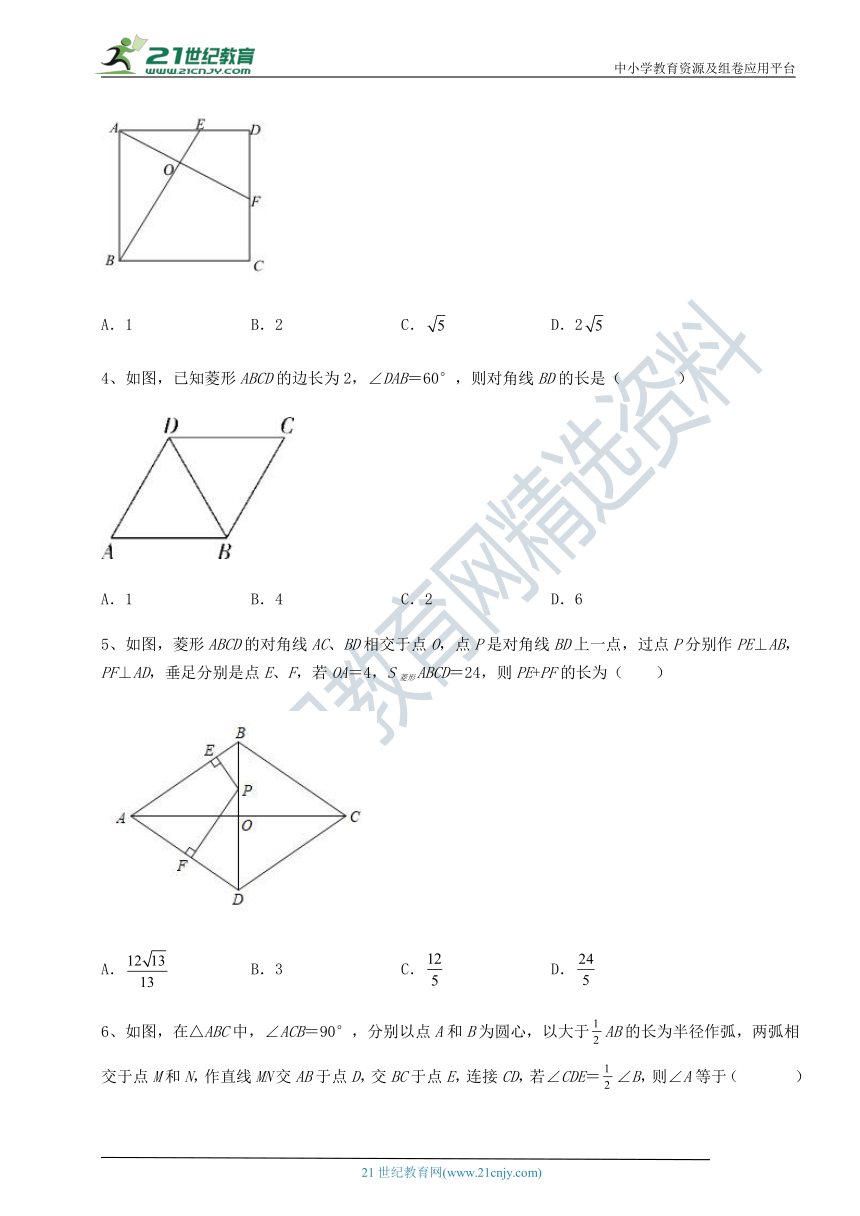
3、如图,在正方形ABCD中, ( http: / / www.21cnjy.com )点E、点F分别在AD、CD上,且AE=DF,若四边形OEDF的面积是1,OA的长为1,则正方形的边长AB为( )www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
A.1 B.2 C. D.2
4、如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是( )
( http: / / www.21cnjy.com / )
A.1 B.4 C.2 D.6
5、如图,菱形ABCD的对角线AC ( http: / / www.21cnjy.com )、BD相交于点O,点P是对角线BD上一点,过点P分别作PE⊥AB,PF⊥AD,垂足分别是点E、F,若OA=4,S菱形ABCD=24,则PE+PF的长为( )
( http: / / www.21cnjy.com / )
A. B.3 C. D.
6、如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以大于AB的长为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,若∠CDE=∠B,则∠A等于( )
( http: / / www.21cnjy.com / )
A.36° B.40° C.48° D.54°
7、如图,菱形的对角线、相交于点,,,为过点的一条直线,则图中阴影部分的面积为( )
( http: / / www.21cnjy.com / )
A.4 B.6 C.8 D.12
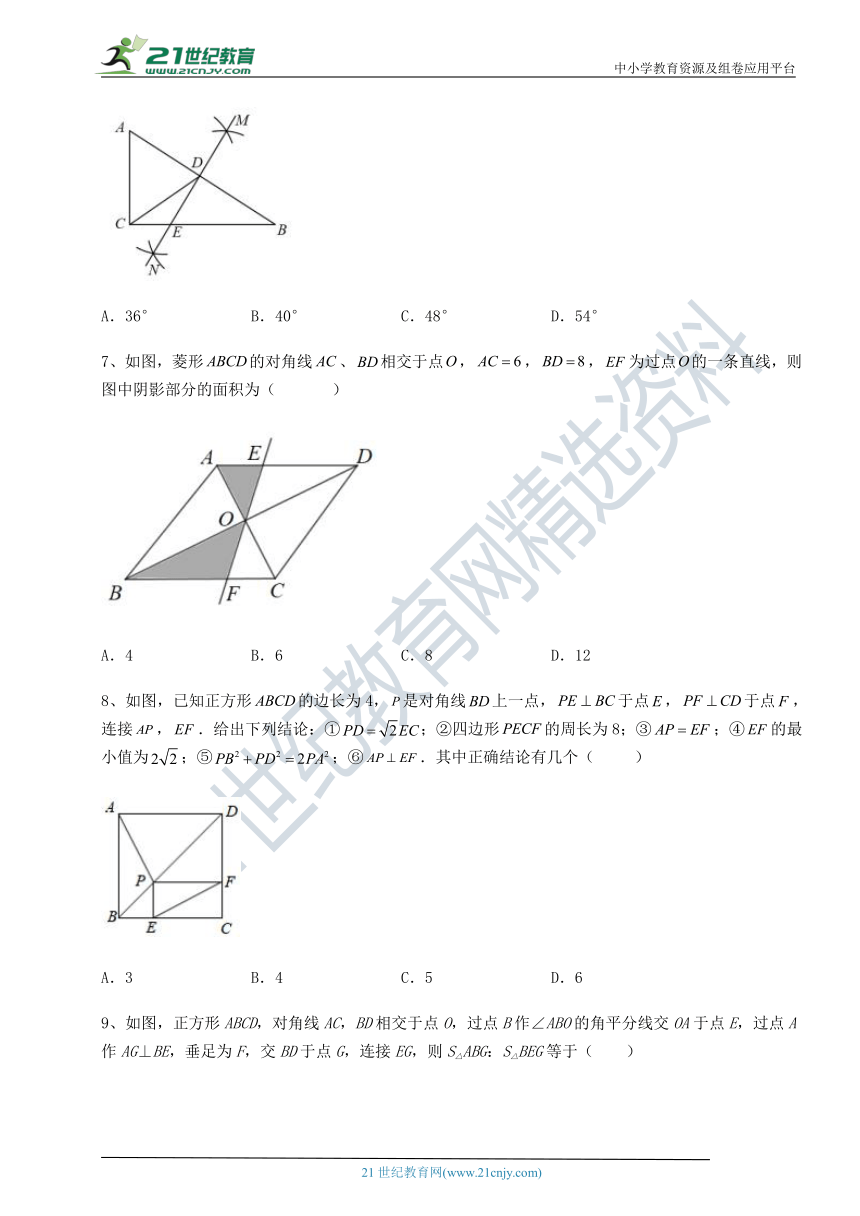
8、如图,已知正方形的边长为4,是对角线上一点,于点,于点,连接,.给出下列结论:①;②四边形的周长为8;③;④的最小值为;⑤;⑥.其中正确结论有几个( )
( http: / / www.21cnjy.com / )
A.3 B.4 C.5 D.6
9、如图,正方形ABCD,对角线AC,BD ( http: / / www.21cnjy.com )相交于点O,过点B作∠ABO的角平分线交OA于点E,过点A作AG⊥BE,垂足为F,交BD于点G,连接EG,则S△ABG:S△BEG等于( )
( http: / / www.21cnjy.com / )
A.3:5 B.:2 C.1:2 D.(+1):1
10、下列命题是真命题的有( )个.
①一组对边相等的四边形是矩形;②两 ( http: / / www.21cnjy.com )条对角线相等的四边形是矩形;③四条边都相等且对角线互相垂直的四边形是正方形;④四条边都相等的四边形是菱形;⑤一组邻边相等的矩形是正方形.
A.1 B.2 C.3 D.4
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、如图,在中,,,与分别是斜边上的高和中线,那么_______度.
( http: / / www.21cnjy.com / )
2、正方形的边长与它的对角线的长度的比值为_____.
3、如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AM的长为1.2km,则M,C两点间的距离为___km.21·世纪*教育网
( http: / / www.21cnjy.com / )
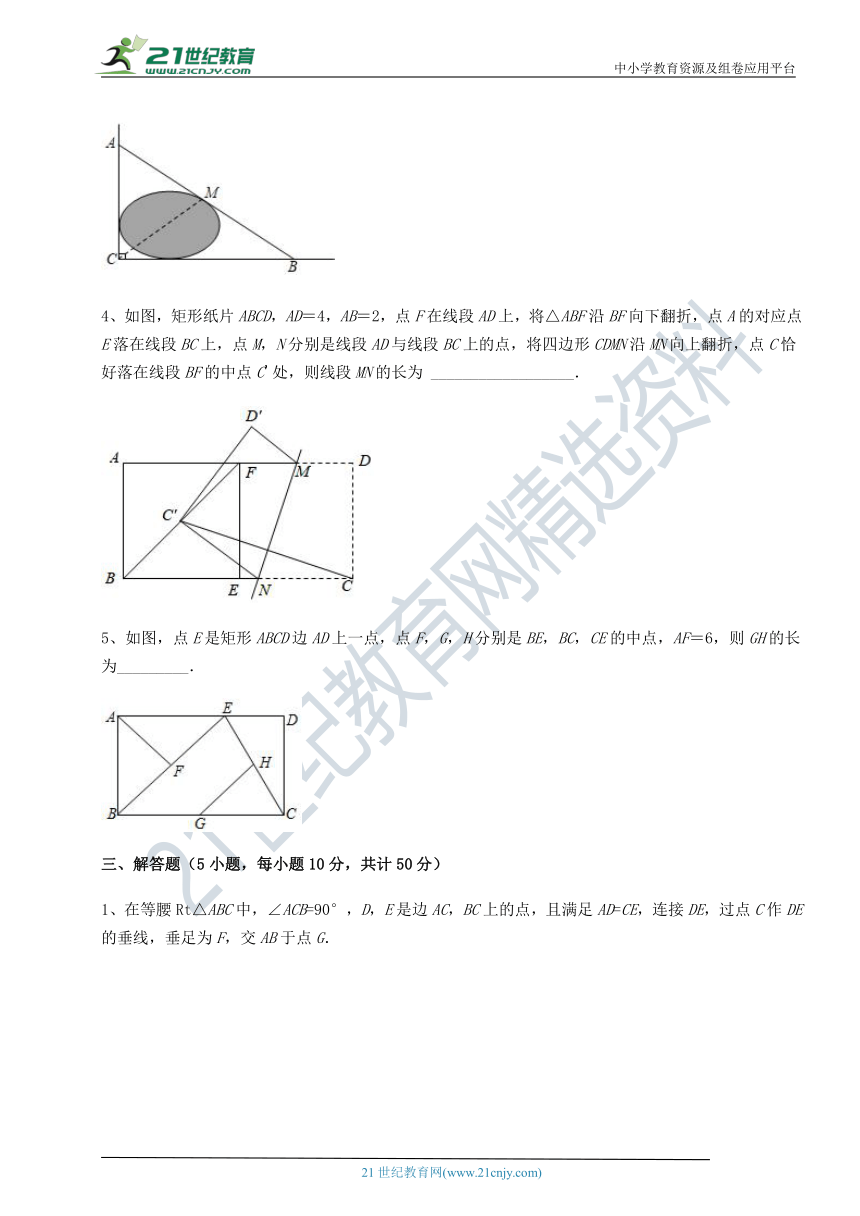
4、如图,矩形纸片ABCD, ( http: / / www.21cnjy.com )AD=4,AB=2,点F在线段AD上,将△ABF沿BF向下翻折,点A的对应点E落在线段BC上,点M,N分别是线段AD与线段BC上的点,将四边形CDMN沿MN向上翻折,点C恰好落在线段BF的中点C'处,则线段MN的长为 __________________.
( http: / / www.21cnjy.com / )
5、如图,点E是矩形ABCD边AD上一点,点F,G,H分别是BE,BC,CE的中点,AF=6,则GH的长为_________.
( http: / / www.21cnjy.com / )
三、解答题(5小题,每小题10分,共计50分)
1、在等腰Rt△ABC中,∠ACB ( http: / / www.21cnjy.com )=90°,D,E是边AC,BC上的点,且满足AD=CE,连接DE,过点C作DE的垂线,垂足为F,交AB于点G.
( http: / / www.21cnjy.com / )
(1)点D如图所示.
①请依题意在下图中补全图形;
②猜想DE与CG的数量关系,并证明;
(2)连接DG,GE,若AB=2,直接写出四边形CDGE面积的最小值.
2、已知:线段m.
求作:矩形ABCD,使矩形宽AB=m,对角线AC=m.
3、将线段绕点逆时针旋转得到线段,继续旋转得到线段,连接.
( http: / / www.21cnjy.com / )
(1)连接.
①如图①,若,则的度数为 ;
②在第二次旋转过程中,请探究的大小是否改变.若不变,求出的度数;若改变,请说明理由.
(2)如图②.以为斜边作,使得,连接,.且.试猜想线段,之间的数量关系,写出结论并给予证明.【版权所有:21教育】
4、如图,在正方形ABCD中,点E、F分别在线段BC、CD上,连接AE、AF,且BE=DF.求证:AE=AF.
( http: / / www.21cnjy.com / )
5、如图,在菱形ABCD中,点E、F分别是边CD、BC的中点
( http: / / www.21cnjy.com / )
(1)求证:四边形BDEG是平行四边形;
(2)若菱形ABCD的边长为13,对角线AC=24,求EG的长.
-参考答案-
一、单选题
1、C
2、C
【解析】
【分析】
画出图形,由条件可求得△AOB为等边三角形,则可求得AC的长,在Rt△ABC中,由勾股定理可求得BC的长.21cnjy.com
【详解】
解:如下图所示:
( http: / / www.21cnjy.com / )
∵四边形ABCD是矩形,
∴∠ABC=90°,OA=AC,OB=BD,AC=BD,
∴OA=OB,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴OA=AB=2,
∴AC=2OA=4,
∴BC2=AC2-AB2=36-9=27,
∴BC=.
故选:D.
【点睛】
本题考查了矩形的性质、等边三角形的判定与性质以及勾股定理;熟练掌握矩形的性质,证明三角形是等边三角形是解决问题的关键.21·cn·jy·com
3、C
【解析】
【分析】
根据正方形的性质得到AB=AD ( http: / / www.21cnjy.com ),∠BAE=∠ADF=90°,根据全等三角形的性质得到∠ABE=∠DAF,求得∠AOB=90°,根据三角形的面积公式得到OA=1,由勾股定理即可得到答案.www.21-cn-jy.com
【详解】
解:∵四边形ABCD是正方形,
∴AB=AD,∠BAE=∠ADF=90°,
在△ABE与△DAF中,
,
∴△ABE≌△DAF(SAS),
∴∠ABE=∠DAF,
∴∠ABE+∠BAO=∠DAF+∠BAO=90°,
∴∠AOB=90°,
∵△ABE≌△DAF,
∴S△ABE=S△DAF,
∴S△ABE-S△AOE=S△DAF-S△AOE,
即S△ABO=S四边形OEDF=1,
∵OA=1,
∴BO=2,
∴AB=,
故选:C.
【点睛】
本题考查了正方形的性质,全等三角形的判定和性质,勾股定理,证得△ABE≌△DAF是解题的关键.
4、C
【解析】
略
5、D
【解析】
【分析】
根据菱形的面积以及的长,求得的长,勾股定理求得边长,进而根据菱形的面积等于,即可求得答案.
【详解】
解:∵四边形是菱形
∴,
OA=4,S菱形ABCD=24,
即
中,
连接
( http: / / www.21cnjy.com / )
PE⊥AB,PF⊥AD,
S菱形ABCD=24,
故选D
【点睛】
本题考查了菱形的性质,勾股定理,掌握菱形的性质是解题的关键.
6、D
【解析】
【分析】
根据线段垂直平分线的性质得到∠BDE=∠ADE=90°,AD=BD,根据直角三角形斜边上的中线等于斜边的一半可得,CD=BD=AD=AB,由等边对等角可得∠B=∠DCE,∠A=∠ACD,设∠CDE=x,则∠B=∠DCE=2x,∠ADC=90°-x,∠A=45°+x,由直角三角形两锐角互余得45°+x+2x=90°,解得x值,即可求解.2·1·c·n·j·y
【详解】
解:由题意可知:MN为AB的垂直平分线,
∴∠BDE=∠ADE=90°,AD=BD,
∵∠ACB=90°,
∴CD=BD=AD=AB,
∴∠B=∠DCE,∠A=∠ACD,
设∠CDE=x,则∠B=∠DCE=2x,∠ADC=90°-x,
∴∠A=(180°-∠ADC)=45°+x,
∴∠A+∠B=45°+x+2x=90°,
解得:x=18°,
∴∠A=45°+x=54°,
故选:D.
【点睛】
此题考查了直角三角形斜边上的中线、线 ( http: / / www.21cnjy.com )段垂直平分线的性质、三角形外角的性质及等腰三角形的性质,注意垂直平分线上任意一点,到线段两端点的距离相等.【出处:21教育名师】
7、B
【解析】
【分析】
根据菱形的性质可证出,可将阴影部分面积转化为的面积,根据菱形的面积公式计算即可.
【详解】
解:四边形为菱形,
,,,
,
,
∴,
∴,
∴
故选:.
【点睛】
此题考查了菱形的性质,菱形的面积公式,全等三角形的判定,将阴影部分的面积转化为的面积为解题关键.
8、D
【解析】
【分析】
如图,过点作于点,连接,可说明四边形为矩形,,,是等腰直角三角形,;①中,可得为等腰直角三角形,进而求,由于四边形是平行四边形,,故可知;②,四边形为矩形,进而可求矩形的周长;③证明,由全等可知,进而可说明;④,当最小时,最小,即时,最小,计算即可;⑤在和中,勾股定理求得,将线段等量替换求解即可;⑥如图1,延长与交于点,证明,得,,,进而可说明.
【详解】
解:如图,过点作于点,连接,
( http: / / www.21cnjy.com / )
由题意知
∴四边形为平行四边形
∵
∴四边形为矩形
∴
∵
∴
∵
∴
∴是等腰直角三角形
∴
①∵,
∴为等腰直角三角形
∴
,
∴
∴四边形是平行四边形
∴
∴
故①正确;
②∵
∴四边形为矩形
∴四边形的周长
故②正确;
③四边形为矩形
∵在和中
∵
∴
∴
∴
故③正确;
④∵
当最小时,最小
∴当时,即时,的最小值等于
故④正确;
⑤在和中,,
∴
故⑤正确;
⑥如图1,延长与交于点
( http: / / www.21cnjy.com / )
∵在和中
∵
∴
∴
∵
∴
∴
故⑥正确;
综上,①②③④⑤⑥正确,
故选:.
【点睛】
本题考查了正方形,矩形的判定与性质,勾股定理,等腰直角三角形,三角形全等.解题的关键在于对知识的灵活综合运用.21*cnjy*com
9、D
【解析】
【分析】
由BE平分,得,根据正方形的性质得,,故,根据AAS得,故,设,进而可用含的式子表示出线段和的长,要求的比值即求和的比值,代入即可求解.
【详解】
∵BE平分,,
∴是等腰三角形,
∴,
四边形是正方形,
∴,,
∴,
∴,
在与中,
,
∴,
∴,
设,则,
∴,
∴,
∵,,
∴.
故选:D.
【点睛】
本题主要考查了正方形的性质,角平分线的定义以及全等三角形的判定与性质,解题的关键是将两个三角形的面积比转化成两条线段的比,综合性较强.21教育名师原创作品
10、B
【解析】
【分析】
根据两条对角线平分且相等的四边形是矩形,四条边都相等的四边形是菱形,如果对角线互相垂直平分且相等,那么这个四边形是正方形进行判断即可.
【详解】
解:①一组对边相等的四边形不一定是矩形,错误;
②两条对角线相等的平行四边形是矩形,错误;
③四条边都相等且对角线互相垂直的四边形是菱形,错误;
④四条边都相等的四边形是菱形,正确;
⑤一组邻边相等的矩形是正方形,正确.
故选:B.
【点睛】
此题考查考查平行四边形、矩形、菱形、正方形的判定方法,关键是根据矩形、正方形、菱形的判定解答.
二、填空题
1、50
【解析】
【分析】
根据直角三角形中线的性质及互为余角的性质计算.
【详解】
解:,为边上的高,
,
,是斜边上的中线,
,
,
的度数为.
故答案为:50.
【点睛】
本题主要考查了直角三角形中线的性质及互为余角的性质,解题的关键是掌握三角形中线的性质.
2、##
【解析】
【分析】
由正方形的性质得出,,,由勾股定理求出,即可得出正方形的边长与对角线长的比值.
【详解】
解:四边形是正方形,
( http: / / www.21cnjy.com / )
,,,
,
;
故答案为:.
【点睛】
本题考查了正方形的性质、勾股定理;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.
3、1.2
【解析】
【分析】
根据直角三角形斜边上的中线等于斜边的一半可得CM=AM=BM解答即可.
【详解】
解:∵M是公路AB的中点,
∴AM=BM,
∵AC⊥BC,
∴CM=AM=BM,
∵AM的长为1.2km,
∴M,C两点间的距离为1.2km.
故答案为:1.2.
【点睛】
本题考查了直角三角形斜边上的中线等于斜边的一半的性质,熟记性质是解题的关键.
4、
【解析】
【分析】
先判断出四边形ABEF是正方形,进而求出BF=2,得出BC'=,过点C'作C'H⊥BC于H,CC'与MN的交点记作点K,进而求出BH=1,再用勾股定理求出CC'=,进而得出CK=,再用勾股定理求出CN= ,最后用面积建立方程求出MN即可.21世纪教育网版权所有
【详解】
解:如图,
( http: / / www.21cnjy.com / )
∵四边形ABCD是矩形,
∴∠A=∠ABC=∠D=90°,CD=AB,BC=AD=4,
∵2AB=4,
∴AB=2,
∴CD=2,
∵将△ABF沿BF向下翻折,点A的对应点E落在线段BC上,
∴∠BEF=∠A=90°,AB=BE,
∴四边形ABEF是正方形,
∴BF是正方形ABEF的对角线,
∴∠EBF=45°,BF=AB=2,
∵C'是BF的中点,
∴BC'=BF=,
过点C'作C'H⊥BC于H,CC'与MN的交点记作点K,
在Rt△BHC'中,BH=C'H=BC'=1,
∴CH=BC﹣BH=3,
在Rt△CHC'中,CC'===,
由折叠知,CK=CC'=,
设CN=x,则HN=3﹣x,
∵将四边形CDMN沿MN向上翻折,
∴CC'⊥MN,C'N=CN=x,
在Rt△C'HN中,根据勾股定理得,C'H2+HN2=C'N2,
∴12+(3﹣x)2=x2,
∴x= ,
∴CN=,
连接CM,
∵S△CMN=CN CD=MN CK,
∴MN===,
故答案为.
【点睛】
此题主要考查了折叠的性质,矩形的性质,勾股定理和面积法解题,作出辅助线构造直角三角形求出CC'是解题的关键所在.【来源:21cnj*y.co*m】
5、6
【解析】
【分析】
由矩形的性质及直角三角形斜边上的中线的性质可求解BE=2AF=12,再利用三角形中位线定理可求解.
【详解】
解:在矩形ABCD中,∠BAD=90°,
∵F为BE的中点,AF=6,
∴BE=2AF=12.
∵G,H分别为BC,EC的中点,
∴GH=BE=6,
故答案为6.
【点睛】
根据直角三角形斜边上的中线等于斜边的一半,求解BE的长是解题的关键.再根据中位线定理求出GH.
三、解答题
1、 (1)①作图见解析;②DE=CG,证明见解析;
(2)
【解析】
【分析】
(1)①按照题意作图即可; ( http: / / www.21cnjy.com )②如图1过点D作DH⊥AC交AB于H,连接CH交DE于O,连接EH,∠A=∠B=45°,∠ADH=90°,∠A=∠DHA=45°,DA=DH= CE,四边形DHEC是平行四边形,∠DCE=90°,四边形DHEC是矩形,矩形对角线相等且互相平分可知,DE=CH,OD=OC,∠ODC=∠OCD,证明∠CDE=∠BCG=∠ACH,△ACH≌△BCG,进而可说明DE=CG.2-1-c-n-j-y
(2)如图2,由(1)可知DE=CG,CG⊥DE,S四边形CDGE DE CG CG2;可知面积最小即CG的值最短;根据垂线段最短可知,当CG⊥AB时,CG的值最短,由AG=GB,∠ACB=90°,可知CGAB=1,进而可求四边形面积的最小值.21*cnjy*com
(1)
解:①图形如图1所示.
②结论:DE=CG.
证明:如图1中,过点D作DH⊥AC交AB于H,连接CH交DE于O,连接EH.
( http: / / www.21cnjy.com / )
∵AC=BC,∠ACB=90°
∴∠A=∠B=45°
∵AD⊥DH
∴∠ADH=90°
∴∠A=∠DHA=45°
∴DA=DH
∵AD=CE
∴DH=CE
∵∠ADH=∠ACB=90°
∴DH∥BC
∴四边形DHEC是平行四边形
∵∠DCE=90°
∴四边形DHEC是矩形
∴DE=CH,OD=OC=OE=OH
∴∠ODC=∠OCD
∵CG⊥DE
∴∠CDE+∠DCG=90°,∠DCG+∠BCG=90°
∴∠CDE=∠BCG=∠ACH
在△ACH和△BCG中
∵
∴△ACH≌△BCG(ASA)
∴CH=CG
∴DE=CG.
(2)
解:如图2
( http: / / www.21cnjy.com / )
由(1)可知DE=CG,CG⊥DE
∴S四边形CDGE DE CG CG2
根据垂线段最短可知,当CG⊥AB时,CG的值最短
∵CA=CB,CG⊥AB
∴AG=GB
∴CGAB=1
∴四边形CDGE的面积的最小值为.
【点睛】
本题考查了垂线段,矩形的判定与性质,三角形全等,等腰三角形的判定与性质.解题的关键在于对知识的灵活综合运用.
2、见详解
【解析】
【分析】
先作m的垂直平分线,取m ( http: / / www.21cnjy.com )的一半为AB,然后以点A为圆心,以m长为半径画弧,交m的垂直平分线于C,连结AC,利用作一个角等于已知角,过A作BC的平行线AD,过C作AB的平行线CD,两线交于D即可.
【详解】
解:先作m的垂直平分线,取m的一半为AB,
以点A为圆心,以m长为半径画弧,交m的垂直平分线于C,连结AC,
过A作BC的平行线,与过C作AB的平行线交于D,
则四边形ABCD为所求作矩形;
( http: / / www.21cnjy.com / )
∵AD∥BC,CD∥AB,
∴四边形ABCD为平行四边形,
∵BC⊥AB,
∴∠ABC=90°,
∴四边形ABCD为矩形,
∵AB=,AC=m,
∴矩形的宽与对角线满足条件,
∴四边形ABCD为所求作矩形.
【点睛】
本题考查矩形作图,线段垂直平分线,作线段等于已知线段,平行线作法,掌握矩形作图,线段垂直平分线,作线段等于已知线段,平行线作法是解题关键.
3、 (1)①30°,②不变,30°
(2),见解析
【解析】
【分析】
(1)①先推出∠ADC=50°,在推出∠ADB=20°,从而得出结果;②同理①由AC=AD推出∠ADC=90° ,由AB=AD推出∠ADB=60° ,进而推出结果;
(2)作AF⊥CD于F,推出△ABE≌△ACF,进而得出△AEF是等边三角形,再推出△ABE是等腰直角三角形,进而得出关系.
(1)
解:①,
,
,
,
,
故答案是;
②不变,理由如下:
,
,
,
,
,
(2)
,理由如下:
如图,作于,
( http: / / www.21cnjy.com / )
,
,
,
,
,
,,,
,
,,,
即,
是等边三角形,
,
,
是等腰直角三角形,
,
是等腰直角三角形,
.
【点睛】
本题考查了旋转性质,等边三角形 ( http: / / www.21cnjy.com )性质,等腰直角三角形性质,直角三角形性质,全等三角形判定和性质等知识,解决问题的关键是找出题目中线段间的关系.
4、见解析.
【解析】
【分析】
利用正方形的性质可证明△ABE≌△ADF,可得AE=AF.
【详解】
证明:∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=90°,
∵BE=DF,
在Rt△ABE与Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(SAS),
∴AE=AF.
【点睛】
本题考查了正方形的性质,全等三角形的性质与判定,掌握正方形的性质是解题的关键.
5、 (1)证明见解析
(2)10
【解析】
【分析】
(1)利用AC平分∠BAD,AB∥CD, ( http: / / www.21cnjy.com )得到∠DAC=∠DCA,即可得到AD=DC,利用一组对边平行且相等可证明四边形ABCD是平行四边形,再结合AB=AD,即可求证结论;
(2)根据菱形的性质,得到CD=13,AO ( http: / / www.21cnjy.com )=CO=12,结合中位线性质,可得四边形BDEG是平行四边形,利用勾股定理即可得到OB、OD的长度,即可求解.
(1)
证明:∵AC平分∠BAD,AB∥CD,
∴∠DAC=∠BAC,∠DCA=∠BAC,
∴∠DAC=∠DCA,
∴AD=DC,
又∵AB∥CD,AB=AD,
∴AB∥CD且AB=CD,
∴四边形ABCD是平行四边形,
∵AB=AD,
∴四边形ABCD是菱形.
(2)
解:连接BD,交AC于点O,如图:
( http: / / www.21cnjy.com / )
∵菱形ABCD的边长为13,对角线AC=24,
∴CD=13,AO=CO=12,
∵点E、F分别是边CD、BC的中点,
∴EF∥BD(中位线),
∵AC、BD是菱形的对角线,
∴AC⊥BD,OB=OD,
又∵AB∥CD,EF∥BD,
∴DE∥BG,BD∥EG,
∵四边形BDEG是平行四边形,
∴BD=EG,
在△COD中,
∵OC⊥OD,CD=13,CO=12,
∴,
∴EG=BD=10.
【点睛】
本题考查了平行四边形性质判定方法、菱形的判 ( http: / / www.21cnjy.com )定和性质、等腰三角形性质、勾股定理等知识,关键在于熟悉四边形的判定方法和在题目中找到合适的判定条件.21教育网
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
鲁教版(五四制)八年级数学下册第六章特殊平行四边形重点解析
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的 ( http: / / www.21cnjy.com )位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。【来源:21·世纪·教育·网】
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如图,正方形纸片ABCD的四个顶点分别在四条平行线、、、上,这四条直线中相邻两条之间的距离依次为、、,若,,则正方形的面积S等于( )
( http: / / www.21cnjy.com / )
A.34 B.89 C.74 D.109
2、矩形ABCD的对角线交于点O,∠AOD=120°,AO=3,则BC的长度是( )
A.3 B. C. D.6
3、如图,在正方形ABCD中, ( http: / / www.21cnjy.com )点E、点F分别在AD、CD上,且AE=DF,若四边形OEDF的面积是1,OA的长为1,则正方形的边长AB为( )www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
A.1 B.2 C. D.2
4、如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是( )
( http: / / www.21cnjy.com / )
A.1 B.4 C.2 D.6
5、如图,菱形ABCD的对角线AC ( http: / / www.21cnjy.com )、BD相交于点O,点P是对角线BD上一点,过点P分别作PE⊥AB,PF⊥AD,垂足分别是点E、F,若OA=4,S菱形ABCD=24,则PE+PF的长为( )
( http: / / www.21cnjy.com / )
A. B.3 C. D.
6、如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以大于AB的长为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,若∠CDE=∠B,则∠A等于( )
( http: / / www.21cnjy.com / )
A.36° B.40° C.48° D.54°
7、如图,菱形的对角线、相交于点,,,为过点的一条直线,则图中阴影部分的面积为( )
( http: / / www.21cnjy.com / )
A.4 B.6 C.8 D.12
8、如图,已知正方形的边长为4,是对角线上一点,于点,于点,连接,.给出下列结论:①;②四边形的周长为8;③;④的最小值为;⑤;⑥.其中正确结论有几个( )
( http: / / www.21cnjy.com / )
A.3 B.4 C.5 D.6
9、如图,正方形ABCD,对角线AC,BD ( http: / / www.21cnjy.com )相交于点O,过点B作∠ABO的角平分线交OA于点E,过点A作AG⊥BE,垂足为F,交BD于点G,连接EG,则S△ABG:S△BEG等于( )
( http: / / www.21cnjy.com / )
A.3:5 B.:2 C.1:2 D.(+1):1
10、下列命题是真命题的有( )个.
①一组对边相等的四边形是矩形;②两 ( http: / / www.21cnjy.com )条对角线相等的四边形是矩形;③四条边都相等且对角线互相垂直的四边形是正方形;④四条边都相等的四边形是菱形;⑤一组邻边相等的矩形是正方形.
A.1 B.2 C.3 D.4
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、如图,在中,,,与分别是斜边上的高和中线,那么_______度.
( http: / / www.21cnjy.com / )
2、正方形的边长与它的对角线的长度的比值为_____.
3、如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AM的长为1.2km,则M,C两点间的距离为___km.21·世纪*教育网
( http: / / www.21cnjy.com / )
4、如图,矩形纸片ABCD, ( http: / / www.21cnjy.com )AD=4,AB=2,点F在线段AD上,将△ABF沿BF向下翻折,点A的对应点E落在线段BC上,点M,N分别是线段AD与线段BC上的点,将四边形CDMN沿MN向上翻折,点C恰好落在线段BF的中点C'处,则线段MN的长为 __________________.
( http: / / www.21cnjy.com / )
5、如图,点E是矩形ABCD边AD上一点,点F,G,H分别是BE,BC,CE的中点,AF=6,则GH的长为_________.
( http: / / www.21cnjy.com / )
三、解答题(5小题,每小题10分,共计50分)
1、在等腰Rt△ABC中,∠ACB ( http: / / www.21cnjy.com )=90°,D,E是边AC,BC上的点,且满足AD=CE,连接DE,过点C作DE的垂线,垂足为F,交AB于点G.
( http: / / www.21cnjy.com / )
(1)点D如图所示.
①请依题意在下图中补全图形;
②猜想DE与CG的数量关系,并证明;
(2)连接DG,GE,若AB=2,直接写出四边形CDGE面积的最小值.
2、已知:线段m.
求作:矩形ABCD,使矩形宽AB=m,对角线AC=m.
3、将线段绕点逆时针旋转得到线段,继续旋转得到线段,连接.
( http: / / www.21cnjy.com / )
(1)连接.
①如图①,若,则的度数为 ;
②在第二次旋转过程中,请探究的大小是否改变.若不变,求出的度数;若改变,请说明理由.
(2)如图②.以为斜边作,使得,连接,.且.试猜想线段,之间的数量关系,写出结论并给予证明.【版权所有:21教育】
4、如图,在正方形ABCD中,点E、F分别在线段BC、CD上,连接AE、AF,且BE=DF.求证:AE=AF.
( http: / / www.21cnjy.com / )
5、如图,在菱形ABCD中,点E、F分别是边CD、BC的中点
( http: / / www.21cnjy.com / )
(1)求证:四边形BDEG是平行四边形;
(2)若菱形ABCD的边长为13,对角线AC=24,求EG的长.
-参考答案-
一、单选题
1、C
2、C
【解析】
【分析】
画出图形,由条件可求得△AOB为等边三角形,则可求得AC的长,在Rt△ABC中,由勾股定理可求得BC的长.21cnjy.com
【详解】
解:如下图所示:
( http: / / www.21cnjy.com / )
∵四边形ABCD是矩形,
∴∠ABC=90°,OA=AC,OB=BD,AC=BD,
∴OA=OB,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴OA=AB=2,
∴AC=2OA=4,
∴BC2=AC2-AB2=36-9=27,
∴BC=.
故选:D.
【点睛】
本题考查了矩形的性质、等边三角形的判定与性质以及勾股定理;熟练掌握矩形的性质,证明三角形是等边三角形是解决问题的关键.21·cn·jy·com
3、C
【解析】
【分析】
根据正方形的性质得到AB=AD ( http: / / www.21cnjy.com ),∠BAE=∠ADF=90°,根据全等三角形的性质得到∠ABE=∠DAF,求得∠AOB=90°,根据三角形的面积公式得到OA=1,由勾股定理即可得到答案.www.21-cn-jy.com
【详解】
解:∵四边形ABCD是正方形,
∴AB=AD,∠BAE=∠ADF=90°,
在△ABE与△DAF中,
,
∴△ABE≌△DAF(SAS),
∴∠ABE=∠DAF,
∴∠ABE+∠BAO=∠DAF+∠BAO=90°,
∴∠AOB=90°,
∵△ABE≌△DAF,
∴S△ABE=S△DAF,
∴S△ABE-S△AOE=S△DAF-S△AOE,
即S△ABO=S四边形OEDF=1,
∵OA=1,
∴BO=2,
∴AB=,
故选:C.
【点睛】
本题考查了正方形的性质,全等三角形的判定和性质,勾股定理,证得△ABE≌△DAF是解题的关键.
4、C
【解析】
略
5、D
【解析】
【分析】
根据菱形的面积以及的长,求得的长,勾股定理求得边长,进而根据菱形的面积等于,即可求得答案.
【详解】
解:∵四边形是菱形
∴,
OA=4,S菱形ABCD=24,
即
中,
连接
( http: / / www.21cnjy.com / )
PE⊥AB,PF⊥AD,
S菱形ABCD=24,
故选D
【点睛】
本题考查了菱形的性质,勾股定理,掌握菱形的性质是解题的关键.
6、D
【解析】
【分析】
根据线段垂直平分线的性质得到∠BDE=∠ADE=90°,AD=BD,根据直角三角形斜边上的中线等于斜边的一半可得,CD=BD=AD=AB,由等边对等角可得∠B=∠DCE,∠A=∠ACD,设∠CDE=x,则∠B=∠DCE=2x,∠ADC=90°-x,∠A=45°+x,由直角三角形两锐角互余得45°+x+2x=90°,解得x值,即可求解.2·1·c·n·j·y
【详解】
解:由题意可知:MN为AB的垂直平分线,
∴∠BDE=∠ADE=90°,AD=BD,
∵∠ACB=90°,
∴CD=BD=AD=AB,
∴∠B=∠DCE,∠A=∠ACD,
设∠CDE=x,则∠B=∠DCE=2x,∠ADC=90°-x,
∴∠A=(180°-∠ADC)=45°+x,
∴∠A+∠B=45°+x+2x=90°,
解得:x=18°,
∴∠A=45°+x=54°,
故选:D.
【点睛】
此题考查了直角三角形斜边上的中线、线 ( http: / / www.21cnjy.com )段垂直平分线的性质、三角形外角的性质及等腰三角形的性质,注意垂直平分线上任意一点,到线段两端点的距离相等.【出处:21教育名师】
7、B
【解析】
【分析】
根据菱形的性质可证出,可将阴影部分面积转化为的面积,根据菱形的面积公式计算即可.
【详解】
解:四边形为菱形,
,,,
,
,
∴,
∴,
∴
故选:.
【点睛】
此题考查了菱形的性质,菱形的面积公式,全等三角形的判定,将阴影部分的面积转化为的面积为解题关键.
8、D
【解析】
【分析】
如图,过点作于点,连接,可说明四边形为矩形,,,是等腰直角三角形,;①中,可得为等腰直角三角形,进而求,由于四边形是平行四边形,,故可知;②,四边形为矩形,进而可求矩形的周长;③证明,由全等可知,进而可说明;④,当最小时,最小,即时,最小,计算即可;⑤在和中,勾股定理求得,将线段等量替换求解即可;⑥如图1,延长与交于点,证明,得,,,进而可说明.
【详解】
解:如图,过点作于点,连接,
( http: / / www.21cnjy.com / )
由题意知
∴四边形为平行四边形
∵
∴四边形为矩形
∴
∵
∴
∵
∴
∴是等腰直角三角形
∴
①∵,
∴为等腰直角三角形
∴
,
∴
∴四边形是平行四边形
∴
∴
故①正确;
②∵
∴四边形为矩形
∴四边形的周长
故②正确;
③四边形为矩形
∵在和中
∵
∴
∴
∴
故③正确;
④∵
当最小时,最小
∴当时,即时,的最小值等于
故④正确;
⑤在和中,,
∴
故⑤正确;
⑥如图1,延长与交于点
( http: / / www.21cnjy.com / )
∵在和中
∵
∴
∴
∵
∴
∴
故⑥正确;
综上,①②③④⑤⑥正确,
故选:.
【点睛】
本题考查了正方形,矩形的判定与性质,勾股定理,等腰直角三角形,三角形全等.解题的关键在于对知识的灵活综合运用.21*cnjy*com
9、D
【解析】
【分析】
由BE平分,得,根据正方形的性质得,,故,根据AAS得,故,设,进而可用含的式子表示出线段和的长,要求的比值即求和的比值,代入即可求解.
【详解】
∵BE平分,,
∴是等腰三角形,
∴,
四边形是正方形,
∴,,
∴,
∴,
在与中,
,
∴,
∴,
设,则,
∴,
∴,
∵,,
∴.
故选:D.
【点睛】
本题主要考查了正方形的性质,角平分线的定义以及全等三角形的判定与性质,解题的关键是将两个三角形的面积比转化成两条线段的比,综合性较强.21教育名师原创作品
10、B
【解析】
【分析】
根据两条对角线平分且相等的四边形是矩形,四条边都相等的四边形是菱形,如果对角线互相垂直平分且相等,那么这个四边形是正方形进行判断即可.
【详解】
解:①一组对边相等的四边形不一定是矩形,错误;
②两条对角线相等的平行四边形是矩形,错误;
③四条边都相等且对角线互相垂直的四边形是菱形,错误;
④四条边都相等的四边形是菱形,正确;
⑤一组邻边相等的矩形是正方形,正确.
故选:B.
【点睛】
此题考查考查平行四边形、矩形、菱形、正方形的判定方法,关键是根据矩形、正方形、菱形的判定解答.
二、填空题
1、50
【解析】
【分析】
根据直角三角形中线的性质及互为余角的性质计算.
【详解】
解:,为边上的高,
,
,是斜边上的中线,
,
,
的度数为.
故答案为:50.
【点睛】
本题主要考查了直角三角形中线的性质及互为余角的性质,解题的关键是掌握三角形中线的性质.
2、##
【解析】
【分析】
由正方形的性质得出,,,由勾股定理求出,即可得出正方形的边长与对角线长的比值.
【详解】
解:四边形是正方形,
( http: / / www.21cnjy.com / )
,,,
,
;
故答案为:.
【点睛】
本题考查了正方形的性质、勾股定理;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.
3、1.2
【解析】
【分析】
根据直角三角形斜边上的中线等于斜边的一半可得CM=AM=BM解答即可.
【详解】
解:∵M是公路AB的中点,
∴AM=BM,
∵AC⊥BC,
∴CM=AM=BM,
∵AM的长为1.2km,
∴M,C两点间的距离为1.2km.
故答案为:1.2.
【点睛】
本题考查了直角三角形斜边上的中线等于斜边的一半的性质,熟记性质是解题的关键.
4、
【解析】
【分析】
先判断出四边形ABEF是正方形,进而求出BF=2,得出BC'=,过点C'作C'H⊥BC于H,CC'与MN的交点记作点K,进而求出BH=1,再用勾股定理求出CC'=,进而得出CK=,再用勾股定理求出CN= ,最后用面积建立方程求出MN即可.21世纪教育网版权所有
【详解】
解:如图,
( http: / / www.21cnjy.com / )
∵四边形ABCD是矩形,
∴∠A=∠ABC=∠D=90°,CD=AB,BC=AD=4,
∵2AB=4,
∴AB=2,
∴CD=2,
∵将△ABF沿BF向下翻折,点A的对应点E落在线段BC上,
∴∠BEF=∠A=90°,AB=BE,
∴四边形ABEF是正方形,
∴BF是正方形ABEF的对角线,
∴∠EBF=45°,BF=AB=2,
∵C'是BF的中点,
∴BC'=BF=,
过点C'作C'H⊥BC于H,CC'与MN的交点记作点K,
在Rt△BHC'中,BH=C'H=BC'=1,
∴CH=BC﹣BH=3,
在Rt△CHC'中,CC'===,
由折叠知,CK=CC'=,
设CN=x,则HN=3﹣x,
∵将四边形CDMN沿MN向上翻折,
∴CC'⊥MN,C'N=CN=x,
在Rt△C'HN中,根据勾股定理得,C'H2+HN2=C'N2,
∴12+(3﹣x)2=x2,
∴x= ,
∴CN=,
连接CM,
∵S△CMN=CN CD=MN CK,
∴MN===,
故答案为.
【点睛】
此题主要考查了折叠的性质,矩形的性质,勾股定理和面积法解题,作出辅助线构造直角三角形求出CC'是解题的关键所在.【来源:21cnj*y.co*m】
5、6
【解析】
【分析】
由矩形的性质及直角三角形斜边上的中线的性质可求解BE=2AF=12,再利用三角形中位线定理可求解.
【详解】
解:在矩形ABCD中,∠BAD=90°,
∵F为BE的中点,AF=6,
∴BE=2AF=12.
∵G,H分别为BC,EC的中点,
∴GH=BE=6,
故答案为6.
【点睛】
根据直角三角形斜边上的中线等于斜边的一半,求解BE的长是解题的关键.再根据中位线定理求出GH.
三、解答题
1、 (1)①作图见解析;②DE=CG,证明见解析;
(2)
【解析】
【分析】
(1)①按照题意作图即可; ( http: / / www.21cnjy.com )②如图1过点D作DH⊥AC交AB于H,连接CH交DE于O,连接EH,∠A=∠B=45°,∠ADH=90°,∠A=∠DHA=45°,DA=DH= CE,四边形DHEC是平行四边形,∠DCE=90°,四边形DHEC是矩形,矩形对角线相等且互相平分可知,DE=CH,OD=OC,∠ODC=∠OCD,证明∠CDE=∠BCG=∠ACH,△ACH≌△BCG,进而可说明DE=CG.2-1-c-n-j-y
(2)如图2,由(1)可知DE=CG,CG⊥DE,S四边形CDGE DE CG CG2;可知面积最小即CG的值最短;根据垂线段最短可知,当CG⊥AB时,CG的值最短,由AG=GB,∠ACB=90°,可知CGAB=1,进而可求四边形面积的最小值.21*cnjy*com
(1)
解:①图形如图1所示.
②结论:DE=CG.
证明:如图1中,过点D作DH⊥AC交AB于H,连接CH交DE于O,连接EH.
( http: / / www.21cnjy.com / )
∵AC=BC,∠ACB=90°
∴∠A=∠B=45°
∵AD⊥DH
∴∠ADH=90°
∴∠A=∠DHA=45°
∴DA=DH
∵AD=CE
∴DH=CE
∵∠ADH=∠ACB=90°
∴DH∥BC
∴四边形DHEC是平行四边形
∵∠DCE=90°
∴四边形DHEC是矩形
∴DE=CH,OD=OC=OE=OH
∴∠ODC=∠OCD
∵CG⊥DE
∴∠CDE+∠DCG=90°,∠DCG+∠BCG=90°
∴∠CDE=∠BCG=∠ACH
在△ACH和△BCG中
∵
∴△ACH≌△BCG(ASA)
∴CH=CG
∴DE=CG.
(2)
解:如图2
( http: / / www.21cnjy.com / )
由(1)可知DE=CG,CG⊥DE
∴S四边形CDGE DE CG CG2
根据垂线段最短可知,当CG⊥AB时,CG的值最短
∵CA=CB,CG⊥AB
∴AG=GB
∴CGAB=1
∴四边形CDGE的面积的最小值为.
【点睛】
本题考查了垂线段,矩形的判定与性质,三角形全等,等腰三角形的判定与性质.解题的关键在于对知识的灵活综合运用.
2、见详解
【解析】
【分析】
先作m的垂直平分线,取m ( http: / / www.21cnjy.com )的一半为AB,然后以点A为圆心,以m长为半径画弧,交m的垂直平分线于C,连结AC,利用作一个角等于已知角,过A作BC的平行线AD,过C作AB的平行线CD,两线交于D即可.
【详解】
解:先作m的垂直平分线,取m的一半为AB,
以点A为圆心,以m长为半径画弧,交m的垂直平分线于C,连结AC,
过A作BC的平行线,与过C作AB的平行线交于D,
则四边形ABCD为所求作矩形;
( http: / / www.21cnjy.com / )
∵AD∥BC,CD∥AB,
∴四边形ABCD为平行四边形,
∵BC⊥AB,
∴∠ABC=90°,
∴四边形ABCD为矩形,
∵AB=,AC=m,
∴矩形的宽与对角线满足条件,
∴四边形ABCD为所求作矩形.
【点睛】
本题考查矩形作图,线段垂直平分线,作线段等于已知线段,平行线作法,掌握矩形作图,线段垂直平分线,作线段等于已知线段,平行线作法是解题关键.
3、 (1)①30°,②不变,30°
(2),见解析
【解析】
【分析】
(1)①先推出∠ADC=50°,在推出∠ADB=20°,从而得出结果;②同理①由AC=AD推出∠ADC=90° ,由AB=AD推出∠ADB=60° ,进而推出结果;
(2)作AF⊥CD于F,推出△ABE≌△ACF,进而得出△AEF是等边三角形,再推出△ABE是等腰直角三角形,进而得出关系.
(1)
解:①,
,
,
,
,
故答案是;
②不变,理由如下:
,
,
,
,
,
(2)
,理由如下:
如图,作于,
( http: / / www.21cnjy.com / )
,
,
,
,
,
,,,
,
,,,
即,
是等边三角形,
,
,
是等腰直角三角形,
,
是等腰直角三角形,
.
【点睛】
本题考查了旋转性质,等边三角形 ( http: / / www.21cnjy.com )性质,等腰直角三角形性质,直角三角形性质,全等三角形判定和性质等知识,解决问题的关键是找出题目中线段间的关系.
4、见解析.
【解析】
【分析】
利用正方形的性质可证明△ABE≌△ADF,可得AE=AF.
【详解】
证明:∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=90°,
∵BE=DF,
在Rt△ABE与Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(SAS),
∴AE=AF.
【点睛】
本题考查了正方形的性质,全等三角形的性质与判定,掌握正方形的性质是解题的关键.
5、 (1)证明见解析
(2)10
【解析】
【分析】
(1)利用AC平分∠BAD,AB∥CD, ( http: / / www.21cnjy.com )得到∠DAC=∠DCA,即可得到AD=DC,利用一组对边平行且相等可证明四边形ABCD是平行四边形,再结合AB=AD,即可求证结论;
(2)根据菱形的性质,得到CD=13,AO ( http: / / www.21cnjy.com )=CO=12,结合中位线性质,可得四边形BDEG是平行四边形,利用勾股定理即可得到OB、OD的长度,即可求解.
(1)
证明:∵AC平分∠BAD,AB∥CD,
∴∠DAC=∠BAC,∠DCA=∠BAC,
∴∠DAC=∠DCA,
∴AD=DC,
又∵AB∥CD,AB=AD,
∴AB∥CD且AB=CD,
∴四边形ABCD是平行四边形,
∵AB=AD,
∴四边形ABCD是菱形.
(2)
解:连接BD,交AC于点O,如图:
( http: / / www.21cnjy.com / )
∵菱形ABCD的边长为13,对角线AC=24,
∴CD=13,AO=CO=12,
∵点E、F分别是边CD、BC的中点,
∴EF∥BD(中位线),
∵AC、BD是菱形的对角线,
∴AC⊥BD,OB=OD,
又∵AB∥CD,EF∥BD,
∴DE∥BG,BD∥EG,
∵四边形BDEG是平行四边形,
∴BD=EG,
在△COD中,
∵OC⊥OD,CD=13,CO=12,
∴,
∴EG=BD=10.
【点睛】
本题考查了平行四边形性质判定方法、菱形的判 ( http: / / www.21cnjy.com )定和性质、等腰三角形性质、勾股定理等知识,关键在于熟悉四边形的判定方法和在题目中找到合适的判定条件.21教育网
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
