数学人教A版(2019)选择性必修第三册6.3.1二项式定理(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册6.3.1二项式定理(共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 188.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-12 16:53:36 | ||
图片预览




文档简介
(共15张PPT)
6.3.1二项式定理
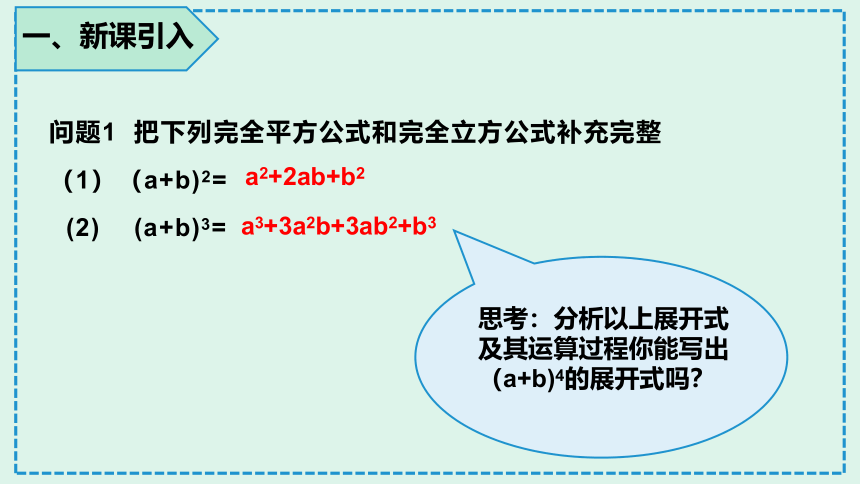
问题1 把下列完全平方公式和完全立方公式补充完整
(1)(a+b)2=
(2) (a+b)3=
一、新课引入
a2+2ab+b2
a3+3a2b+3ab2+b3
思考:分析以上展开式及其运算过程你能写出(a+b)4的展开式吗?
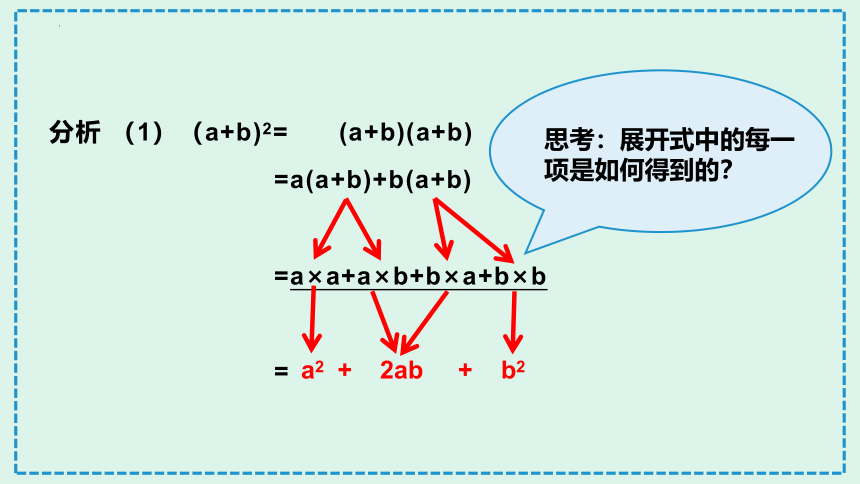
分析 (1)(a+b)2= (a+b)(a+b)
=a(a+b)+b(a+b)
=a×a+a×b+b×a+b×b
=
a2 + 2ab + b2
思考:展开式中的每一项是如何得到的?
分析(2) (a+b)3=(a+b)(a+b)(a+b)
=a×a×a+a×a×b+a×b×a+b×a×a
+a×b×b+b×a×b+b×b×a+b×b×b
=
a3+3a2b+3ab2+b3
思考:分析以上展开式及其运算过程你能写出(a+b)4的展开式吗?
(从3个括号中选一个括号出1个b,有 种选法)
(从3个括号中选2个括号各出1个b,有 种选法)
(a+b)4=(a+b)(a+b)(a+b)(a+b) =a×a×a×a
+a×a×a×b+a×a×b×a+a×b×a×a+b×a×a×a
+a×a×b×b+ +b×b×a×a
+a×b×b×b+ +b×b×b×a+b×b×b×b
(从4个括号选1个括号出1个b,有 种选法)
(从4个括号选2个括号各出1个b,有 种选法)
(从4个括号选3个括号分别各出1个b,有 种选法)
(a+b)4=(a+b)(a+b)(a+b)(a+b)
所以,= a4 + a3b+ a2b2+ ab3+ b4
思考:仿照上述过程,根据(a+b)2, (a+b)3,
(a+b)4的展开式,能否猜想出(a+b)n的展开式?
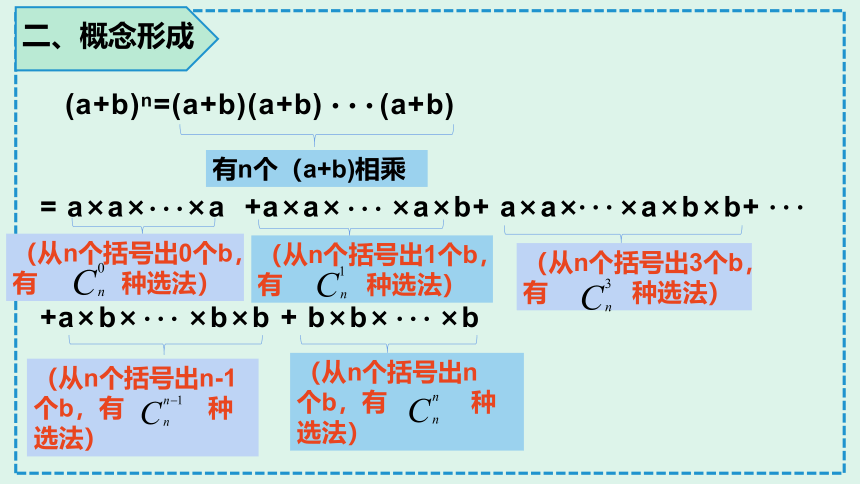
(a+b)n=(a+b)(a+b) (a+b)
= a×a× ×a +a×a× ×a×b+ a×a× ×a×b×b+
+a×b× ×b×b + b×b× ×b
二、概念形成
有n个(a+b)相乘
(从n个括号出0个b,
有 种选法)
(从n个括号出1个b,
有 种选法)
(从n个括号出3个b,
有 种选法)
(从n个括号出n-1
个b,有 种选法)
(从n个括号出n
个b,有 种选法)
因此,(a+b)n的展开式如下:
(a+b)n=(a+b)(a+b) (a+b)
= an+ an-1b1+ an-2b2+ + an-kbk+ +
a1bn-1+ bn ,(n∈N*)
1)该公式叫做二项式定理,右边的多项式叫做(a+b)n的二项展开式;
2)各项的系数 (k=0,1,2, ,n)叫做二项式系数;
3)其中 an-kbk叫做二项展开式的通项,用Tk+1表示,即通项为展开式的第k+1项,且Tk+1= an-kbk
思考1:各项的次数有什么规律?
思考2:若令a=1,b=x,你能写出二项式的展开式吗?
解:各项的次数都等于(a+b)n的次数
解:(1+x)n= + x1+ x2+ + xk+
+ xn
三、例题讲解
例1 求 的展开式
解:根据二项式定理,
例2 (1)求(1+2x)7的展开式的第4项的系数;
(2)求 的展开式中x2的系数。
解:(1) (1+2x)7的展开式的第4项是
T3+1
因此,展开式第4项的系数是280
解:(2) 的展开式的通项是
四、随堂小练
1、写出(p+q)5的展开式。
2、求(2a+3b)6的展开式的第3项。
3、(x-1)10的展开式的第6项的系数是( )
A. B. C. D.
D
五、总结归纳
1、二项式定理的内容是什么?
(a+b)n=
= an+ an-1b1+ an-2b2+ + an-kbk+
+ a1bn-1+ bn ,(n∈N*)
2、二项式展开式的通项如何表示?
通项为Tk+1= an-kbk
谢谢观看
THANKS!
6.3.1二项式定理
问题1 把下列完全平方公式和完全立方公式补充完整
(1)(a+b)2=
(2) (a+b)3=
一、新课引入
a2+2ab+b2
a3+3a2b+3ab2+b3
思考:分析以上展开式及其运算过程你能写出(a+b)4的展开式吗?
分析 (1)(a+b)2= (a+b)(a+b)
=a(a+b)+b(a+b)
=a×a+a×b+b×a+b×b
=
a2 + 2ab + b2
思考:展开式中的每一项是如何得到的?
分析(2) (a+b)3=(a+b)(a+b)(a+b)
=a×a×a+a×a×b+a×b×a+b×a×a
+a×b×b+b×a×b+b×b×a+b×b×b
=
a3+3a2b+3ab2+b3
思考:分析以上展开式及其运算过程你能写出(a+b)4的展开式吗?
(从3个括号中选一个括号出1个b,有 种选法)
(从3个括号中选2个括号各出1个b,有 种选法)
(a+b)4=(a+b)(a+b)(a+b)(a+b) =a×a×a×a
+a×a×a×b+a×a×b×a+a×b×a×a+b×a×a×a
+a×a×b×b+ +b×b×a×a
+a×b×b×b+ +b×b×b×a+b×b×b×b
(从4个括号选1个括号出1个b,有 种选法)
(从4个括号选2个括号各出1个b,有 种选法)
(从4个括号选3个括号分别各出1个b,有 种选法)
(a+b)4=(a+b)(a+b)(a+b)(a+b)
所以,= a4 + a3b+ a2b2+ ab3+ b4
思考:仿照上述过程,根据(a+b)2, (a+b)3,
(a+b)4的展开式,能否猜想出(a+b)n的展开式?
(a+b)n=(a+b)(a+b) (a+b)
= a×a× ×a +a×a× ×a×b+ a×a× ×a×b×b+
+a×b× ×b×b + b×b× ×b
二、概念形成
有n个(a+b)相乘
(从n个括号出0个b,
有 种选法)
(从n个括号出1个b,
有 种选法)
(从n个括号出3个b,
有 种选法)
(从n个括号出n-1
个b,有 种选法)
(从n个括号出n
个b,有 种选法)
因此,(a+b)n的展开式如下:
(a+b)n=(a+b)(a+b) (a+b)
= an+ an-1b1+ an-2b2+ + an-kbk+ +
a1bn-1+ bn ,(n∈N*)
1)该公式叫做二项式定理,右边的多项式叫做(a+b)n的二项展开式;
2)各项的系数 (k=0,1,2, ,n)叫做二项式系数;
3)其中 an-kbk叫做二项展开式的通项,用Tk+1表示,即通项为展开式的第k+1项,且Tk+1= an-kbk
思考1:各项的次数有什么规律?
思考2:若令a=1,b=x,你能写出二项式的展开式吗?
解:各项的次数都等于(a+b)n的次数
解:(1+x)n= + x1+ x2+ + xk+
+ xn
三、例题讲解
例1 求 的展开式
解:根据二项式定理,
例2 (1)求(1+2x)7的展开式的第4项的系数;
(2)求 的展开式中x2的系数。
解:(1) (1+2x)7的展开式的第4项是
T3+1
因此,展开式第4项的系数是280
解:(2) 的展开式的通项是
四、随堂小练
1、写出(p+q)5的展开式。
2、求(2a+3b)6的展开式的第3项。
3、(x-1)10的展开式的第6项的系数是( )
A. B. C. D.
D
五、总结归纳
1、二项式定理的内容是什么?
(a+b)n=
= an+ an-1b1+ an-2b2+ + an-kbk+
+ a1bn-1+ bn ,(n∈N*)
2、二项式展开式的通项如何表示?
通项为Tk+1= an-kbk
谢谢观看
THANKS!
