新课标苏教版六上3.8《按比分配的实际问题》课件(30张PPT)
文档属性
| 名称 | 新课标苏教版六上3.8《按比分配的实际问题》课件(30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 09:10:48 | ||
图片预览








文档简介
(共30张PPT)
按比分配的实际问题
苏教版六年级上册
教学目标
1.学习目标描述:在自主探索学习中理解按比分配的意义,掌握按比分配应用题的结构特点以及解题方法,能准确解答按比分配应用题。
2.学习内容分析:按比分配是把比的知识应用于解决相关的实际问题的一个课例。即把一个数量按照一定的比进行分配。它是在学生学习了比与分数的联系,已掌握“平均分”和“分数应用题”的基础上进行教学的延伸。教材提供了两种解法, 一是转化为归一应用题,使用归
教学目标
一应用题的解题方法解答。二是把比转化成份数,注意联系生活工作实际导入例题,使学生从再转化成分数,使题目成为分数乘法应用题,然后按求一个数的几分之几是多少的方法来解答。
3.学科核心素养分析:在经历用比描述生活现象、解决简单实际问题的过程中,进一步体会比的意义,感受比在生活中的广泛应用,提高解决问题的能力,激发学生学习数学的兴趣,感受学习数学的价值,增强学生的应用意识。
新知导入
1.填一填。
红绸花与黄绸花的数量比是3:4。
红绸花占( )份,黄绸花占( )份,两种绸花的总数就有这样的( )份。
红绸花的数量是两种绸花总数的( );黄绸花的数量是两种绸花总数的( )。
3
4
7
3
7
4
7
新知导入
2.明明做了35朵红绸花与黄绸花,其中红绸花占总数的 ,那么红绸花有多少朵?
3
7
求一个数的几分之几是多少,用乘法计算。
35× =15(朵)
3
7
答:红绸花有15朵。
新知导入
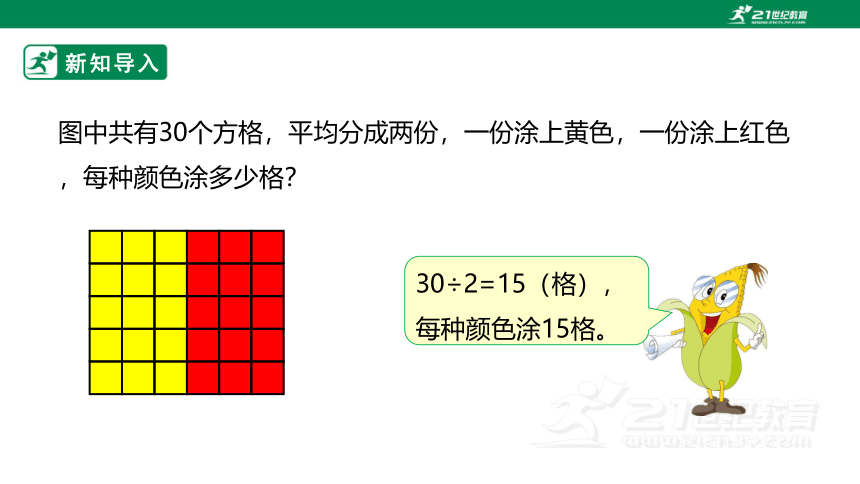
图中共有30个方格,平均分成两份,一份涂上黄色,一份涂上红色,每种颜色涂多少格?
30÷2=15(格),每种颜色涂15格。
新知导入
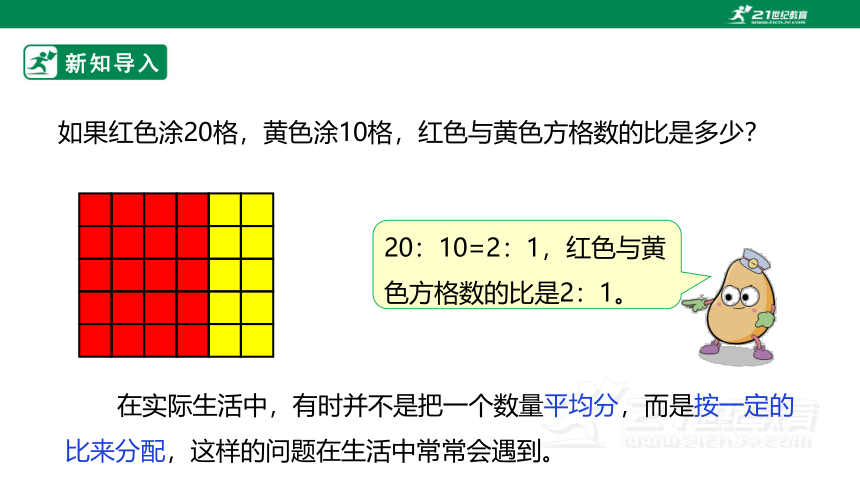
如果红色涂20格,黄色涂10格,红色与黄色方格数的比是多少?
20:10=2:1,红色与黄色方格数的比是2:1。
在实际生活中,有时并不是把一个数量平均分,而是按一定的比来分配,这样的问题在生活中常常会遇到。
新知讲解
把30个方格涂上红色和黄色,使红色与黄色方格数的比是3:2。两种颜色各应涂多少格?先算一算,再涂一涂。
怎样理解“红色与黄色方格数的比是3:2”?分组交流。
就是把30个方格平均分成5份,其中3份涂红色,2份涂黄色。
新知讲解
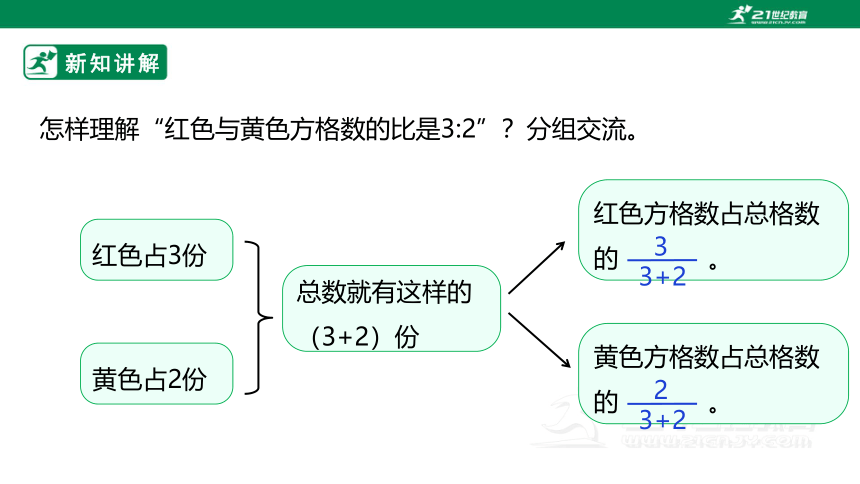
怎样理解“红色与黄色方格数的比是3:2”?分组交流。
红色占3份
黄色占2份
总数就有这样的(3+2)份
红色方格数占总格数的 。
3
3+2
黄色方格数占总格数的 。
2
3+2
新知讲解
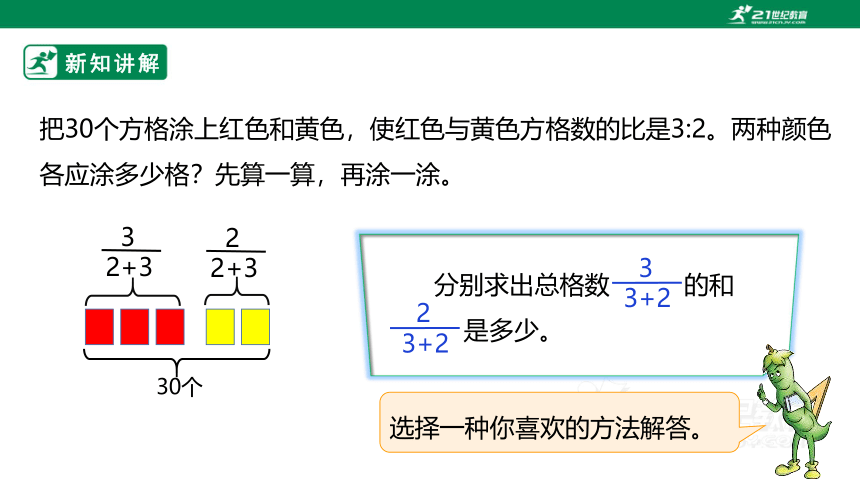
把30个方格涂上红色和黄色,使红色与黄色方格数的比是3:2。两种颜色各应涂多少格?先算一算,再涂一涂。
思考:
两种方格数各有多少格呢?你准备怎样解决这个问题,用你学过的知识来试试。
新知讲解
把30个方格涂上红色和黄色,使红色与黄色方格数的比是3:2。两种颜色各应涂多少格?先算一算,再涂一涂。
30个
先算每份有多少格,再分别算出红色和黄色方格各有多少格。
新知讲解
把30个方格涂上红色和黄色,使红色与黄色方格数的比是3:2。两种颜色各应涂多少格?先算一算,再涂一涂。
30个
3
2+3
2
2+3
分别求出总格数 的和
是多少。
3
3+2
2
3+2
选择一种你喜欢的方法解答。
新知讲解
把30个方格涂上红色和黄色,使红色与黄色方格数的比是3:2。两种颜色各应涂多少格?先算一算,再涂一涂。
30÷(3+2)=6(格)
6×3=18(格)
6×2=12(格)
30× =18(格)
3
3+2
30× =12(格)
2
3+2
新知讲解
这样解答正确吗?如何进行检验?与同伴交流自己的想法。
可以把求得的红色和黄色方格数相加,看是不是等于总方格数。
可以涂一涂,看看是不是正好涂满。
还可以把求得的红色和黄色方格数写成比的形式,看化简后是不是等于3∶2。
新知讲解
选择自己喜欢的方法检验一下自己的结果,并写出答语。
30× =18(格)
3
3+2
30× =12(格)
2
3+2
18+12=30(格),等于总方格数。
正好涂满
18:12=3:2,是等于3∶2。
答:红色应涂18格,黄色应涂12格。
新知讲解
想一想:如果把上图的30个方格按1:2:3涂成红、黄、绿三种颜色,求三种颜色各应涂多少格,又该怎样解答?
怎么理解的?
红色占1份,黄色占2份,绿色占3份,一共有1+2+3=6份。
红色方格数各占方格总数的 ,
黄色方格数各占方格总数的 ,绿色方格数各占方格总数的 。
1
6
2
6
3
6
新知讲解
想一想:如果把上图的30个方格按1:2:3涂成红、黄、绿三种颜色,求三种颜色各应涂多少格。用你喜欢的方法算算,并进行检验。
30÷(1+2+3)=5(格)
5×1=5(格)
5×2=10(格)
5×3=15(格)
答:红色应涂5格,黄色应涂10格,绿色应涂15格。
30× =5(格)
1
1+2+3
30× =10(格)
2
1+2+3
30× =15(格)
3
1+2+3
新知讲解
今天我们学习的两道道题目有什么共同特点?是怎么解答的?
特点:已知总数量和各部分量的比,求各部分量。
求总份数,再求出每份的具体数量,最后求出各部分量。
求总份数,得出各部分量占总数量的几分之几,最后求各部分量。
新知讲解
像这样把一个数量按照一定的比来进行分配,这种分配方法通常叫作按比分配。 按比分配问题要巧妙利用题目中的比,把它转化成求总量的几分之几是多少的问题来解。
新知讲解
试一试
三个小组去植树,植树棵树按各小组人数的比分配。每个小组各应植树多少棵?
怎样理解“植树棵树按各小组人数的比分配”?
三个组人数的比是8:7:9,就是按8:7:9分配。
新知讲解
三个小组去植树,植树棵树按各小组人数的比分配。每个小组各应植树多少棵?
72÷(8+7+9)=3(棵)
3×8=24(棵)
3×7=21(棵)
3×9=27(棵)
答:一组植树24棵,二组植树21棵,三组植树27棵。
30× =24(棵)
8
8+7+9
30× =21(棵)
7
8+7+9
30× =27(棵)
9
8+7+9
课堂练习
1.果园里梨树与桃树的棵数比为2:3,已知梨树和桃树共100棵,梨树与桃树各有多少棵?
2+3=5
100× =
2
5
40(棵)
100× =
3
5
60(棵)
答:梨树有40棵,桃树有60棵。
课堂练习
2.
果园里梨树与桃树的棵数比为2:3,已知桃树比梨树少100棵,梨树与桃树各有多少棵?
桃树比梨树少(3-2)份,先求出一份的量。
100÷(3-2)=100(棵)
100×2=200(棵)
100×3=300(棵)
答:梨树有200棵,桃树有300棵。
课堂练习
3.果园里梨树与桃树的棵数比为2:3,已知梨树有100棵,桃树有多少棵?
梨树占2份,正好是100棵,先求出一份的量。
100÷2=50(棵)
50×3=150(棵)
答:桃树有150棵。
课堂练习
4.拓展应用:把下面的三角形分成两部分,使这两部分的面积比是1:3,你能分一分吗?
实际上,任意三角形把底平均分成四份,把顶点与一份处连接,分成两个三角形,它们等高,底是1:3,面积就是1:3。
课堂总结
通过今天的学习,你有哪些收获?
我知道按比分配问题的特点了。
我学会解决按比分配的问题了。
板书设计
按比分配的实际问题
特点:已知总数量和各部分量的比,求各部分量。
解答方法:
(1)总份数 → 每份的具体数量 → 各部分量
(2)总份数 → 各部分量占总数量的几分之几 → 各部分量
作业布置
完成课本第60页“练一练”习题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
按比分配的实际问题
苏教版六年级上册
教学目标
1.学习目标描述:在自主探索学习中理解按比分配的意义,掌握按比分配应用题的结构特点以及解题方法,能准确解答按比分配应用题。
2.学习内容分析:按比分配是把比的知识应用于解决相关的实际问题的一个课例。即把一个数量按照一定的比进行分配。它是在学生学习了比与分数的联系,已掌握“平均分”和“分数应用题”的基础上进行教学的延伸。教材提供了两种解法, 一是转化为归一应用题,使用归
教学目标
一应用题的解题方法解答。二是把比转化成份数,注意联系生活工作实际导入例题,使学生从再转化成分数,使题目成为分数乘法应用题,然后按求一个数的几分之几是多少的方法来解答。
3.学科核心素养分析:在经历用比描述生活现象、解决简单实际问题的过程中,进一步体会比的意义,感受比在生活中的广泛应用,提高解决问题的能力,激发学生学习数学的兴趣,感受学习数学的价值,增强学生的应用意识。
新知导入
1.填一填。
红绸花与黄绸花的数量比是3:4。
红绸花占( )份,黄绸花占( )份,两种绸花的总数就有这样的( )份。
红绸花的数量是两种绸花总数的( );黄绸花的数量是两种绸花总数的( )。
3
4
7
3
7
4
7
新知导入
2.明明做了35朵红绸花与黄绸花,其中红绸花占总数的 ,那么红绸花有多少朵?
3
7
求一个数的几分之几是多少,用乘法计算。
35× =15(朵)
3
7
答:红绸花有15朵。
新知导入
图中共有30个方格,平均分成两份,一份涂上黄色,一份涂上红色,每种颜色涂多少格?
30÷2=15(格),每种颜色涂15格。
新知导入
如果红色涂20格,黄色涂10格,红色与黄色方格数的比是多少?
20:10=2:1,红色与黄色方格数的比是2:1。
在实际生活中,有时并不是把一个数量平均分,而是按一定的比来分配,这样的问题在生活中常常会遇到。
新知讲解
把30个方格涂上红色和黄色,使红色与黄色方格数的比是3:2。两种颜色各应涂多少格?先算一算,再涂一涂。
怎样理解“红色与黄色方格数的比是3:2”?分组交流。
就是把30个方格平均分成5份,其中3份涂红色,2份涂黄色。
新知讲解
怎样理解“红色与黄色方格数的比是3:2”?分组交流。
红色占3份
黄色占2份
总数就有这样的(3+2)份
红色方格数占总格数的 。
3
3+2
黄色方格数占总格数的 。
2
3+2
新知讲解
把30个方格涂上红色和黄色,使红色与黄色方格数的比是3:2。两种颜色各应涂多少格?先算一算,再涂一涂。
思考:
两种方格数各有多少格呢?你准备怎样解决这个问题,用你学过的知识来试试。
新知讲解
把30个方格涂上红色和黄色,使红色与黄色方格数的比是3:2。两种颜色各应涂多少格?先算一算,再涂一涂。
30个
先算每份有多少格,再分别算出红色和黄色方格各有多少格。
新知讲解
把30个方格涂上红色和黄色,使红色与黄色方格数的比是3:2。两种颜色各应涂多少格?先算一算,再涂一涂。
30个
3
2+3
2
2+3
分别求出总格数 的和
是多少。
3
3+2
2
3+2
选择一种你喜欢的方法解答。
新知讲解
把30个方格涂上红色和黄色,使红色与黄色方格数的比是3:2。两种颜色各应涂多少格?先算一算,再涂一涂。
30÷(3+2)=6(格)
6×3=18(格)
6×2=12(格)
30× =18(格)
3
3+2
30× =12(格)
2
3+2
新知讲解
这样解答正确吗?如何进行检验?与同伴交流自己的想法。
可以把求得的红色和黄色方格数相加,看是不是等于总方格数。
可以涂一涂,看看是不是正好涂满。
还可以把求得的红色和黄色方格数写成比的形式,看化简后是不是等于3∶2。
新知讲解
选择自己喜欢的方法检验一下自己的结果,并写出答语。
30× =18(格)
3
3+2
30× =12(格)
2
3+2
18+12=30(格),等于总方格数。
正好涂满
18:12=3:2,是等于3∶2。
答:红色应涂18格,黄色应涂12格。
新知讲解
想一想:如果把上图的30个方格按1:2:3涂成红、黄、绿三种颜色,求三种颜色各应涂多少格,又该怎样解答?
怎么理解的?
红色占1份,黄色占2份,绿色占3份,一共有1+2+3=6份。
红色方格数各占方格总数的 ,
黄色方格数各占方格总数的 ,绿色方格数各占方格总数的 。
1
6
2
6
3
6
新知讲解
想一想:如果把上图的30个方格按1:2:3涂成红、黄、绿三种颜色,求三种颜色各应涂多少格。用你喜欢的方法算算,并进行检验。
30÷(1+2+3)=5(格)
5×1=5(格)
5×2=10(格)
5×3=15(格)
答:红色应涂5格,黄色应涂10格,绿色应涂15格。
30× =5(格)
1
1+2+3
30× =10(格)
2
1+2+3
30× =15(格)
3
1+2+3
新知讲解
今天我们学习的两道道题目有什么共同特点?是怎么解答的?
特点:已知总数量和各部分量的比,求各部分量。
求总份数,再求出每份的具体数量,最后求出各部分量。
求总份数,得出各部分量占总数量的几分之几,最后求各部分量。
新知讲解
像这样把一个数量按照一定的比来进行分配,这种分配方法通常叫作按比分配。 按比分配问题要巧妙利用题目中的比,把它转化成求总量的几分之几是多少的问题来解。
新知讲解
试一试
三个小组去植树,植树棵树按各小组人数的比分配。每个小组各应植树多少棵?
怎样理解“植树棵树按各小组人数的比分配”?
三个组人数的比是8:7:9,就是按8:7:9分配。
新知讲解
三个小组去植树,植树棵树按各小组人数的比分配。每个小组各应植树多少棵?
72÷(8+7+9)=3(棵)
3×8=24(棵)
3×7=21(棵)
3×9=27(棵)
答:一组植树24棵,二组植树21棵,三组植树27棵。
30× =24(棵)
8
8+7+9
30× =21(棵)
7
8+7+9
30× =27(棵)
9
8+7+9
课堂练习
1.果园里梨树与桃树的棵数比为2:3,已知梨树和桃树共100棵,梨树与桃树各有多少棵?
2+3=5
100× =
2
5
40(棵)
100× =
3
5
60(棵)
答:梨树有40棵,桃树有60棵。
课堂练习
2.
果园里梨树与桃树的棵数比为2:3,已知桃树比梨树少100棵,梨树与桃树各有多少棵?
桃树比梨树少(3-2)份,先求出一份的量。
100÷(3-2)=100(棵)
100×2=200(棵)
100×3=300(棵)
答:梨树有200棵,桃树有300棵。
课堂练习
3.果园里梨树与桃树的棵数比为2:3,已知梨树有100棵,桃树有多少棵?
梨树占2份,正好是100棵,先求出一份的量。
100÷2=50(棵)
50×3=150(棵)
答:桃树有150棵。
课堂练习
4.拓展应用:把下面的三角形分成两部分,使这两部分的面积比是1:3,你能分一分吗?
实际上,任意三角形把底平均分成四份,把顶点与一份处连接,分成两个三角形,它们等高,底是1:3,面积就是1:3。
课堂总结
通过今天的学习,你有哪些收获?
我知道按比分配问题的特点了。
我学会解决按比分配的问题了。
板书设计
按比分配的实际问题
特点:已知总数量和各部分量的比,求各部分量。
解答方法:
(1)总份数 → 每份的具体数量 → 各部分量
(2)总份数 → 各部分量占总数量的几分之几 → 各部分量
作业布置
完成课本第60页“练一练”习题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
