五年级上册数学课件梯形的面积沪教版(共14张PPT)
文档属性
| 名称 | 五年级上册数学课件梯形的面积沪教版(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 508.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-12 00:00:00 | ||
图片预览


文档简介
(共14张PPT)
沪教版五年级数学上册
本节课我们来继续学习梯形的面积,在掌握用拼、割两种方法推导梯形的面积公式的基础上我们来探究梯形的中位线和梯形的面积的关系,同学们要理解并掌握用梯形的中位线表示梯形面积的方法,并能解决实际的问题。
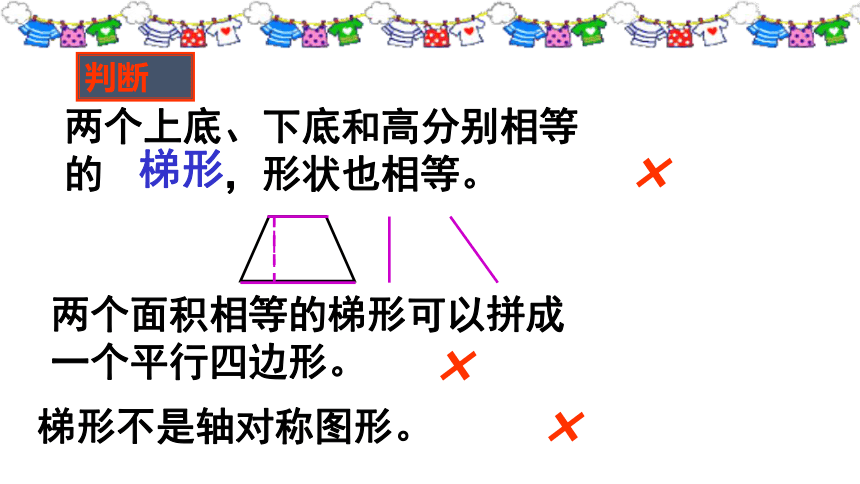
梯形
两个上底、下底和高分别相等
的 ,形状也相等。
判断
×
两个面积相等的梯形可以拼成
一个平行四边形。
×
梯形不是轴对称图形。
×
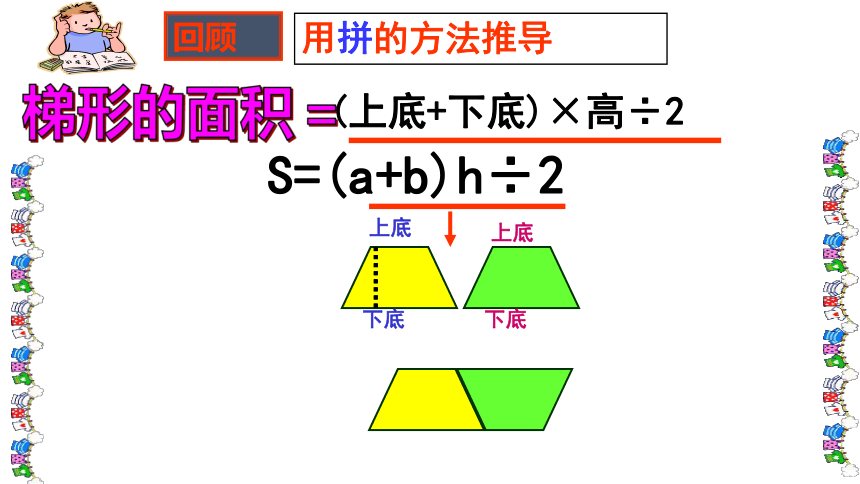
回顾
(上底+下底)×高÷2
S=(a+b)h÷2
上底
下底
上底
下底
用拼的方法推导
+
上底
下底
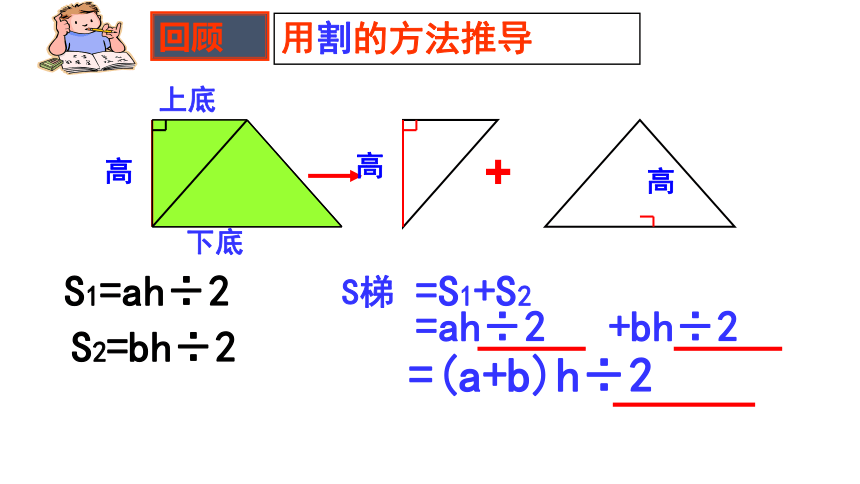
高
高
高
S1=ah÷2
S2=bh÷2
S梯
=S1+S2
=ah÷2
+bh÷2
=(a+b)h÷2
用割的方法推导
回顾
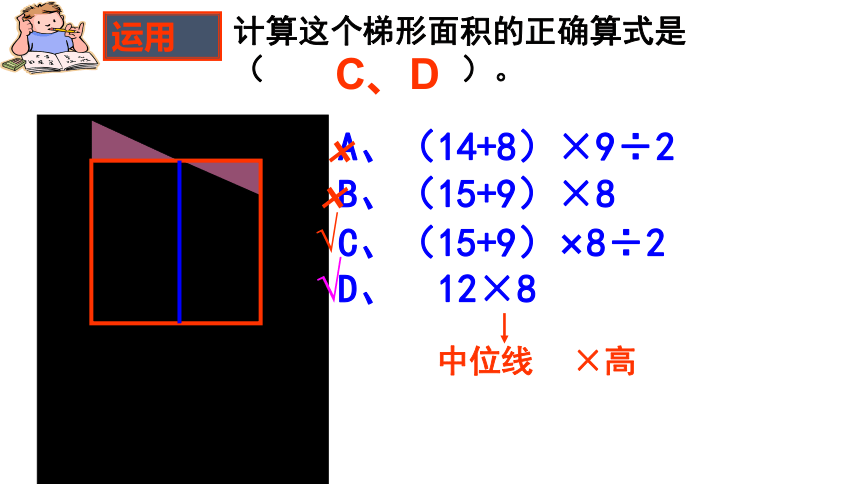
运用
8
15
9
14
12
(单位:㎝)
计算这个梯形面积的正确算式是
( )。
A、(14+8)×9÷2
B、(15+9)×8
C、(15+9)×8÷2
D、 12×8
×
×
√
√
中位线
×高
C、D
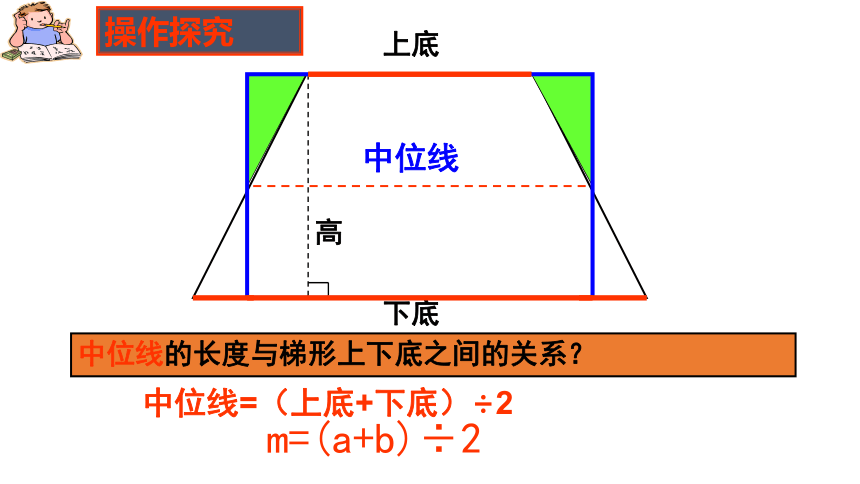
操作探究
上底
下底
高
中位线
中位线的长度与梯形上下底之间的关系?
中位线=(上底+下底)÷2
m=(a+b)÷2
中位线
25㎝
中位线=(上底+下底)÷2
28㎝
25×2-28
用割补的方法推导
上底
下底
高
中位线
S=mh
梯形面积=中位线×高
归纳
梯形的面积=(上底+下底)×高÷2
S=(a+b)h÷2
S=(a+b)÷2×h
中位线
×高
梯形的面积=
S=mh
7
3
6
5.5
运用(求梯形的中位线)单位:厘米
解:m=(a+b)÷2
=(3+7)÷2
=5(㎝)
18
10
22
20
解:m=(a+b)÷2
=(18+10)÷2
=14(㎝)
运用(求梯形的中位线)单位:厘米
填表(单位:cm)
图形
梯形
梯形
底
高
中位线
面积
a 14
b 6
a 8
b
10
75
梯形
7.5
5
30
6
4
a 10
b 2
48
8
6
?
本节课我们主要学习了用梯形的中位线来求梯形的面积,你学习的怎么样?和同桌说一说这一节课你都掌握了哪些内容?
沪教版五年级数学上册
本节课我们来继续学习梯形的面积,在掌握用拼、割两种方法推导梯形的面积公式的基础上我们来探究梯形的中位线和梯形的面积的关系,同学们要理解并掌握用梯形的中位线表示梯形面积的方法,并能解决实际的问题。
梯形
两个上底、下底和高分别相等
的 ,形状也相等。
判断
×
两个面积相等的梯形可以拼成
一个平行四边形。
×
梯形不是轴对称图形。
×
回顾
(上底+下底)×高÷2
S=(a+b)h÷2
上底
下底
上底
下底
用拼的方法推导
+
上底
下底
高
高
高
S1=ah÷2
S2=bh÷2
S梯
=S1+S2
=ah÷2
+bh÷2
=(a+b)h÷2
用割的方法推导
回顾
运用
8
15
9
14
12
(单位:㎝)
计算这个梯形面积的正确算式是
( )。
A、(14+8)×9÷2
B、(15+9)×8
C、(15+9)×8÷2
D、 12×8
×
×
√
√
中位线
×高
C、D
操作探究
上底
下底
高
中位线
中位线的长度与梯形上下底之间的关系?
中位线=(上底+下底)÷2
m=(a+b)÷2
中位线
25㎝
中位线=(上底+下底)÷2
28㎝
25×2-28
用割补的方法推导
上底
下底
高
中位线
S=mh
梯形面积=中位线×高
归纳
梯形的面积=(上底+下底)×高÷2
S=(a+b)h÷2
S=(a+b)÷2×h
中位线
×高
梯形的面积=
S=mh
7
3
6
5.5
运用(求梯形的中位线)单位:厘米
解:m=(a+b)÷2
=(3+7)÷2
=5(㎝)
18
10
22
20
解:m=(a+b)÷2
=(18+10)÷2
=14(㎝)
运用(求梯形的中位线)单位:厘米
填表(单位:cm)
图形
梯形
梯形
底
高
中位线
面积
a 14
b 6
a 8
b
10
75
梯形
7.5
5
30
6
4
a 10
b 2
48
8
6
?
本节课我们主要学习了用梯形的中位线来求梯形的面积,你学习的怎么样?和同桌说一说这一节课你都掌握了哪些内容?
同课章节目录
