第一单元极速提分法第2招 长方体、正方体体积的解题技巧(共17张PPT)
文档属性
| 名称 | 第一单元极速提分法第2招 长方体、正方体体积的解题技巧(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-12 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第2招 长方体、正方体体积的解题技巧
学习第1单元后使用
SJ 六年级上册
计算长方体、正方体的体积可以运用公式V=abh,V=a3,V=Sh直接计算,还可以运用等积变形法、排水法、表面积的变化等方法进行计算。
把两个完全一样的小长方体拼成一个大长方体(如图),这个大长方体的表面积比原来两个小长方体的表面积之和减少了50 cm2,如果拼成的大长方体的长是
20 cm,那么一个小长方体的体积是
多少立方厘米?
经典例题
由图可知减少了两个侧面面积,
表面积之和减少了50 cm2,那么可求一个侧面面积,大长方体的长是20 cm,那么可求小长方体的长
侧面面积×长就是一个小长方体的体积。
规范解答:
50÷2×(20÷2)=250(cm3)
答:一个小长方体的体积是250 cm3。
1
3
5
提示:点击 进入题组训练
用“等积变形法”解决问题
用“排水法”解决问题
用“公式法”求体积
2
4
6
用“操作法”求容积
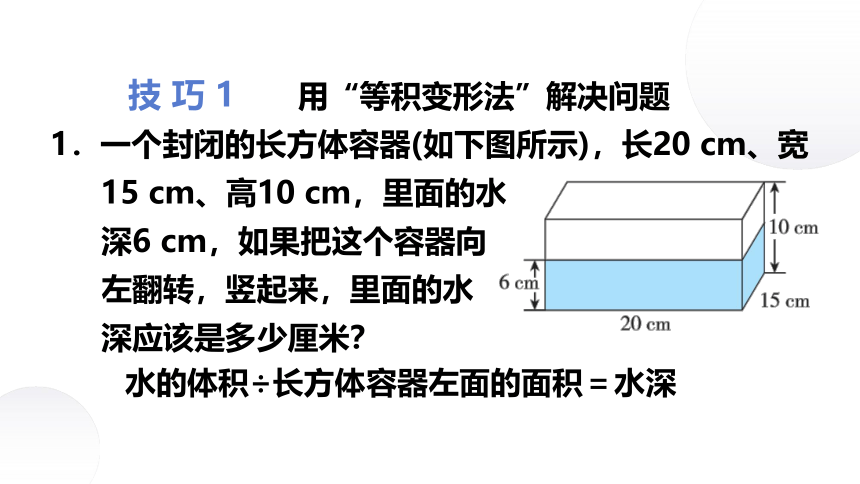
1.一个封闭的长方体容器(如下图所示),长20 cm、宽15 cm、高10 cm,里面的水
深6 cm,如果把这个容器向
左翻转,竖起来,里面的水
深应该是多少厘米?
用“等积变形法”解决问题
技 巧 1
水的体积÷长方体容器左面的面积=水深
20×15×6÷(15×10)=12(cm)
答:里面的水深是12 cm。
2. 如图,有一块长方形地,A处比B处高5 m,现在要使A,B两处高度相同,要从A处取多少米厚的土填在B处?
(10-6)×6×5÷(10×6)=2(m)
5-2=3(m)
答:要从A处取3 m厚的土填在B处。
体积=底面积×高
3.有一个长方体容器长90 cm,宽45 cm,高40 cm,水深25 cm,现在在里面沉入一个棱长为18 cm的正方体铁块,这时水深多少厘米?
用“排水法”解决问题
技 巧 2
25+18×18×18÷(90×45)=26.44(cm)
答:这时水深26.44 cm。
水位上涨部分的体积=正方体的体积
4.有一个长方体水箱,从里面量长40 cm,宽30 cm,深35 cm,箱中水面高10 cm。放入一个棱长为
20 cm的正方体铁块后,铁块顶部仍高于水面。这时水面上升了多少厘米?
铁块放入后,该长方体水箱可以看成一个环形水箱,根据此时水箱底面积可求水面高度
40×30×10÷(40×30-20×20)-10=5(cm)
答:这时水面上升了5 cm。
用“公式法”求体积
技 巧 3
5.一个长方体的表面积是67.92 dm2,底面积是19 dm2,底面周长是17.6 dm,这个长方体的体积是多少立方分米?
表面积-底面积×2=侧面积,
侧面积÷底面周长=高,
底面积×高=体积。
67.92-19×2=29.92(dm2)
29.92÷17.6=1.7(dm)
19×1.7=32.3(dm3)
答:这个长方体的体积是32.3 dm3。
用“操作法”求容积
技 巧 4
6.用一张长40 cm、宽20 cm的铁皮做一个深5 cm的无盖铁皮盒子,怎样做能使铁皮盒子的容积最大?并求出最大容积。(请画图表示制作方法)
(40-5×4)×20×5=2000(cm3)
答:最大容积是2000 cm3。
Thank you!
第2招 长方体、正方体体积的解题技巧
学习第1单元后使用
SJ 六年级上册
计算长方体、正方体的体积可以运用公式V=abh,V=a3,V=Sh直接计算,还可以运用等积变形法、排水法、表面积的变化等方法进行计算。
把两个完全一样的小长方体拼成一个大长方体(如图),这个大长方体的表面积比原来两个小长方体的表面积之和减少了50 cm2,如果拼成的大长方体的长是
20 cm,那么一个小长方体的体积是
多少立方厘米?
经典例题
由图可知减少了两个侧面面积,
表面积之和减少了50 cm2,那么可求一个侧面面积,大长方体的长是20 cm,那么可求小长方体的长
侧面面积×长就是一个小长方体的体积。
规范解答:
50÷2×(20÷2)=250(cm3)
答:一个小长方体的体积是250 cm3。
1
3
5
提示:点击 进入题组训练
用“等积变形法”解决问题
用“排水法”解决问题
用“公式法”求体积
2
4
6
用“操作法”求容积
1.一个封闭的长方体容器(如下图所示),长20 cm、宽15 cm、高10 cm,里面的水
深6 cm,如果把这个容器向
左翻转,竖起来,里面的水
深应该是多少厘米?
用“等积变形法”解决问题
技 巧 1
水的体积÷长方体容器左面的面积=水深
20×15×6÷(15×10)=12(cm)
答:里面的水深是12 cm。
2. 如图,有一块长方形地,A处比B处高5 m,现在要使A,B两处高度相同,要从A处取多少米厚的土填在B处?
(10-6)×6×5÷(10×6)=2(m)
5-2=3(m)
答:要从A处取3 m厚的土填在B处。
体积=底面积×高
3.有一个长方体容器长90 cm,宽45 cm,高40 cm,水深25 cm,现在在里面沉入一个棱长为18 cm的正方体铁块,这时水深多少厘米?
用“排水法”解决问题
技 巧 2
25+18×18×18÷(90×45)=26.44(cm)
答:这时水深26.44 cm。
水位上涨部分的体积=正方体的体积
4.有一个长方体水箱,从里面量长40 cm,宽30 cm,深35 cm,箱中水面高10 cm。放入一个棱长为
20 cm的正方体铁块后,铁块顶部仍高于水面。这时水面上升了多少厘米?
铁块放入后,该长方体水箱可以看成一个环形水箱,根据此时水箱底面积可求水面高度
40×30×10÷(40×30-20×20)-10=5(cm)
答:这时水面上升了5 cm。
用“公式法”求体积
技 巧 3
5.一个长方体的表面积是67.92 dm2,底面积是19 dm2,底面周长是17.6 dm,这个长方体的体积是多少立方分米?
表面积-底面积×2=侧面积,
侧面积÷底面周长=高,
底面积×高=体积。
67.92-19×2=29.92(dm2)
29.92÷17.6=1.7(dm)
19×1.7=32.3(dm3)
答:这个长方体的体积是32.3 dm3。
用“操作法”求容积
技 巧 4
6.用一张长40 cm、宽20 cm的铁皮做一个深5 cm的无盖铁皮盒子,怎样做能使铁皮盒子的容积最大?并求出最大容积。(请画图表示制作方法)
(40-5×4)×20×5=2000(cm3)
答:最大容积是2000 cm3。
Thank you!
