1.4.1 有理数的乘法课件
文档属性
| 名称 | 1.4.1 有理数的乘法课件 |  | |
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-08 16:05:49 | ||
图片预览






文档简介
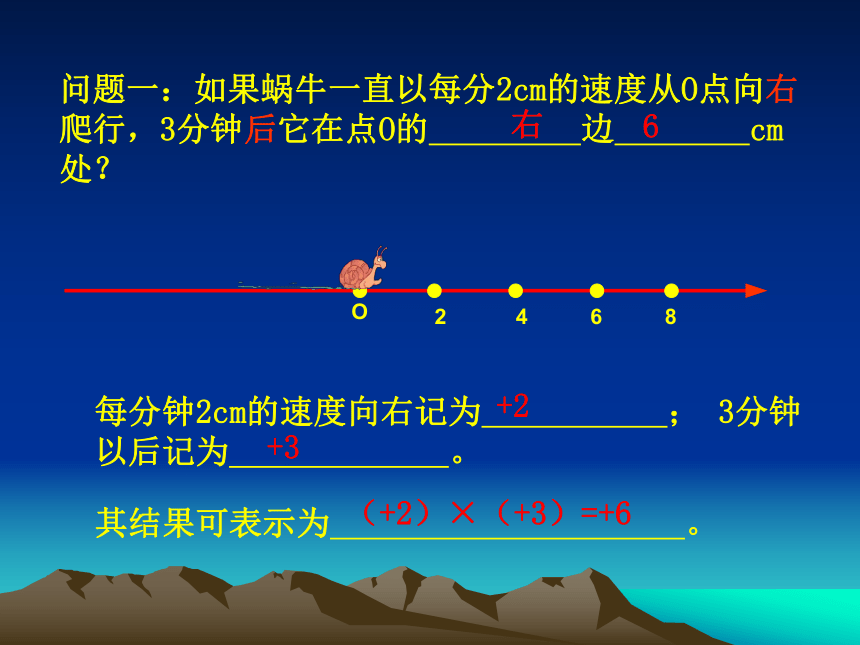
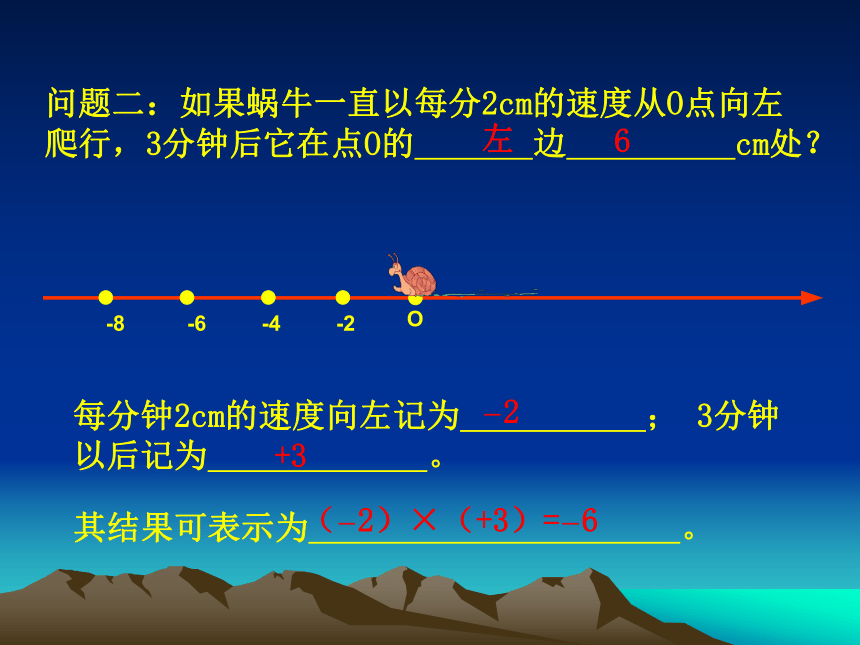
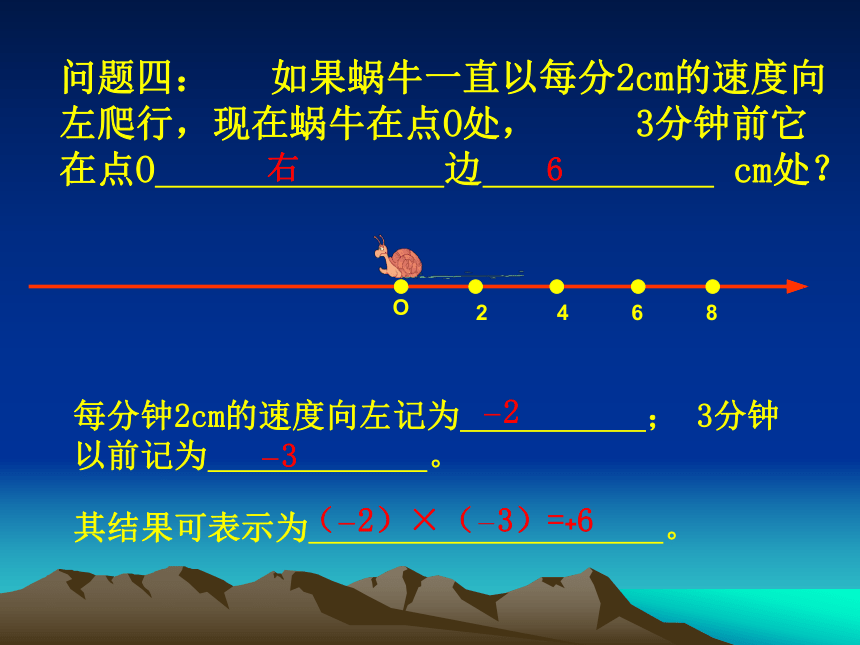
课件27张PPT。有理数的乘法授课人 刘启才lO如图,有一只蜗牛沿直线 l 爬行,它现在的位置恰好在l 上的一点O。2、如果3分钟以后记为+3分钟,那么3分钟以前应该记为 。 1、如果一只蜗牛向右爬行2cm记为+2cm,那么向左爬行2cm应该记为 。 -2cm-3分钟O问题一:如果蜗牛一直以每分2cm的速度从O点向右爬行,3分钟后它在点O的 边 cm处?+2+3(+2)×(+3)=+6问题二:如果蜗牛一直以每分2cm的速度从O点向左爬行,3分钟后它在点O的 边 cm处?O-8-6-4-2-2+3(-2)×(+3)=-6想一想:问题2的结果(-2)×(+3)=-6与问题1的结果(+2)×(+3)=+6有何区别?结论: 两个有理数相乘,改变其中一个因数的符号,积的符号也随之改变。问题三:如果蜗牛一直以每分2cm的速度向右爬行,现在蜗牛在点O处, 3分钟前它在点O的 边 cm处?O+2-3(+2)×(-3)=-6问题四: 如果蜗牛一直以每分2cm的速度向 左爬行,现在蜗牛在点O处, 3分钟前它在点O 边 cm处?O-2-3(-2)×(-3)=+6想一想:问题4的结果(-2)×(-3)=+6与问题1的结果(+2)×(+3)=+6有何区别?结论: 两个有理数相乘,同时改变两个因数的符号,积的符号不变。(+2)×(+3) = +6(-2)×(+3)= -6(+2)×(-3)= -6(-2)×(-3)= +6正数乘以正数积为 数负数乘以正数积为 数正数乘以负数积为 数负数乘以负数积为 数乘积的绝对值等于各因数绝对值的 。规律呈现:正负负正积问题五:如果蜗牛一直以每分钟2cm的速度向右爬行,0分钟后它在什么位置?O结论: 2×0= 0结论: 0×(-3)= 0乘法算式因数特征积的特征(-2)×(-3)=+6(+2)×(+3)=+6(+2)×(-3)=-6(-2)×(+3)=-6(+2)×0=00×(-3)=0同号异号一个因数为0得正得负得 0归纳有理数的乘法法则: 1、 两数相乘,同号得正,异号
得负,并把绝对值相乘。 2、任何数同零相乘,都得零。例如, (-5)×(-3),……
(-5)×(-3)= +(),……
5 × 3=15,…………
所以 (-5)×(-3)=15
又如,(-7) ×4,…………
(-7) ×4= -(),……
7 ×4=28,…………
所以 (-7) ×4=
有理数相乘,先确定积的 , 再确定
积的 。同号两数相乘得正把绝对值相乘异号两数相乘得负把绝对值相乘-28符号绝对值法则的应用:(-5)×(-3)(-7)×4= += 15(5 × 3)= -(7 × 4)= -28有理数相乘,先确定积的符号,再确定积的绝对值。例1 计算:(1)(-3) × 9(2)(- )×(-2)解:(1)(-3) × 9 = -(3 × 9 ) = -27(2)(- )×(-2)= +( × 2 )= 1小试牛刀(1) 6 × (- 9)(3)(- 6)×(- 1)(4)(- 6)× 0(2)(- 15) ×(5) 4 ×(6) ×(7)(- 12)×(- )(8)(- 2 )×(- )结论:乘积是1的两个数互为倒数1-13-3-3-3 例2:
用正负数表示气温的变化量,上升为正,
下降为负,登山队攀登一座山峰,每登高
1km气温的变化量为-6 0C,攀登3km后,
气温有什么变化?商店降价销售某种商品,每件降5元,
售出60件后,与按原价销售同样数量
的商品相比,销售额有什么变化?解:(-5)×60 =-300
答:销售额减少300元。再试牛刀三思而行(1) 若 ab>0,则必有 ( )A. a>0,b>0 B. a<0,b<0
C. a>0,b<0 D. a>0,b>0或a<0,b<0(2)若ab=0,则一定有( ) a=b=0 B. a,b至少有一个为0
C. a=0 D. a,b最多有一个为0DB(3)一个有理数和它的相反数之积( )A. 必为正数 B. 必为负数
C. 一定不大于零 D. 一定等于1(4)若ab=|ab|,则必有( ) a与b同号 B. a与b异号
C. a与b中至少有一个等于0 D. 以上都不对CD三思而行百尺竿头(2) | 2.5| ×[ ( )]数学游戏:在整数-5、-3、-1、2、4、6中任取两个数相乘,所得积的最大值与最小值分别是多少? 通过本节课的学习,大家有
什么收获呢?
作业: 1、习题1.5 第1题,
2、练习p31 第2题. 3、预习多个有理数相乘的乘法运算七四班同门再见七四班同学们再见2013年9月8日
得负,并把绝对值相乘。 2、任何数同零相乘,都得零。例如, (-5)×(-3),……
(-5)×(-3)= +(),……
5 × 3=15,…………
所以 (-5)×(-3)=15
又如,(-7) ×4,…………
(-7) ×4= -(),……
7 ×4=28,…………
所以 (-7) ×4=
有理数相乘,先确定积的 , 再确定
积的 。同号两数相乘得正把绝对值相乘异号两数相乘得负把绝对值相乘-28符号绝对值法则的应用:(-5)×(-3)(-7)×4= += 15(5 × 3)= -(7 × 4)= -28有理数相乘,先确定积的符号,再确定积的绝对值。例1 计算:(1)(-3) × 9(2)(- )×(-2)解:(1)(-3) × 9 = -(3 × 9 ) = -27(2)(- )×(-2)= +( × 2 )= 1小试牛刀(1) 6 × (- 9)(3)(- 6)×(- 1)(4)(- 6)× 0(2)(- 15) ×(5) 4 ×(6) ×(7)(- 12)×(- )(8)(- 2 )×(- )结论:乘积是1的两个数互为倒数1-13-3-3-3 例2:
用正负数表示气温的变化量,上升为正,
下降为负,登山队攀登一座山峰,每登高
1km气温的变化量为-6 0C,攀登3km后,
气温有什么变化?商店降价销售某种商品,每件降5元,
售出60件后,与按原价销售同样数量
的商品相比,销售额有什么变化?解:(-5)×60 =-300
答:销售额减少300元。再试牛刀三思而行(1) 若 ab>0,则必有 ( )A. a>0,b>0 B. a<0,b<0
C. a>0,b<0 D. a>0,b>0或a<0,b<0(2)若ab=0,则一定有( ) a=b=0 B. a,b至少有一个为0
C. a=0 D. a,b最多有一个为0DB(3)一个有理数和它的相反数之积( )A. 必为正数 B. 必为负数
C. 一定不大于零 D. 一定等于1(4)若ab=|ab|,则必有( ) a与b同号 B. a与b异号
C. a与b中至少有一个等于0 D. 以上都不对CD三思而行百尺竿头(2) | 2.5| ×[ ( )]数学游戏:在整数-5、-3、-1、2、4、6中任取两个数相乘,所得积的最大值与最小值分别是多少? 通过本节课的学习,大家有
什么收获呢?
作业: 1、习题1.5 第1题,
2、练习p31 第2题. 3、预习多个有理数相乘的乘法运算七四班同门再见七四班同学们再见2013年9月8日
