数学人教A版(2019)必修第一册4.1.2 无理数指数幂及其运算性质 课件(共14张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.1.2 无理数指数幂及其运算性质 课件(共14张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-13 07:00:45 | ||
图片预览




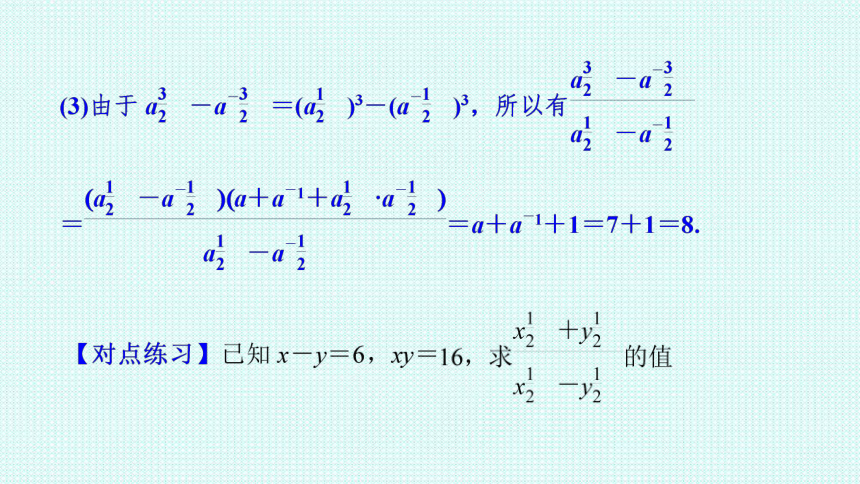
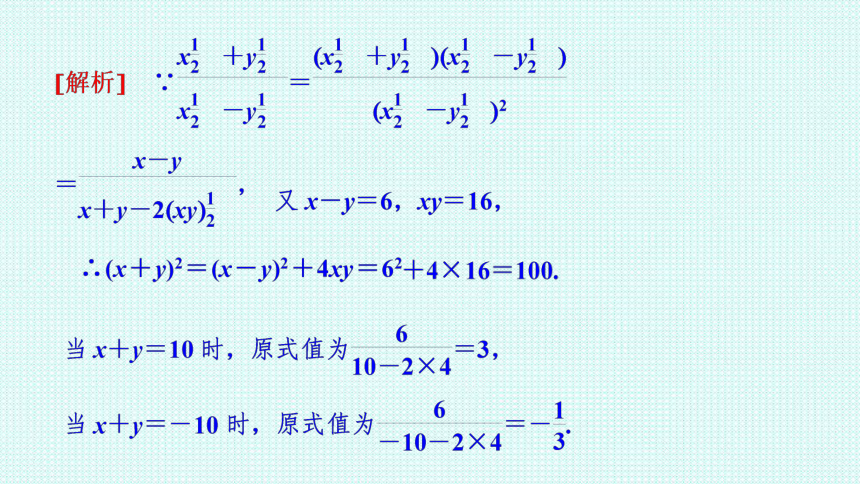
文档简介
(共14张PPT)
无理数指数幂及其运算性质
新课程标准 核心素养
1.无理数指数幂的概念; 数学抽象
2.实数指数幂和根式之间的互化; 逻辑推理
3.利用实数指数幂的运算性质化简求值; 数学运算
4.分析已知条件与所求式子之间的联系; 数据分析
5.通过与有理数指数幂性质进行类比,得出无理数指数幂的概念和性质. 数学建模
知识点一 无理数指数幂
一般地,无理数指数幂aα(a>0,α是无理数)是一个确定的实数.
知识点二 实数指数幂的运算性质
题型一 无理数指数幂的运算
a
π
6
2π
3
π
+
-
a
π
6
-
2
2
3
题型二 指数幂运算的综合应用
例 2
+ = 3
a
a
1
2
1
2
-
两边平方,得a+a-1+2=9,
a
1
a
由 ,a<0,
a
1
a
=
a
a2
a
=
a
解:原式=1+ 1 =0
2
2
10 =(10 ) = = =
2
3x-y
2
1
3x-y
10
10
y
3x
3
8
3
6
2
原式.
2
5
2
2
2
·
=
2
4
2
5
·
=
2
20
=( 2×2 ) =( 2 )
1
2
1
3
3
2
1
3
3
2
8
2
2
2
2
2
2
·
= =1
2
2
2
2
2
a
=m,
2=m
1
a
=m
5
b
5=m
1
b
10=m
1
a
1
b
+
α+β= -2, αβ=
1
5
1
4
2
1
5
3+2 =( +1)2
2
2
6-4 =(2- )2
2
2
原式=.
6-4
2
原式=2-.
2
无理数指数幂及其运算性质
新课程标准 核心素养
1.无理数指数幂的概念; 数学抽象
2.实数指数幂和根式之间的互化; 逻辑推理
3.利用实数指数幂的运算性质化简求值; 数学运算
4.分析已知条件与所求式子之间的联系; 数据分析
5.通过与有理数指数幂性质进行类比,得出无理数指数幂的概念和性质. 数学建模
知识点一 无理数指数幂
一般地,无理数指数幂aα(a>0,α是无理数)是一个确定的实数.
知识点二 实数指数幂的运算性质
题型一 无理数指数幂的运算
a
π
6
2π
3
π
+
-
a
π
6
-
2
2
3
题型二 指数幂运算的综合应用
例 2
+ = 3
a
a
1
2
1
2
-
两边平方,得a+a-1+2=9,
a
1
a
由 ,a<0,
a
1
a
=
a
a2
a
=
a
解:原式=1+ 1 =0
2
2
10 =(10 ) = = =
2
3x-y
2
1
3x-y
10
10
y
3x
3
8
3
6
2
原式.
2
5
2
2
2
·
=
2
4
2
5
·
=
2
20
=( 2×2 ) =( 2 )
1
2
1
3
3
2
1
3
3
2
8
2
2
2
2
2
2
·
= =1
2
2
2
2
2
a
=m,
2=m
1
a
=m
5
b
5=m
1
b
10=m
1
a
1
b
+
α+β= -2, αβ=
1
5
1
4
2
1
5
3+2 =( +1)2
2
2
6-4 =(2- )2
2
2
原式=.
6-4
2
原式=2-.
2
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
