人教版九年级上册24.2.1点和圆的位置关系 (第一课时) 课件(共19张PPT)
文档属性
| 名称 | 人教版九年级上册24.2.1点和圆的位置关系 (第一课时) 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 963.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 16:35:19 | ||
图片预览




文档简介
(共19张PPT)
第二十四章 圆
24.2.1 点和圆的位置关系
(第一课时)
人教版 九年级上册
学习目标
1.理解点和圆的三种位置关系
2.点和圆的三种位置关系解决一些实际问题
3.结合本节内容的学习,体会数形结合、分类讨论的数学思想.
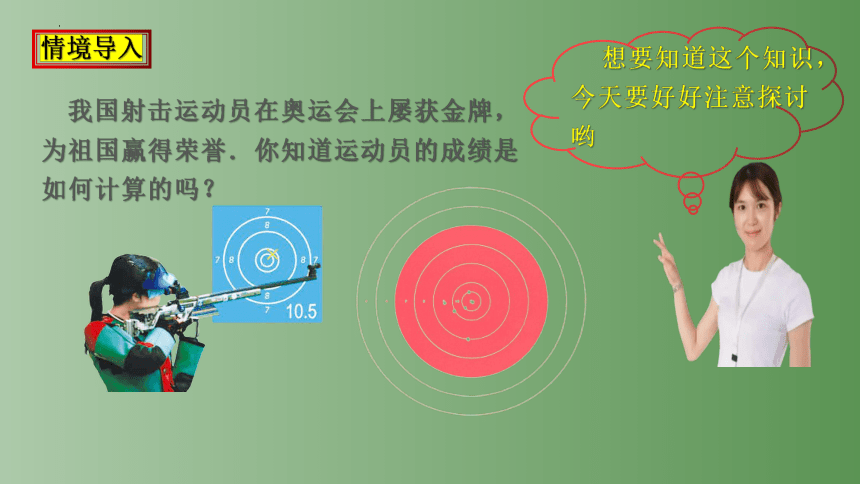
我国射击运动员在奥运会上屡获金牌,为祖国赢得荣誉.你知道运动员的成绩是如何计算的吗?
情境导入
想要知道这个知识,今天要好好注意探讨哟
如图,设⊙O 的半径为r
0
A
B
C
r
新知探究
则 OA<r
1.如图A点在圆内,
2.如图B点在圆上,
则 OB=r
则 OC>r
3.如图C点在圆外,
如图,设⊙O 的半径为r
点A在⊙O内
点B在⊙O上
点C在⊙O外
反过来也成立,如果已知点到圆心的距离和圆的半径的关系,就可以判断点和圆的位置关系.
OA<r
OB=r
OC>r
A
B
C
r
0
新知探究
圆外的点
圆内的点
圆上的点
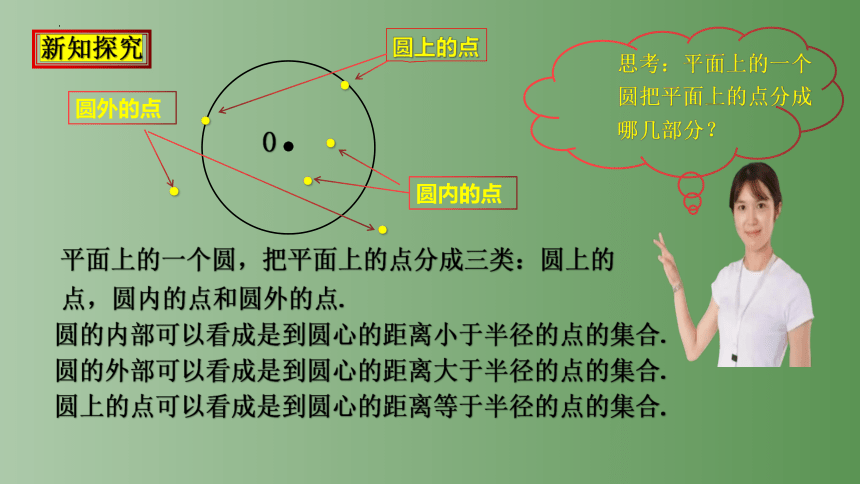
平面上的一个圆,把平面上的点分成三类:圆上的点,圆内的点和圆外的点.
圆的内部可以看成是到圆心的距离小于半径的点的集合.
圆的外部可以看成是到圆心的距离大于半径的点的集合.
圆上的点可以看成是到圆心的距离等于半径的点的集合.
新知探究
思考:平面上的一个圆把平面上的点分成哪几部分?
0
.
.
.
.
.
.
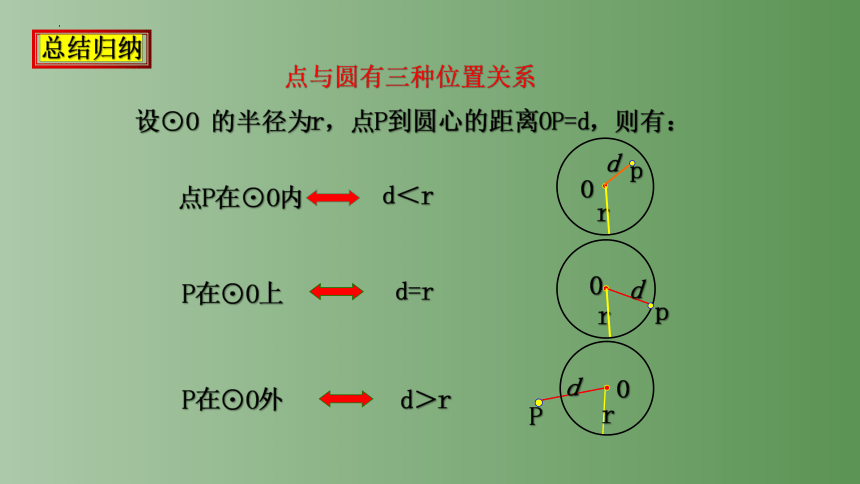
设⊙O 的半径为r,点P到圆心的距离OP=d,则有:
点P在⊙O内
P在⊙O上
P在⊙O外
d<r
d=r
d>r
点与圆有三种位置关系
p
r
d
0
p
r
d
0
P
r
d
0
总结归纳
你知道击中靶上不同位置的成绩是如何计算的吗 ?
射击靶图上,有一组以靶心为圆心的大小不同的圆,他们把靶图由内到外分成几个区域.
这些区域用由高到底的环数来表示,射击成绩
用弹着点位置对应的环数来表示.
弹着点与靶心的距离决定了它在哪个圆内,弹着点离靶心越近,它所在的区域就越靠内,对应的环数也就越高,射击的成绩越好.
解决问题
如图已知矩形ABCD的边AB=3厘米,AD=4厘米
A
D
C
B
(1)以点A为圆心,3厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
B在圆上,
D在圆外,
C在圆外
解:
例题分析
(2)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
A
D
C
B
解:B在圆内,
D在圆上,
C在圆外
如图已知矩形ABCD的边AB=3厘米,AD=4厘米
例题分析
(3)以点A为圆心,5厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
解:B在圆内
D在圆内
C在圆上
A
D
C
B
如图已知矩形ABCD的边AB=3厘米,AD=4厘米
例题分析
如图所示,已知⊙O 和直线l,过圆心O 作OP⊥l,P 为垂足,A,B,C为直线l上三个点,且PA=2cm,PB =3cm,PC =4cm,若⊙O的半径为5cm,OP=4cm,判断A,B,C三点与⊙O的位置关系.
点A在_________.
点B在_________.
点C在_________.
圆内
圆上
圆外
跟踪练习
课堂小结
点和圆的位置关系有三种:
设⊙O的半径为r,点P到圆心的距离为d,则
d<r
点P在圆外
点P在圆内
点P在圆上
p
r
d
0
p
r
d
0
d=r
d>r
r
P
d
0
1.若圆O的半径为4,OA=6,则符合题意的图形可能是( )
当堂检测
2.有一张矩形纸片,AB =3cm,AD =4cm,若以A为圆心作圆,并且要使点D 在⊙A内,而点C 在⊙A外, ⊙A的半径 r 的取值范围是__________________.
当堂检测
3.⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:
点A在___ _;点B在_____;点C在______ .
当堂检测
4.⊙O的半径6cm,
(1)当OP=6时,点P在____________;
(2)当OP___________时,点P在圆内;
(3)当OP___________时,点P不在圆外.
当堂检测
5.如图,已知△ABC中,∠C=90°,AC=3,BC=4,以点C为圆心作⊙C,半径为r.
(1)当r取什么值时,点A在⊙C外?
(2)当r取什么值时,点A在⊙C内,点B在⊙C外.
当堂检测
坚持就是胜利
第二十四章 圆
24.2.1 点和圆的位置关系
(第一课时)
人教版 九年级上册
学习目标
1.理解点和圆的三种位置关系
2.点和圆的三种位置关系解决一些实际问题
3.结合本节内容的学习,体会数形结合、分类讨论的数学思想.
我国射击运动员在奥运会上屡获金牌,为祖国赢得荣誉.你知道运动员的成绩是如何计算的吗?
情境导入
想要知道这个知识,今天要好好注意探讨哟
如图,设⊙O 的半径为r
0
A
B
C
r
新知探究
则 OA<r
1.如图A点在圆内,
2.如图B点在圆上,
则 OB=r
则 OC>r
3.如图C点在圆外,
如图,设⊙O 的半径为r
点A在⊙O内
点B在⊙O上
点C在⊙O外
反过来也成立,如果已知点到圆心的距离和圆的半径的关系,就可以判断点和圆的位置关系.
OA<r
OB=r
OC>r
A
B
C
r
0
新知探究
圆外的点
圆内的点
圆上的点
平面上的一个圆,把平面上的点分成三类:圆上的点,圆内的点和圆外的点.
圆的内部可以看成是到圆心的距离小于半径的点的集合.
圆的外部可以看成是到圆心的距离大于半径的点的集合.
圆上的点可以看成是到圆心的距离等于半径的点的集合.
新知探究
思考:平面上的一个圆把平面上的点分成哪几部分?
0
.
.
.
.
.
.
设⊙O 的半径为r,点P到圆心的距离OP=d,则有:
点P在⊙O内
P在⊙O上
P在⊙O外
d<r
d=r
d>r
点与圆有三种位置关系
p
r
d
0
p
r
d
0
P
r
d
0
总结归纳
你知道击中靶上不同位置的成绩是如何计算的吗 ?
射击靶图上,有一组以靶心为圆心的大小不同的圆,他们把靶图由内到外分成几个区域.
这些区域用由高到底的环数来表示,射击成绩
用弹着点位置对应的环数来表示.
弹着点与靶心的距离决定了它在哪个圆内,弹着点离靶心越近,它所在的区域就越靠内,对应的环数也就越高,射击的成绩越好.
解决问题
如图已知矩形ABCD的边AB=3厘米,AD=4厘米
A
D
C
B
(1)以点A为圆心,3厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
B在圆上,
D在圆外,
C在圆外
解:
例题分析
(2)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
A
D
C
B
解:B在圆内,
D在圆上,
C在圆外
如图已知矩形ABCD的边AB=3厘米,AD=4厘米
例题分析
(3)以点A为圆心,5厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
解:B在圆内
D在圆内
C在圆上
A
D
C
B
如图已知矩形ABCD的边AB=3厘米,AD=4厘米
例题分析
如图所示,已知⊙O 和直线l,过圆心O 作OP⊥l,P 为垂足,A,B,C为直线l上三个点,且PA=2cm,PB =3cm,PC =4cm,若⊙O的半径为5cm,OP=4cm,判断A,B,C三点与⊙O的位置关系.
点A在_________.
点B在_________.
点C在_________.
圆内
圆上
圆外
跟踪练习
课堂小结
点和圆的位置关系有三种:
设⊙O的半径为r,点P到圆心的距离为d,则
d<r
点P在圆外
点P在圆内
点P在圆上
p
r
d
0
p
r
d
0
d=r
d>r
r
P
d
0
1.若圆O的半径为4,OA=6,则符合题意的图形可能是( )
当堂检测
2.有一张矩形纸片,AB =3cm,AD =4cm,若以A为圆心作圆,并且要使点D 在⊙A内,而点C 在⊙A外, ⊙A的半径 r 的取值范围是__________________.
当堂检测
3.⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:
点A在___ _;点B在_____;点C在______ .
当堂检测
4.⊙O的半径6cm,
(1)当OP=6时,点P在____________;
(2)当OP___________时,点P在圆内;
(3)当OP___________时,点P不在圆外.
当堂检测
5.如图,已知△ABC中,∠C=90°,AC=3,BC=4,以点C为圆心作⊙C,半径为r.
(1)当r取什么值时,点A在⊙C外?
(2)当r取什么值时,点A在⊙C内,点B在⊙C外.
当堂检测
坚持就是胜利
同课章节目录
