全等三角形的复习
图片预览


文档简介
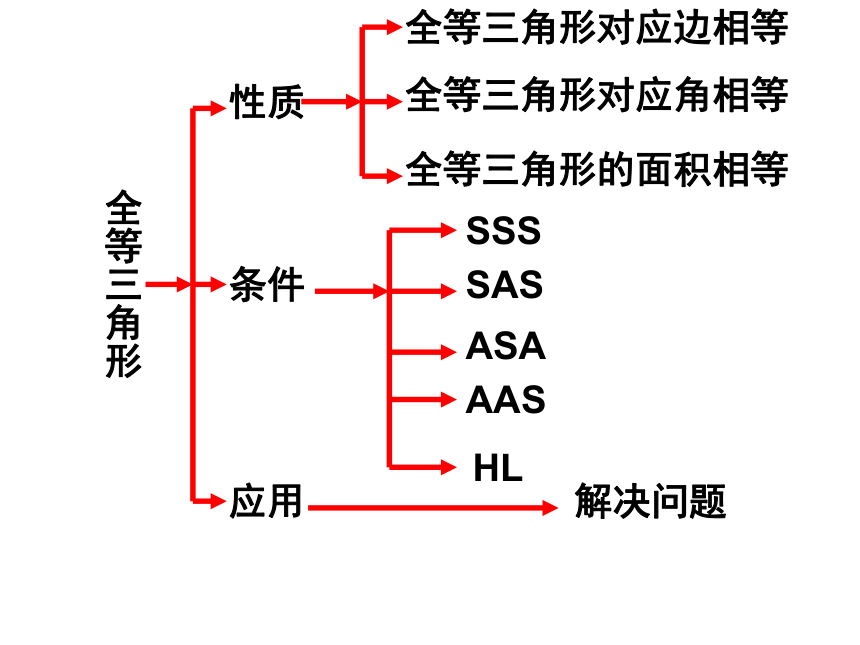
课件23张PPT。11.全等三角形复习课全等三角形性质条件应用全等三角形对应边相等全等三角形对应角相等全等三角形的面积相等SSSSASASAAASHL解决问题角平分线的性质角平分线上的点到角两边的距离相等。
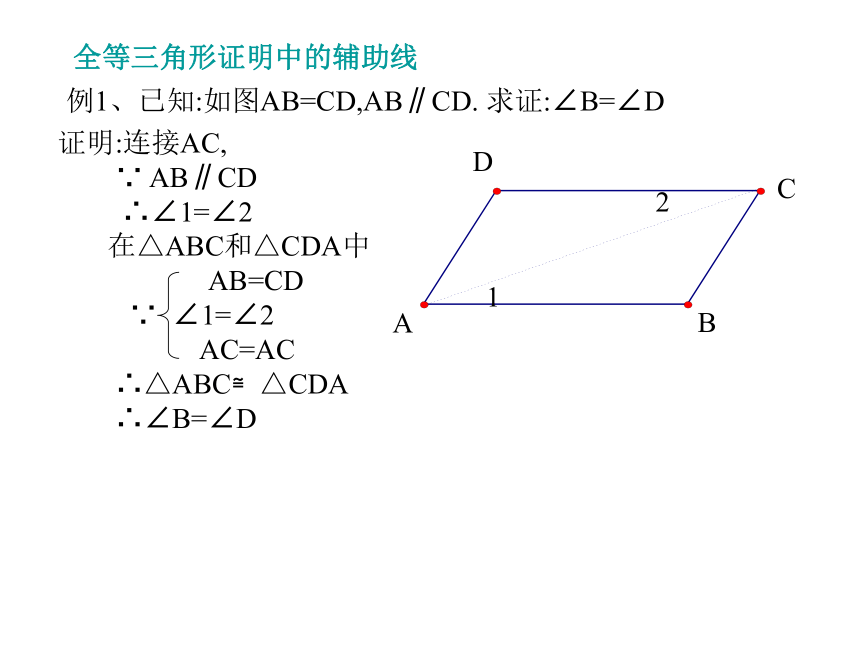
角的内部到角两边距离相等的点在角的平分线上例1、已知:如图AB=CD,AB∥CD. 求证:∠B=∠DABCD证明:连接AC,
∵ AB∥CD
∴∠1=∠2
在△ABC和△CDA中
AB=CD
∵ ∠1=∠2
AC=AC
∴△ABC≌△CDA
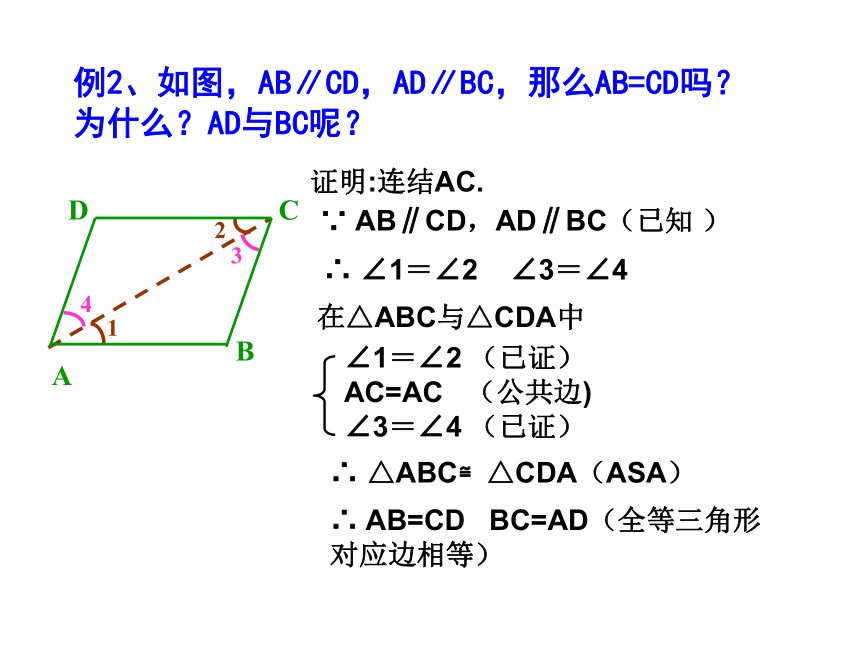
∴∠B=∠D12全等三角形证明中的辅助线∵ AB∥CD,AD∥BC(已知 )∴ ∠1=∠2 ∠3=∠4
在△ABC与△CDA中
∠1=∠2 (已证)
AC=AC (公共边)
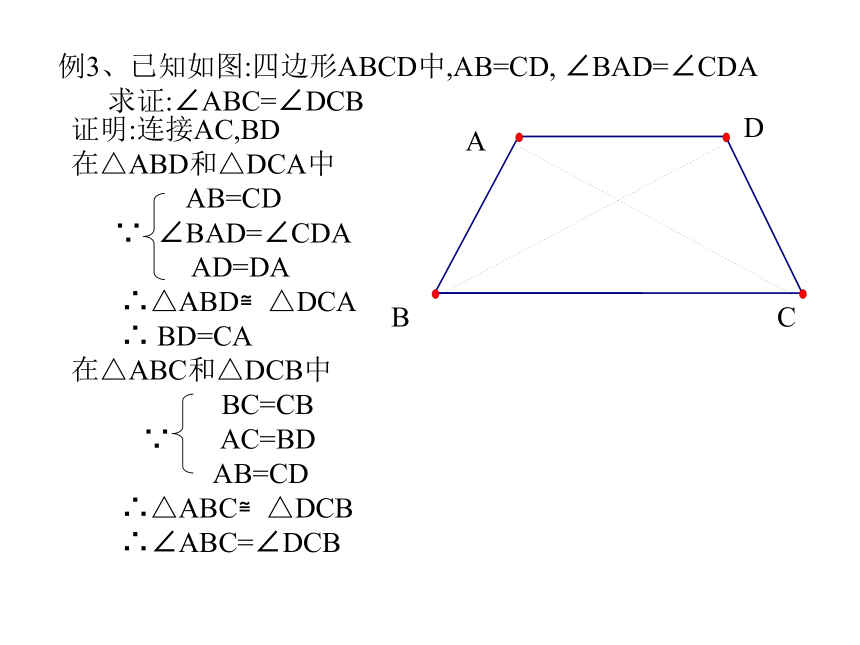
∠3=∠4 (已证)∴ △ABC≌△CDA(ASA)∴ AB=CD BC=AD(全等三角形对应边相等)证明:连结AC.例2、如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?ABCD2341例3、已知如图:四边形ABCD中,AB=CD, ∠BAD=∠CDA
求证:∠ABC=∠DCBBADC证明:连接AC,BD
在△ABD和△DCA中
AB=CD
∵ ∠BAD=∠CDA
AD=DA
∴△ABD≌△DCA
∴ BD=CA
在△ABC和△DCB中
BC=CB
∵ AC=BD
AB=CD
∴△ABC≌△DCB
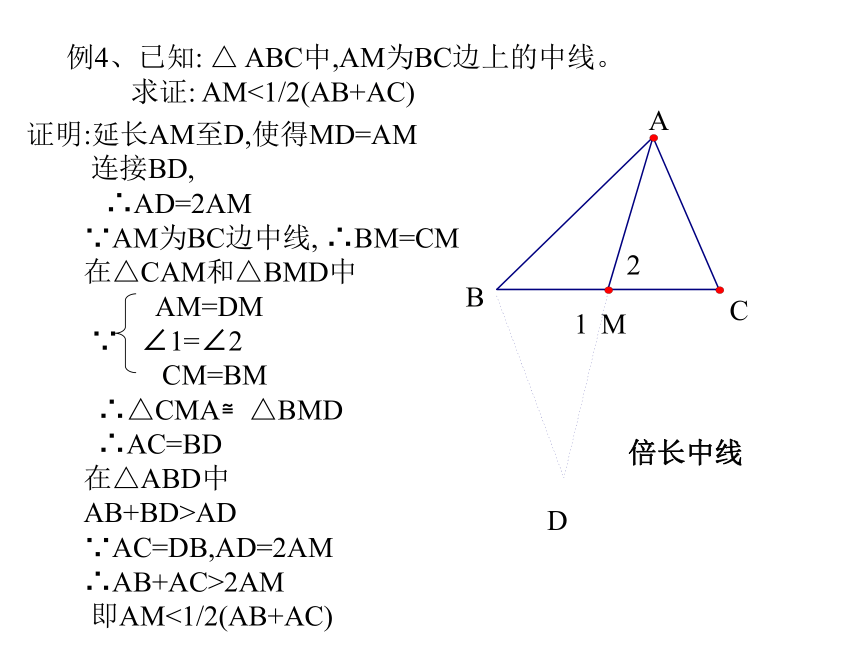
∴∠ABC=∠DCB例4、已知: △ ABC中,AM为BC边上的中线。
求证: AM<1/2(AB+AC)ABCMD证明:延长AM至D,使得MD=AM
连接BD,
∴AD=2AM
∵AM为BC边中线, ∴BM=CM
在△CAM和△BMD中
AM=DM
∵ ∠1=∠2
CM=BM
∴△CMA≌△BMD
∴AC=BD
在△ABD中
AB+BD>AD
∵AC=DB,AD=2AM
∴AB+AC>2AM
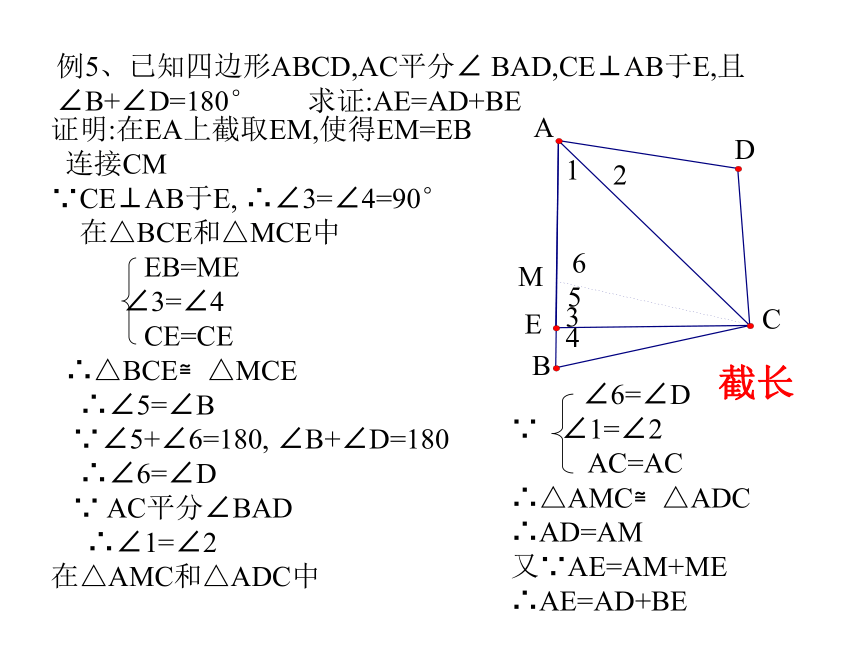
即AM<1/2(AB+AC)12倍长中线例5、已知四边形ABCD,AC平分∠ BAD,CE⊥AB于E,且
∠B+∠D=180° 求证:AE=AD+BEABEDCM证明:在EA上截取EM,使得EM=EB
连接CM
∵CE⊥AB于E, ∴∠3=∠4=90°
在△BCE和△MCE中
EB=ME
∠3=∠4
CE=CE
∴△BCE≌△MCE
∴∠5=∠B
∵∠5+∠6=180, ∠B+∠D=180
∴∠6=∠D
∵ AC平分∠BAD
∴∠1=∠2
在△AMC和△ADC中
∠6=∠D
∵ ∠1=∠2
AC=AC
∴△AMC≌△ADC
∴AD=AM
又∵AE=AM+ME
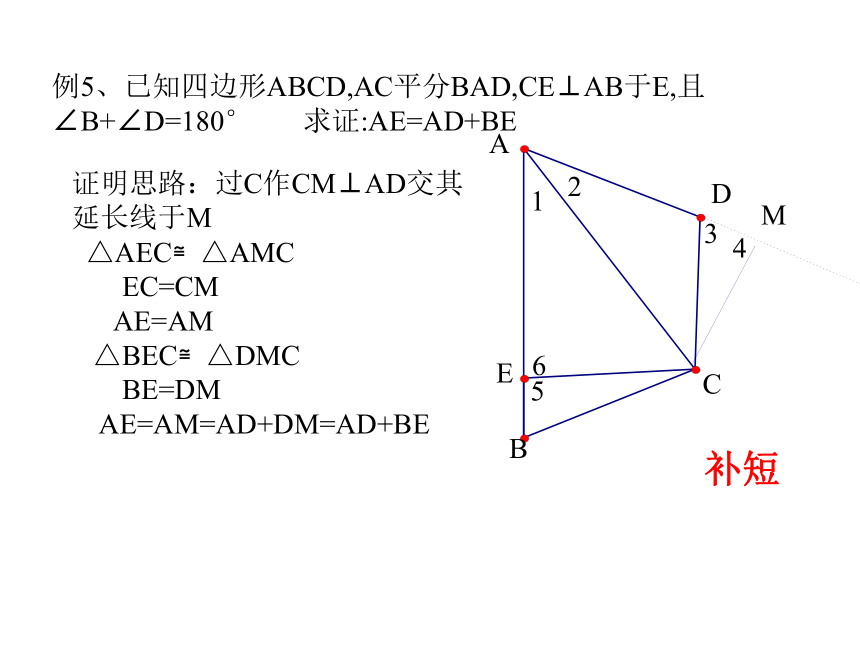
∴AE=AD+BE123456截长ABCDEM125634证明思路:过C作CM⊥AD交其
延长线于M
△AEC≌△AMC
EC=CM
AE=AM
△BEC≌△DMC
BE=DM
AE=AM=AD+DM=AD+BE
例5、已知四边形ABCD,AC平分BAD,CE⊥AB于E,且
∠B+∠D=180° 求证:AE=AD+BE补短小结:1)一般情况:
2)倍长中线
3)截长补短
全等三角形 ⑷证明两个三角形全等,要结合题目的条件和结论,选择恰当方法
⑸全等三角形,是证明两条线段或两个角相等的重要方法之一,证明时
①要观察待证的线段或角,在哪两个可能全等的三角形中。
②分析要证两个三角形全等,已有什么条件,还缺什么条件。
③有公共边的,公共边一定是对应边, 有公共角的,公共角一定是对应角,有对顶角,对顶角也是对应角
④设法证明所缺的条件,有时所缺的条件可能在另一对全等三角形中,必须证两次全等。
⑤当要证的相等线段或角分别在两组以上的可能全等的三角形中,就应分析证明哪对三角形全等最好,一般选择条件具备多的一对较简单。
⑹有时证两线段相等,如存在角平分线且存在角平分线上的点到角的两边的垂线段就可直接用角平分线的性质定理来证,而不要去证三角形全等。 总之,证明过程中能用简单方法的就不要绕弯路。 CBA1、 如图:△ABC≌△ABD,且AC=AD,用等式写出这两个三角形的其它对应边和对应角。 公共边为对应边2、 如图:已知△ABD≌△ACE,且AB=AC,用等式写出两个三角形的其它对应边和对应角。
公共角为对应角ABDEC3、 如图△ABC≌△EDC,∠A=∠E,用等式写出两个三角形其它的对应角和对应边。
对顶角为对应角找全等三角形对应边和对应角的方法:1、从长短大小两个全等三角形的一对最长边(最大角)是对应边(角);一对最短边(最小角)是对应边(角)2、从对应边与对应角的关系对应角所对的边为对应边;对应边所对的角为对应角;两个对应角所夹的边为对应边;两条对应边所夹的角为对应角。3、从位置公共边为对应边;公共角为对应角;对顶角为对应角应用一、∵△ABC≌ △DFE
∴ AB=DF, BC=FE, AC=DE
( )
∴ ∠ A= ∠ D, ∠ B= ∠ F ,
∠ C= ∠ E
( )全等三角形的对应角相等全等三角形的对应边相等二、 已知如图△ABC≌△DFE,∠A=96o,∠B=25o,DF=10cm。
求 ∠E的度数及AB的长。
BACEDF寻找对应元素的规律
总结(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,最小的边是对应边;
(5)两个全等三角形最大的角是对应角,最小的角是 对应角;
复习知识与要点全等三角形的判定方法:(1)SAS:(2)AAS:(4)SSS:(3)ASA:(5)HL有两边和它们的夹角对应相等的两个三角形全等有两个角和其中一角的对边对应相等的
两个三角形全等有两个角和它们的夹边对应相等的两个
三角形全等三边对应相等的两个三角形全等有斜边和一条直角边对应相等的两个直角
三角形全等1。证明两个三角形全等,要结合题目的条件和结论,选择恰当的判定方法
2。全等三角形,是证明两条线段或两个角相等的重要方法之一,证明时
①要观察待证的线段或角,在哪两个可能全等的三角形中。
②分析要证的两个三角形全等,已有什么条件,还缺什么条件。
③有公共边的,公共边一定是对应边, 有公共角的,公共角一定是对应角,有对顶角,对顶角也是对应角
总之,证明过程中能用简单方法的就不要绕弯路。 基础训练1、判断下面各组的两个三角形是否全等: (1) (2)已知:AB=CD, (3)已知:AC=AD,BC=BD
∠A=∠D(SAS) (AAS)(SSS)△ABC≌△DEF △AOB≌△DOC △ABC≌△ABD 基础训练(4)已知:AB=CD,AE=CF2、如图,下列条件,可以判定△ABC≌△DEF的是( )A、∠A=∠D,∠B=∠E,∠C=∠F
B、AB=DE,∠B=∠E,AC=DF
C、∠A=∠D,∠B=∠E,AC=DF (HL) △ABF≌△CDE C 基础训练 3、如图:已知AB=CD, AD=BC
则图中有( )组三角形全等。
A、2 B、3 C、4 D、5 4、如图:已知AC=AD,
只需附加一个条件,就能
使△ACB≌△ADB,请写
出一个符合的条件_____________。
△ABD≌ △CDB
△AOB≌ △COD△ADC≌△CBA
△AOD≌△COB
BC=BD 或(∠CAB=∠DAB) c
角的内部到角两边距离相等的点在角的平分线上例1、已知:如图AB=CD,AB∥CD. 求证:∠B=∠DABCD证明:连接AC,
∵ AB∥CD
∴∠1=∠2
在△ABC和△CDA中
AB=CD
∵ ∠1=∠2
AC=AC
∴△ABC≌△CDA
∴∠B=∠D12全等三角形证明中的辅助线∵ AB∥CD,AD∥BC(已知 )∴ ∠1=∠2 ∠3=∠4
在△ABC与△CDA中
∠1=∠2 (已证)
AC=AC (公共边)
∠3=∠4 (已证)∴ △ABC≌△CDA(ASA)∴ AB=CD BC=AD(全等三角形对应边相等)证明:连结AC.例2、如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?ABCD2341例3、已知如图:四边形ABCD中,AB=CD, ∠BAD=∠CDA
求证:∠ABC=∠DCBBADC证明:连接AC,BD
在△ABD和△DCA中
AB=CD
∵ ∠BAD=∠CDA
AD=DA
∴△ABD≌△DCA
∴ BD=CA
在△ABC和△DCB中
BC=CB
∵ AC=BD
AB=CD
∴△ABC≌△DCB
∴∠ABC=∠DCB例4、已知: △ ABC中,AM为BC边上的中线。
求证: AM<1/2(AB+AC)ABCMD证明:延长AM至D,使得MD=AM
连接BD,
∴AD=2AM
∵AM为BC边中线, ∴BM=CM
在△CAM和△BMD中
AM=DM
∵ ∠1=∠2
CM=BM
∴△CMA≌△BMD
∴AC=BD
在△ABD中
AB+BD>AD
∵AC=DB,AD=2AM
∴AB+AC>2AM
即AM<1/2(AB+AC)12倍长中线例5、已知四边形ABCD,AC平分∠ BAD,CE⊥AB于E,且
∠B+∠D=180° 求证:AE=AD+BEABEDCM证明:在EA上截取EM,使得EM=EB
连接CM
∵CE⊥AB于E, ∴∠3=∠4=90°
在△BCE和△MCE中
EB=ME
∠3=∠4
CE=CE
∴△BCE≌△MCE
∴∠5=∠B
∵∠5+∠6=180, ∠B+∠D=180
∴∠6=∠D
∵ AC平分∠BAD
∴∠1=∠2
在△AMC和△ADC中
∠6=∠D
∵ ∠1=∠2
AC=AC
∴△AMC≌△ADC
∴AD=AM
又∵AE=AM+ME
∴AE=AD+BE123456截长ABCDEM125634证明思路:过C作CM⊥AD交其
延长线于M
△AEC≌△AMC
EC=CM
AE=AM
△BEC≌△DMC
BE=DM
AE=AM=AD+DM=AD+BE
例5、已知四边形ABCD,AC平分BAD,CE⊥AB于E,且
∠B+∠D=180° 求证:AE=AD+BE补短小结:1)一般情况:
2)倍长中线
3)截长补短
全等三角形 ⑷证明两个三角形全等,要结合题目的条件和结论,选择恰当方法
⑸全等三角形,是证明两条线段或两个角相等的重要方法之一,证明时
①要观察待证的线段或角,在哪两个可能全等的三角形中。
②分析要证两个三角形全等,已有什么条件,还缺什么条件。
③有公共边的,公共边一定是对应边, 有公共角的,公共角一定是对应角,有对顶角,对顶角也是对应角
④设法证明所缺的条件,有时所缺的条件可能在另一对全等三角形中,必须证两次全等。
⑤当要证的相等线段或角分别在两组以上的可能全等的三角形中,就应分析证明哪对三角形全等最好,一般选择条件具备多的一对较简单。
⑹有时证两线段相等,如存在角平分线且存在角平分线上的点到角的两边的垂线段就可直接用角平分线的性质定理来证,而不要去证三角形全等。 总之,证明过程中能用简单方法的就不要绕弯路。 CBA1、 如图:△ABC≌△ABD,且AC=AD,用等式写出这两个三角形的其它对应边和对应角。 公共边为对应边2、 如图:已知△ABD≌△ACE,且AB=AC,用等式写出两个三角形的其它对应边和对应角。
公共角为对应角ABDEC3、 如图△ABC≌△EDC,∠A=∠E,用等式写出两个三角形其它的对应角和对应边。
对顶角为对应角找全等三角形对应边和对应角的方法:1、从长短大小两个全等三角形的一对最长边(最大角)是对应边(角);一对最短边(最小角)是对应边(角)2、从对应边与对应角的关系对应角所对的边为对应边;对应边所对的角为对应角;两个对应角所夹的边为对应边;两条对应边所夹的角为对应角。3、从位置公共边为对应边;公共角为对应角;对顶角为对应角应用一、∵△ABC≌ △DFE
∴ AB=DF, BC=FE, AC=DE
( )
∴ ∠ A= ∠ D, ∠ B= ∠ F ,
∠ C= ∠ E
( )全等三角形的对应角相等全等三角形的对应边相等二、 已知如图△ABC≌△DFE,∠A=96o,∠B=25o,DF=10cm。
求 ∠E的度数及AB的长。
BACEDF寻找对应元素的规律
总结(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,最小的边是对应边;
(5)两个全等三角形最大的角是对应角,最小的角是 对应角;
复习知识与要点全等三角形的判定方法:(1)SAS:(2)AAS:(4)SSS:(3)ASA:(5)HL有两边和它们的夹角对应相等的两个三角形全等有两个角和其中一角的对边对应相等的
两个三角形全等有两个角和它们的夹边对应相等的两个
三角形全等三边对应相等的两个三角形全等有斜边和一条直角边对应相等的两个直角
三角形全等1。证明两个三角形全等,要结合题目的条件和结论,选择恰当的判定方法
2。全等三角形,是证明两条线段或两个角相等的重要方法之一,证明时
①要观察待证的线段或角,在哪两个可能全等的三角形中。
②分析要证的两个三角形全等,已有什么条件,还缺什么条件。
③有公共边的,公共边一定是对应边, 有公共角的,公共角一定是对应角,有对顶角,对顶角也是对应角
总之,证明过程中能用简单方法的就不要绕弯路。 基础训练1、判断下面各组的两个三角形是否全等: (1) (2)已知:AB=CD, (3)已知:AC=AD,BC=BD
∠A=∠D(SAS) (AAS)(SSS)△ABC≌△DEF △AOB≌△DOC △ABC≌△ABD 基础训练(4)已知:AB=CD,AE=CF2、如图,下列条件,可以判定△ABC≌△DEF的是( )A、∠A=∠D,∠B=∠E,∠C=∠F
B、AB=DE,∠B=∠E,AC=DF
C、∠A=∠D,∠B=∠E,AC=DF (HL) △ABF≌△CDE C 基础训练 3、如图:已知AB=CD, AD=BC
则图中有( )组三角形全等。
A、2 B、3 C、4 D、5 4、如图:已知AC=AD,
只需附加一个条件,就能
使△ACB≌△ADB,请写
出一个符合的条件_____________。
△ABD≌ △CDB
△AOB≌ △COD△ADC≌△CBA
△AOD≌△COB
BC=BD 或(∠CAB=∠DAB) c
