12.3.1角平分线的性质(一)
文档属性
| 名称 | 12.3.1角平分线的性质(一) |  | |
| 格式 | zip | ||
| 文件大小 | 778.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-09 14:56:14 | ||
图片预览





文档简介
课件13张PPT。(1)八区一中 数学组 学习目标:
1.通过操作、验证等方式,
掌握角平分线的性质定理
2.能运用角的平分线性质定理
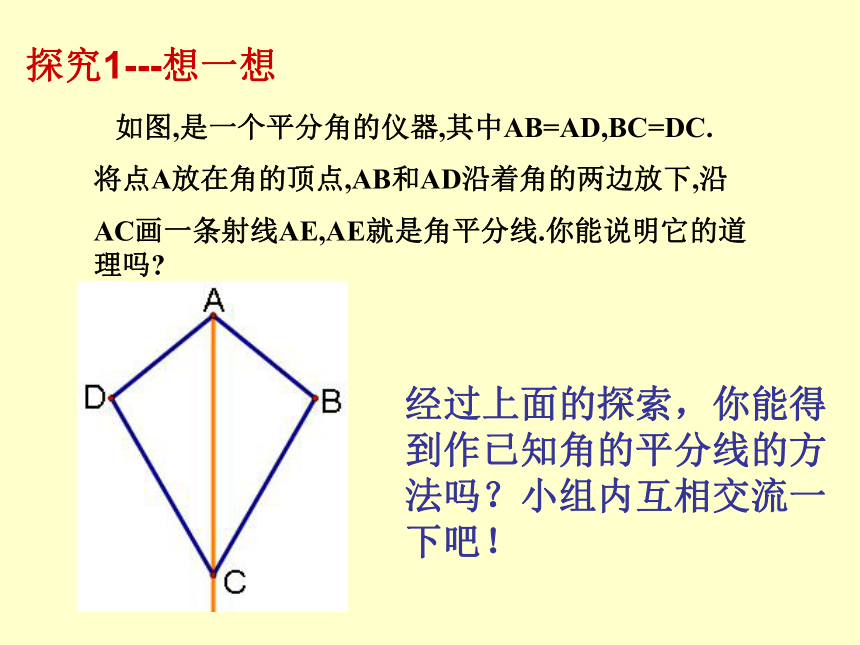
解决简单的几何问题. 下图中,能表示点P到直线l的距离的是线段PC的长 如图,是一个平分角的仪器,其中AB=AD,BC=DC.
将点A放在角的顶点,AB和AD沿着角的两边放下,沿
AC画一条射线AE,AE就是角平分线.你能说明它的道理吗?经过上面的探索,你能得到作已知角的平分线的方法吗?小组内互相交流一下吧!探究1---想一想AB作法:
⑴以O为圆心,任意长为半径作弧,交OA于M,交OB于N.
⑵分别以M,N为圆心,大于 的长为半径作弧,两弧在∠AOB的内部交于点C.
⑶作射线OC,
射线OC即为所求.0温馨提示:
作角平分线是最基本的尺规作图,大家一定要掌握噢!试一试 由上面的探究可以得出作已知角的平分线的方法 已知:∠AOB. 求作:∠AOB的平分线.请同学们拿出准备好的折纸与剪刀,自己动手:
1、剪一个角,
2、把剪好的角对折,使角的两边叠合在一起,再把纸片展开,你看到了什么?
3、把对折的纸片再任意折一次,然后 把纸片展开,又看到了什么?探究2---做一做(1)将∠ AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得到什么结论?OAB探究2---做一做(2) 已知:OC是∠AOB的平分线,点P在OC上,PD ⊥OA ,PE ⊥OB,垂足分别是D、E.
求证:PD=PE.证一证角平分线上的点到角的两边的距离相等你能用文字语言叙述一下发现的结论吗?说一说PD ⊥OA ,PE ⊥OB∵OP平分∠AOB∴PD=PE.用符号表示为:1、如图, △ABC的角平分线BM,CN相交于点P, 求证:点P到三边AB、BC、CA的距离相等证明:过点P作PD⊥AB于D,PE⊥BC于E,PF⊥AC于F
∴PD=PE 同理,PE=PF.
∴PD=PE=PF
即点P到三边AB、BC、CA的距离相等
用一用(1)已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.
求证:EB=FC. 温馨提示:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去. 用一用(2)丰收乐园回味无穷定理(文字语言): 角平分线上的点到这个角的两边的距离相等.
符号语言:
∵∠1=∠2 PD⊥OA,PE⊥OB(已知)
∴PD=PE(角平分线上的点到这个角的两边距离相等).
用尺规作角的平分线.
1.通过操作、验证等方式,
掌握角平分线的性质定理
2.能运用角的平分线性质定理
解决简单的几何问题. 下图中,能表示点P到直线l的距离的是线段PC的长 如图,是一个平分角的仪器,其中AB=AD,BC=DC.
将点A放在角的顶点,AB和AD沿着角的两边放下,沿
AC画一条射线AE,AE就是角平分线.你能说明它的道理吗?经过上面的探索,你能得到作已知角的平分线的方法吗?小组内互相交流一下吧!探究1---想一想AB作法:
⑴以O为圆心,任意长为半径作弧,交OA于M,交OB于N.
⑵分别以M,N为圆心,大于 的长为半径作弧,两弧在∠AOB的内部交于点C.
⑶作射线OC,
射线OC即为所求.0温馨提示:
作角平分线是最基本的尺规作图,大家一定要掌握噢!试一试 由上面的探究可以得出作已知角的平分线的方法 已知:∠AOB. 求作:∠AOB的平分线.请同学们拿出准备好的折纸与剪刀,自己动手:
1、剪一个角,
2、把剪好的角对折,使角的两边叠合在一起,再把纸片展开,你看到了什么?
3、把对折的纸片再任意折一次,然后 把纸片展开,又看到了什么?探究2---做一做(1)将∠ AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得到什么结论?OAB探究2---做一做(2) 已知:OC是∠AOB的平分线,点P在OC上,PD ⊥OA ,PE ⊥OB,垂足分别是D、E.
求证:PD=PE.证一证角平分线上的点到角的两边的距离相等你能用文字语言叙述一下发现的结论吗?说一说PD ⊥OA ,PE ⊥OB∵OP平分∠AOB∴PD=PE.用符号表示为:1、如图, △ABC的角平分线BM,CN相交于点P, 求证:点P到三边AB、BC、CA的距离相等证明:过点P作PD⊥AB于D,PE⊥BC于E,PF⊥AC于F
∴PD=PE 同理,PE=PF.
∴PD=PE=PF
即点P到三边AB、BC、CA的距离相等
用一用(1)已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.
求证:EB=FC. 温馨提示:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去. 用一用(2)丰收乐园回味无穷定理(文字语言): 角平分线上的点到这个角的两边的距离相等.
符号语言:
∵∠1=∠2 PD⊥OA,PE⊥OB(已知)
∴PD=PE(角平分线上的点到这个角的两边距离相等).
用尺规作角的平分线.
