1.4.2.正弦函数和余弦函数的性质
文档属性
| 名称 | 1.4.2.正弦函数和余弦函数的性质 |  | |
| 格式 | zip | ||
| 文件大小 | 34.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-09 21:23:28 | ||
图片预览



文档简介
课件9张PPT。正弦函数和余弦函数的性质(一) 下面我们研究正弦函数和余弦函数的主要性质.
1. 定义域:
正弦函数和余弦函数的定义域都是实数集 R,记作
y = sin x,x∈R,
y = cos x,x∈R,
其中 R 也可以换成(-∞,+∞).
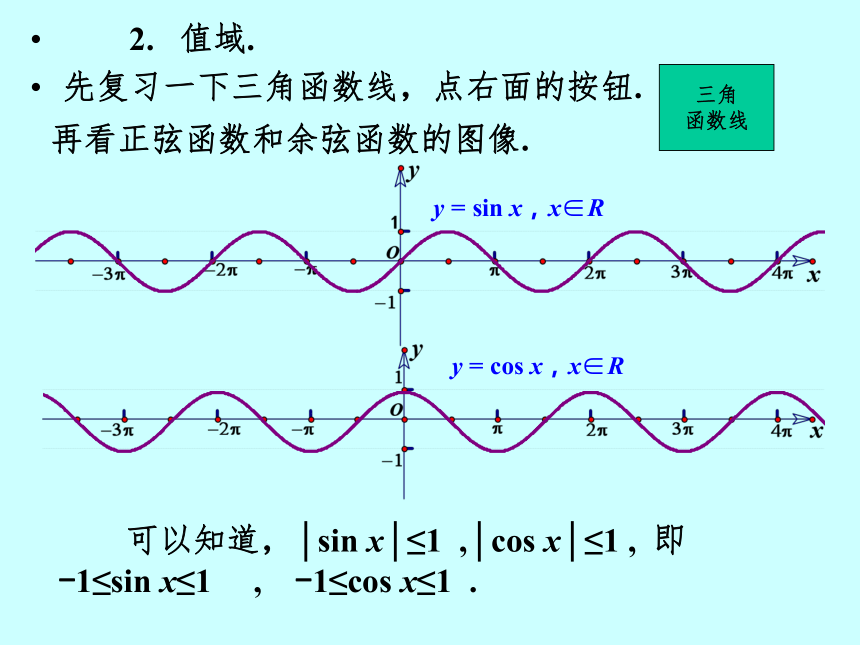
这也就是说,正弦和余弦符号后面的角可以取任意实数. 2. 值域.
先复习一下三角函数线,点右面的按钮.再看正弦函数和余弦函数的图像. 可以知道,│sin x│≤1 ,│cos x│≤1 , 即
-1≤sin x≤1 , -1≤cos x≤1 .三角
函数线 结论:正弦函数和余弦函数的值域
都是 [-1,1] .观察正弦曲线和余弦曲线,我们还可以发现,当 2kp < x < (2k+1)p (k∈Z) 时,sin x > 0 ;当 ( 2k -1 )p < x < 2kp (k∈Z) 时,sin x < 0 ; 3. 周期性
由诱导公式
sin (x + 2kp ) = sin x,cos ( x + 2kp ) = cos x (k∈Z)
可知,正弦函数值和余弦函数值的取得是有周期性的.
定义1:对于函数 f (x),如果存在一个非零常数 T,使得 当 x 取定义域内的每一个值时,都有
f ( x + T ) = f (x),
那么函数 f (x) 就叫做周期函数,非零常数 T 叫做这个函 数的周期.
定义2:对于一个周期函数 f (x),如果在它所有的周期中 存在一个最小的正数,那么这个最小正数就叫做 f (x)的最小 正周期.
结论:正弦函数和余弦函数都是周期函数,2kp (k∈Z且 k≠0) 都是它们的周期,最小正周期是2p. 注意:
(1) 根据周期函数的定义,如果 x∈周期函 数 f (x) 的定义域 M,则也有 x+T∈M,所以 当 T > 0 时,这个函数的定义域没有上界;当 T < 0 时,这个函数的定义域没有下界.
(2) 注意在定义1中的“每一个值”这几个字 是重要的,只要有一个值 x0 ,使得
f ( x0+T ) ≠ f (x0),
则 f (x) 就不是周期为 T 的周期函数.
(3) 如果不加特别说明,一般说到周期都 指的是最小正周期. 关于三角函数周期的一个重要结论: 例2 求使下列函数取得最大值的自变量 x 的集 合,并说出最大值是什么.
(1) y = cos x + 1,x∈R ;
(2) y = sin 2x ,x∈R . 思考:若把例2中的“最大值”改为“最小值”,
结果又将如何呢.
1. 定义域:
正弦函数和余弦函数的定义域都是实数集 R,记作
y = sin x,x∈R,
y = cos x,x∈R,
其中 R 也可以换成(-∞,+∞).
这也就是说,正弦和余弦符号后面的角可以取任意实数. 2. 值域.
先复习一下三角函数线,点右面的按钮.再看正弦函数和余弦函数的图像. 可以知道,│sin x│≤1 ,│cos x│≤1 , 即
-1≤sin x≤1 , -1≤cos x≤1 .三角
函数线 结论:正弦函数和余弦函数的值域
都是 [-1,1] .观察正弦曲线和余弦曲线,我们还可以发现,当 2kp < x < (2k+1)p (k∈Z) 时,sin x > 0 ;当 ( 2k -1 )p < x < 2kp (k∈Z) 时,sin x < 0 ; 3. 周期性
由诱导公式
sin (x + 2kp ) = sin x,cos ( x + 2kp ) = cos x (k∈Z)
可知,正弦函数值和余弦函数值的取得是有周期性的.
定义1:对于函数 f (x),如果存在一个非零常数 T,使得 当 x 取定义域内的每一个值时,都有
f ( x + T ) = f (x),
那么函数 f (x) 就叫做周期函数,非零常数 T 叫做这个函 数的周期.
定义2:对于一个周期函数 f (x),如果在它所有的周期中 存在一个最小的正数,那么这个最小正数就叫做 f (x)的最小 正周期.
结论:正弦函数和余弦函数都是周期函数,2kp (k∈Z且 k≠0) 都是它们的周期,最小正周期是2p. 注意:
(1) 根据周期函数的定义,如果 x∈周期函 数 f (x) 的定义域 M,则也有 x+T∈M,所以 当 T > 0 时,这个函数的定义域没有上界;当 T < 0 时,这个函数的定义域没有下界.
(2) 注意在定义1中的“每一个值”这几个字 是重要的,只要有一个值 x0 ,使得
f ( x0+T ) ≠ f (x0),
则 f (x) 就不是周期为 T 的周期函数.
(3) 如果不加特别说明,一般说到周期都 指的是最小正周期. 关于三角函数周期的一个重要结论: 例2 求使下列函数取得最大值的自变量 x 的集 合,并说出最大值是什么.
(1) y = cos x + 1,x∈R ;
(2) y = sin 2x ,x∈R . 思考:若把例2中的“最大值”改为“最小值”,
结果又将如何呢.
