2022-2023学年北师大版八年级数学上册 4.4 一次函数的应用 同步练习 (Word版含答案)
文档属性
| 名称 | 2022-2023学年北师大版八年级数学上册 4.4 一次函数的应用 同步练习 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 181.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 17:16:49 | ||
图片预览


文档简介
(北师大版)八年级上册 4.4 一次函数的应用 同步练习
一、单选题
1.某种出租车收费标准是:起步价7元(即行驶距离不超过3千米需付7元车费),超过了3千米以后,每增加1千米加收2.4元(不足1千米按1千米计),某人乘这种出租车从甲地到乙地支付车费19元,设此人从甲地到乙地经过的路程为x千米,则x的最大值是
A.11 B.8 C.7 D.5
2.已知点M(n,﹣n )在第二象限,过点M的直线y=kx+b(0<k<1)分别交x轴、y轴于点A,B,过点M作MN⊥x轴于点N,则下列点在线段AN的是( )
A.((k﹣1)n,0) B.((k+ )n,0))
C.( ,0) D.((k+1)n,0)
3.已知直线y=kx+b经过第一、二、四象限,那么直线y=bx+k一定不经过( )
A.第一象限; B.第二象限; C.第三象限; D.第四象限.
4.函数y=x的图象与函数y=2x+1的图象的交点坐标是( )
A.(1,1) B.(0,0)
C.( , ) D.(﹣ ,﹣ )
5.甲、乙两车从同地沿同一路线去600km外的某地取货,甲比乙先出发,他们去时所走的路程S(km)与时间t(h)之间的函数图象如图所示,则以下说法中正确的有( )
①甲比乙早出发8h;
②相遇前,乙的速度是甲的速度的5倍;
③相遇后甲提速了,乙降速了;
④乙出发2h后追上甲;
⑤甲比原计划(按初始速度行驶)晚到目的地4h.
A.2个 B.3个 C.4个 D.5个
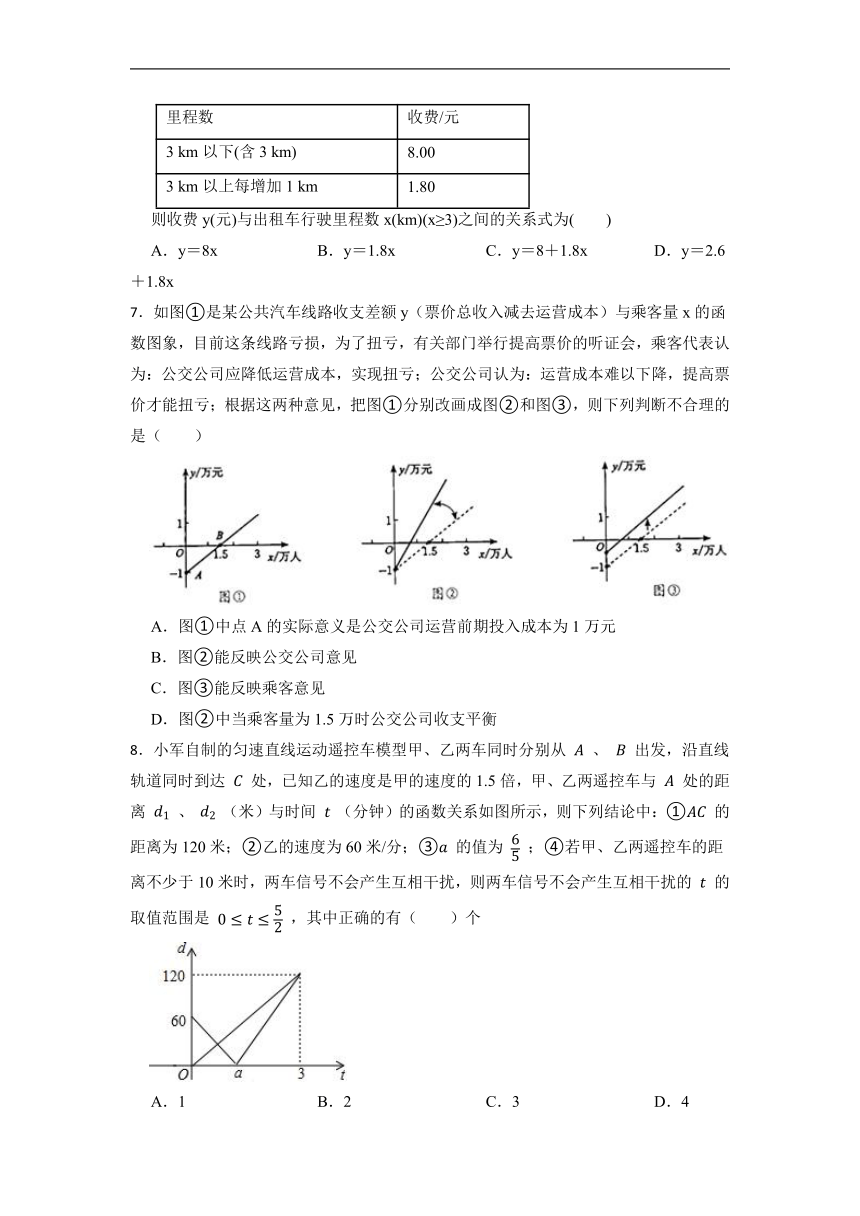
6.某校组织学生到距学校6 km的光明科技馆参观.王红准备乘出租车去科技馆,出租车的收费标准如下表:
里程数 收费/元
3 km以下(含3 km) 8.00
3 km以上每增加1 km 1.80
则收费y(元)与出租车行驶里程数x(km)(x≥3)之间的关系式为( )
A.y=8x B.y=1.8x C.y=8+1.8x D.y=2.6+1.8x
7.如图①是某公共汽车线路收支差额y(票价总收入减去运营成本)与乘客量x的函数图象,目前这条线路亏损,为了扭亏,有关部门举行提高票价的听证会,乘客代表认为:公交公司应降低运营成本,实现扭亏;公交公司认为:运营成本难以下降,提高票价才能扭亏;根据这两种意见,把图①分别改画成图②和图③,则下列判断不合理的是( )
A.图①中点A的实际意义是公交公司运营前期投入成本为1万元
B.图②能反映公交公司意见
C.图③能反映乘客意见
D.图②中当乘客量为1.5万时公交公司收支平衡
8.小军自制的匀速直线运动遥控车模型甲、乙两车同时分别从 、 出发,沿直线轨道同时到达 处,已知乙的速度是甲的速度的1.5倍,甲、乙两遥控车与 处的距离 、 (米)与时间 (分钟)的函数关系如图所示,则下列结论中:① 的距离为120米;②乙的速度为60米/分;③ 的值为 ;④若甲、乙两遥控车的距离不少于10米时,两车信号不会产生互相干扰,则两车信号不会产生互相干扰的 的取值范围是 ,其中正确的有( )个
A.1 B.2 C.3 D.4
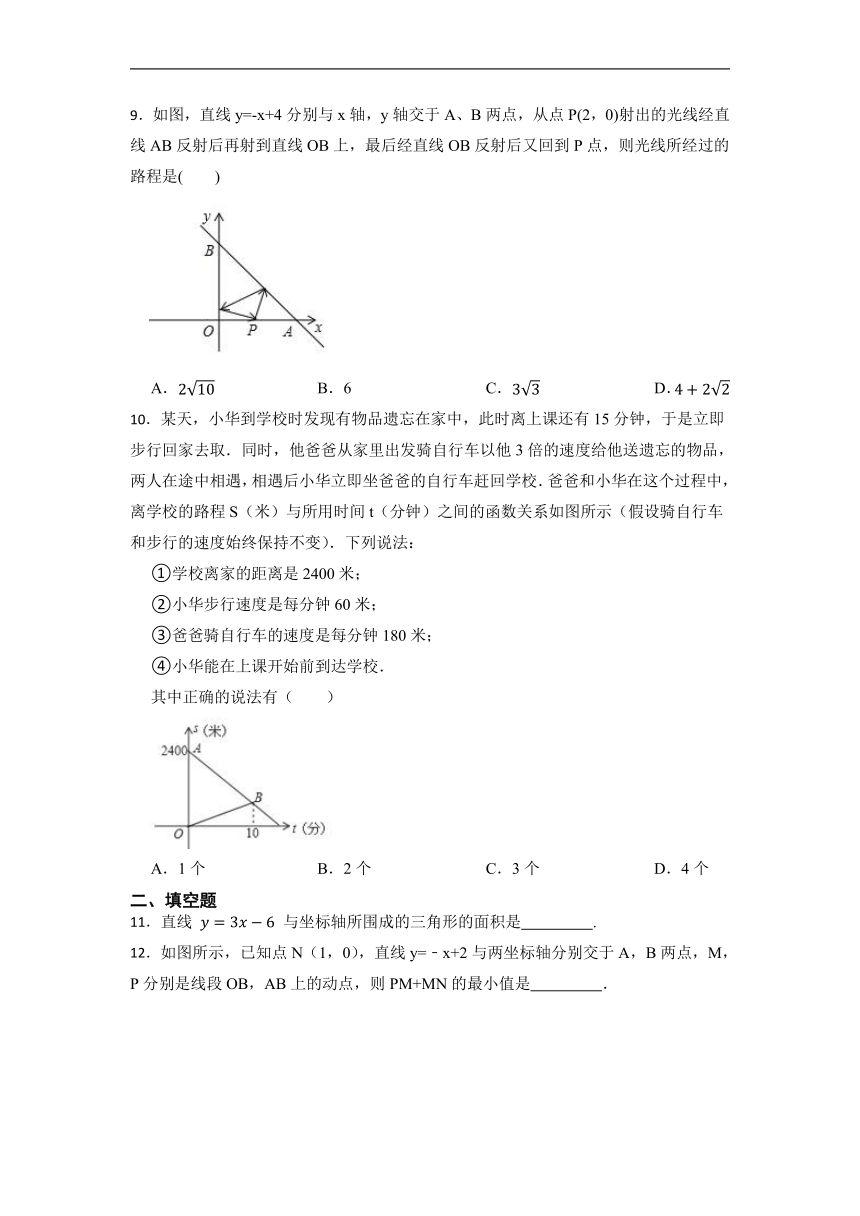
9.如图,直线y=-x+4分别与x轴,y轴交于A、B两点,从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( )
A. B.6 C. D.
10.某天,小华到学校时发现有物品遗忘在家中,此时离上课还有15分钟,于是立即步行回家去取.同时,他爸爸从家里出发骑自行车以他3倍的速度给他送遗忘的物品,两人在途中相遇,相遇后小华立即坐爸爸的自行车赶回学校.爸爸和小华在这个过程中,离学校的路程S(米)与所用时间t(分钟)之间的函数关系如图所示(假设骑自行车和步行的速度始终保持不变).下列说法:
①学校离家的距离是2400米;
②小华步行速度是每分钟60米;
③爸爸骑自行车的速度是每分钟180米;
④小华能在上课开始前到达学校.
其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.直线 与坐标轴所围成的三角形的面积是 .
12.如图所示,已知点N(1,0),直线y=﹣x+2与两坐标轴分别交于A,B两点,M,P分别是线段OB,AB上的动点,则PM+MN的最小值是 .
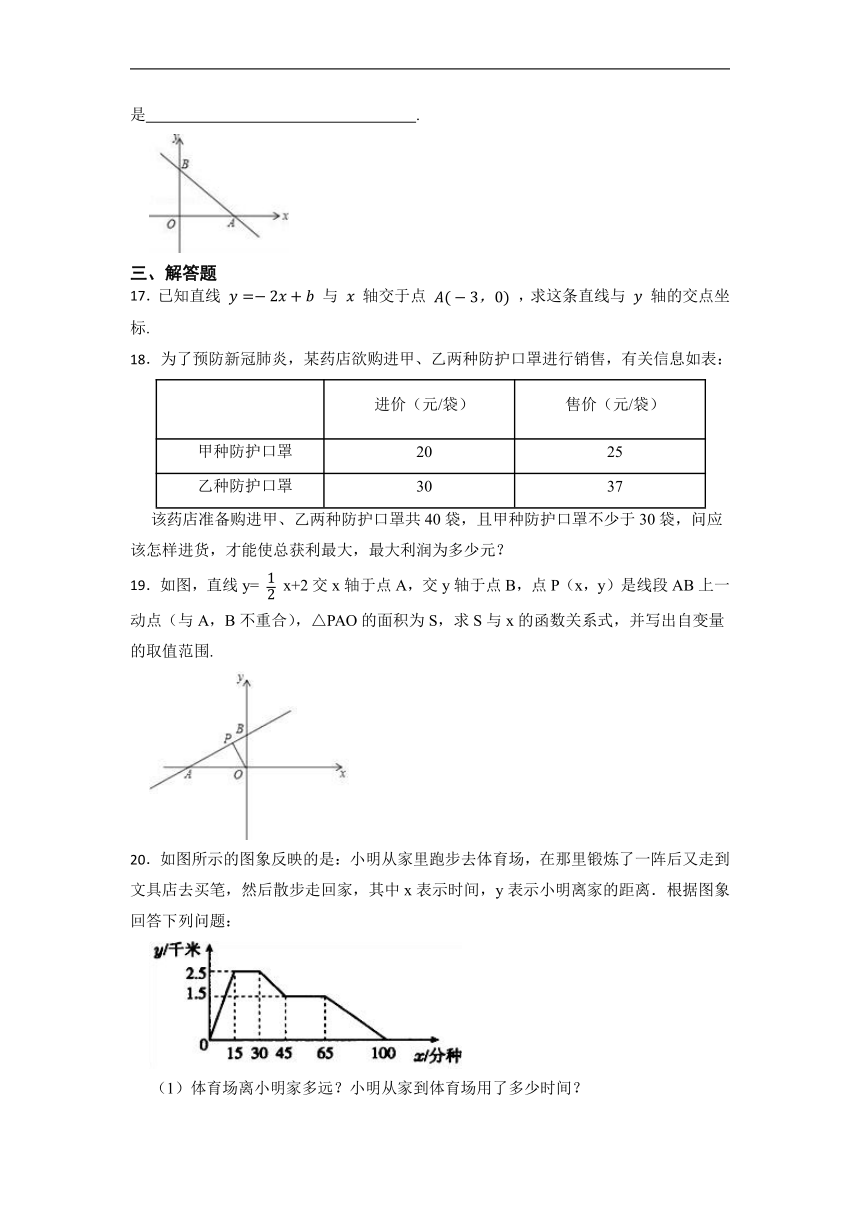
13.某市出租车公司规定:出租车收费与行驶路程关系如图所示.如果小明的姥姥乘出租车去小明家花了22元,那么小明的姥姥乘车路程有 千米.
14.一条笔直的公路上依次有A,B,C三地,甲,乙两人同时从A地出发,甲先使用共享单车,经过B地到达停车点C地后再步行返回B地,此时直接步行的乙也恰好到达B地.已知两人步行速度相同,两人离起点A的距离y(米)关于时间x(分)的函数关系如图,则 .
15.如图,在平面直角坐标系中,矩形AOBC的顶点A,B的坐标分别是A(0,4),B(4,0),作点A关于直线y=kx(k>0)的对称点P,△POB为等腰三角形,则点P的坐标为
16.如图,一次函数y=-x+1的图象与 轴、 轴分别交于点 ,点 在 轴上,要使 是以AB为腰的等腰三角形,那么点 的坐标是 .
三、解答题
17.已知直线 与 轴交于点 ,求这条直线与 轴的交点坐标.
18.为了预防新冠肺炎,某药店欲购进甲、乙两种防护口罩进行销售,有关信息如表:
进价(元/袋) 售价(元/袋)
甲种防护口罩 20 25
乙种防护口罩 30 37
该药店准备购进甲、乙两种防护口罩共40袋,且甲种防护口罩不少于30袋,问应该怎样进货,才能使总获利最大,最大利润为多少元?
19.如图,直线y= x+2交x轴于点A,交y轴于点B,点P(x,y)是线段AB上一动点(与A,B不重合),△PAO的面积为S,求S与x的函数关系式,并写出自变量的取值范围.
20.如图所示的图象反映的是:小明从家里跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家,其中x表示时间,y表示小明离家的距离.根据图象回答下列问题:
(1)体育场离小明家多远?小明从家到体育场用了多少时间?
(2)体育场离文具店多远?
(3)小明在文具店逗留了多少时间?
(4)小明从文具店回家的平均速度是多少?
21.如图1,长为60km的某段线路AB上有甲、乙两车,分别从南站A和北站B同时出发相向而行,到达B、A后立刻返回到出发站停止,速度均为30km/h,设甲车,乙车距南站A的路程分别为y甲,y乙(km)行驶时间为t(h).
(1)图2已画出y甲与t的函数图象,其中a= ,b= ,c= .
(2)分别写出0≤t≤2及2<t≤4时,y乙与时间t之间的函数关系式.
(3)在图2中补画y乙与t之间的函数图象,并观察图象得出在整个行驶过程中两车相遇的次数.
22.如图①所示,直线L:y=m(x+10)与x轴负半轴、y轴正半轴分别交于A、B两点.
(1)当OA=OB时,试确定直线L的解析式;
(2)在(1)的条件下,如图②所示,设Q为AB延长线上一点,作直线OQ,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=8,BN=6,求MN的长;
(3)当m取不同的值时,点B在y轴正半轴上运动,分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交y轴于P点,如图③.
问:当点B在y轴正半轴上运动时,试猜想PB的长是否为定值?若是,请求出其值;若不是,说明理由.
参考答案
1.B
2.D
3.B
4.C
5.B
6.D
7.D
8.C
9.A
10.D
11.6
12.
13.13
14.10
15.(,),(,﹣),(2,﹣2)或(2,2)
16. 或(-1,0).
17.解:将 代入 ,得:
,
解得: ,
∴一次函数的解析式为 .
当 时, ,
∴直线与 轴的交点坐标为(0,-6).
18.解:设购进甲种防护口罩x袋,则乙种防护口罩(40-x)袋,总利润为W元,根据题意得:
,
∵甲种防护口罩不少于30袋,
∴,
∵-2<0,
∴W随x的增大而减小,
∴当x=30时,W最大,最大值为元,
此时40-x=10,
答:购进甲种防护口罩30袋,乙种防护口罩10袋,才能使总获利最大,最大利润为220元.
19.解:∵令y= x+2=0,解得:x=-4,
∴点A的坐标为(-4,0),
∵令x=0,得y=2,
∴点B的坐标为(0,2),
∴OA=4,OB=2,
∵点P(x,y)是线段AB上一动点(与A,B不重合),
∴点P的坐标可表示为(x, x+2),
如图,作PC⊥AO于点C,
∵点P(x, x+2)在第二象限,
∴ x+2>0
∴PC= x+2
∴S= AO PC
= ×4×( x+2)
=x+4.
∴S与x的函数关系式为S=x+4(-4<x<0)
20.(1)解:体育场离小明家2.5千米,小明从家到体育场用了15分钟。
(2)解:体育场离文具店2.5-1.5=1(千米).
(3)解:小明在文具店逗留的时间为65-45=20(分钟).
(4)解:小明从文具店回家的平均速度是 = (千米/分钟).
21.解:(1)由题意,得
a=60,b=2,c=4.
故答案为:60,2,4;
(2)当0≤t≤2时,设y乙与时间t之间的函数关系式为y乙=kx+b,由题意,得
,
解得:
∴y乙=﹣30t+60
当2<t≤4时,设y乙与时间t之间的函数关系式为y乙=k1x+b1,由题意,得
,
解得:,
∴y乙=30t﹣60.
(3)列表为:
t 0 2 4
y乙=﹣30t+60(0≤t≤2) 60 0
y乙=30t﹣60(2<t≤4)
0 60
描点并连线为:
如图,由于两个图象有两个交点,所以在整个行驶过程中两车相遇次数为2.
22.解:(1)由题意知:A(﹣10,0),B(0,10m)
∵OA=OB,
∴10m=10,即m=1.
∴L的解析式y=x+10.
(2)∵AM⊥OQ,BN⊥OQ
∴∠AMO=∠BNO=90°
∴∠AOM+∠MAO=90°
∵∠AOM+BON=90°
∴∠MAO=∠NOB
在△AMO和△ONB中,
,
∴△AMO≌△ONB.
∴ON=AM,OM=BN.
∵AM=8,BN=6,
∴MN=AM+BN=14.
(3)PB的长为定值.
理由:如图所示:过点E作EG⊥y轴于G点.
∵△AEB为等腰直角三角形,
∴AB=EB,∠ABO+∠EBG=90°.
∵EG⊥BG,
∴∠GEB+∠EBG=90°.
∴∠ABO=∠GEB.
在△ABO和△EGB中,
,
∴△ABO≌△EGB.
∴BG=AO=10,OB=EG
∵△OBF为等腰直角三角形,
∴OB=BF
∴BF=EG.
在△BFP和△GEP中,
,
∴△BFP≌△GEP.
∴BP=GP=BG=5.
一、单选题
1.某种出租车收费标准是:起步价7元(即行驶距离不超过3千米需付7元车费),超过了3千米以后,每增加1千米加收2.4元(不足1千米按1千米计),某人乘这种出租车从甲地到乙地支付车费19元,设此人从甲地到乙地经过的路程为x千米,则x的最大值是
A.11 B.8 C.7 D.5
2.已知点M(n,﹣n )在第二象限,过点M的直线y=kx+b(0<k<1)分别交x轴、y轴于点A,B,过点M作MN⊥x轴于点N,则下列点在线段AN的是( )
A.((k﹣1)n,0) B.((k+ )n,0))
C.( ,0) D.((k+1)n,0)
3.已知直线y=kx+b经过第一、二、四象限,那么直线y=bx+k一定不经过( )
A.第一象限; B.第二象限; C.第三象限; D.第四象限.
4.函数y=x的图象与函数y=2x+1的图象的交点坐标是( )
A.(1,1) B.(0,0)
C.( , ) D.(﹣ ,﹣ )
5.甲、乙两车从同地沿同一路线去600km外的某地取货,甲比乙先出发,他们去时所走的路程S(km)与时间t(h)之间的函数图象如图所示,则以下说法中正确的有( )
①甲比乙早出发8h;
②相遇前,乙的速度是甲的速度的5倍;
③相遇后甲提速了,乙降速了;
④乙出发2h后追上甲;
⑤甲比原计划(按初始速度行驶)晚到目的地4h.
A.2个 B.3个 C.4个 D.5个
6.某校组织学生到距学校6 km的光明科技馆参观.王红准备乘出租车去科技馆,出租车的收费标准如下表:
里程数 收费/元
3 km以下(含3 km) 8.00
3 km以上每增加1 km 1.80
则收费y(元)与出租车行驶里程数x(km)(x≥3)之间的关系式为( )
A.y=8x B.y=1.8x C.y=8+1.8x D.y=2.6+1.8x
7.如图①是某公共汽车线路收支差额y(票价总收入减去运营成本)与乘客量x的函数图象,目前这条线路亏损,为了扭亏,有关部门举行提高票价的听证会,乘客代表认为:公交公司应降低运营成本,实现扭亏;公交公司认为:运营成本难以下降,提高票价才能扭亏;根据这两种意见,把图①分别改画成图②和图③,则下列判断不合理的是( )
A.图①中点A的实际意义是公交公司运营前期投入成本为1万元
B.图②能反映公交公司意见
C.图③能反映乘客意见
D.图②中当乘客量为1.5万时公交公司收支平衡
8.小军自制的匀速直线运动遥控车模型甲、乙两车同时分别从 、 出发,沿直线轨道同时到达 处,已知乙的速度是甲的速度的1.5倍,甲、乙两遥控车与 处的距离 、 (米)与时间 (分钟)的函数关系如图所示,则下列结论中:① 的距离为120米;②乙的速度为60米/分;③ 的值为 ;④若甲、乙两遥控车的距离不少于10米时,两车信号不会产生互相干扰,则两车信号不会产生互相干扰的 的取值范围是 ,其中正确的有( )个
A.1 B.2 C.3 D.4
9.如图,直线y=-x+4分别与x轴,y轴交于A、B两点,从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( )
A. B.6 C. D.
10.某天,小华到学校时发现有物品遗忘在家中,此时离上课还有15分钟,于是立即步行回家去取.同时,他爸爸从家里出发骑自行车以他3倍的速度给他送遗忘的物品,两人在途中相遇,相遇后小华立即坐爸爸的自行车赶回学校.爸爸和小华在这个过程中,离学校的路程S(米)与所用时间t(分钟)之间的函数关系如图所示(假设骑自行车和步行的速度始终保持不变).下列说法:
①学校离家的距离是2400米;
②小华步行速度是每分钟60米;
③爸爸骑自行车的速度是每分钟180米;
④小华能在上课开始前到达学校.
其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.直线 与坐标轴所围成的三角形的面积是 .
12.如图所示,已知点N(1,0),直线y=﹣x+2与两坐标轴分别交于A,B两点,M,P分别是线段OB,AB上的动点,则PM+MN的最小值是 .
13.某市出租车公司规定:出租车收费与行驶路程关系如图所示.如果小明的姥姥乘出租车去小明家花了22元,那么小明的姥姥乘车路程有 千米.
14.一条笔直的公路上依次有A,B,C三地,甲,乙两人同时从A地出发,甲先使用共享单车,经过B地到达停车点C地后再步行返回B地,此时直接步行的乙也恰好到达B地.已知两人步行速度相同,两人离起点A的距离y(米)关于时间x(分)的函数关系如图,则 .
15.如图,在平面直角坐标系中,矩形AOBC的顶点A,B的坐标分别是A(0,4),B(4,0),作点A关于直线y=kx(k>0)的对称点P,△POB为等腰三角形,则点P的坐标为
16.如图,一次函数y=-x+1的图象与 轴、 轴分别交于点 ,点 在 轴上,要使 是以AB为腰的等腰三角形,那么点 的坐标是 .
三、解答题
17.已知直线 与 轴交于点 ,求这条直线与 轴的交点坐标.
18.为了预防新冠肺炎,某药店欲购进甲、乙两种防护口罩进行销售,有关信息如表:
进价(元/袋) 售价(元/袋)
甲种防护口罩 20 25
乙种防护口罩 30 37
该药店准备购进甲、乙两种防护口罩共40袋,且甲种防护口罩不少于30袋,问应该怎样进货,才能使总获利最大,最大利润为多少元?
19.如图,直线y= x+2交x轴于点A,交y轴于点B,点P(x,y)是线段AB上一动点(与A,B不重合),△PAO的面积为S,求S与x的函数关系式,并写出自变量的取值范围.
20.如图所示的图象反映的是:小明从家里跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家,其中x表示时间,y表示小明离家的距离.根据图象回答下列问题:
(1)体育场离小明家多远?小明从家到体育场用了多少时间?
(2)体育场离文具店多远?
(3)小明在文具店逗留了多少时间?
(4)小明从文具店回家的平均速度是多少?
21.如图1,长为60km的某段线路AB上有甲、乙两车,分别从南站A和北站B同时出发相向而行,到达B、A后立刻返回到出发站停止,速度均为30km/h,设甲车,乙车距南站A的路程分别为y甲,y乙(km)行驶时间为t(h).
(1)图2已画出y甲与t的函数图象,其中a= ,b= ,c= .
(2)分别写出0≤t≤2及2<t≤4时,y乙与时间t之间的函数关系式.
(3)在图2中补画y乙与t之间的函数图象,并观察图象得出在整个行驶过程中两车相遇的次数.
22.如图①所示,直线L:y=m(x+10)与x轴负半轴、y轴正半轴分别交于A、B两点.
(1)当OA=OB时,试确定直线L的解析式;
(2)在(1)的条件下,如图②所示,设Q为AB延长线上一点,作直线OQ,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=8,BN=6,求MN的长;
(3)当m取不同的值时,点B在y轴正半轴上运动,分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交y轴于P点,如图③.
问:当点B在y轴正半轴上运动时,试猜想PB的长是否为定值?若是,请求出其值;若不是,说明理由.
参考答案
1.B
2.D
3.B
4.C
5.B
6.D
7.D
8.C
9.A
10.D
11.6
12.
13.13
14.10
15.(,),(,﹣),(2,﹣2)或(2,2)
16. 或(-1,0).
17.解:将 代入 ,得:
,
解得: ,
∴一次函数的解析式为 .
当 时, ,
∴直线与 轴的交点坐标为(0,-6).
18.解:设购进甲种防护口罩x袋,则乙种防护口罩(40-x)袋,总利润为W元,根据题意得:
,
∵甲种防护口罩不少于30袋,
∴,
∵-2<0,
∴W随x的增大而减小,
∴当x=30时,W最大,最大值为元,
此时40-x=10,
答:购进甲种防护口罩30袋,乙种防护口罩10袋,才能使总获利最大,最大利润为220元.
19.解:∵令y= x+2=0,解得:x=-4,
∴点A的坐标为(-4,0),
∵令x=0,得y=2,
∴点B的坐标为(0,2),
∴OA=4,OB=2,
∵点P(x,y)是线段AB上一动点(与A,B不重合),
∴点P的坐标可表示为(x, x+2),
如图,作PC⊥AO于点C,
∵点P(x, x+2)在第二象限,
∴ x+2>0
∴PC= x+2
∴S= AO PC
= ×4×( x+2)
=x+4.
∴S与x的函数关系式为S=x+4(-4<x<0)
20.(1)解:体育场离小明家2.5千米,小明从家到体育场用了15分钟。
(2)解:体育场离文具店2.5-1.5=1(千米).
(3)解:小明在文具店逗留的时间为65-45=20(分钟).
(4)解:小明从文具店回家的平均速度是 = (千米/分钟).
21.解:(1)由题意,得
a=60,b=2,c=4.
故答案为:60,2,4;
(2)当0≤t≤2时,设y乙与时间t之间的函数关系式为y乙=kx+b,由题意,得
,
解得:
∴y乙=﹣30t+60
当2<t≤4时,设y乙与时间t之间的函数关系式为y乙=k1x+b1,由题意,得
,
解得:,
∴y乙=30t﹣60.
(3)列表为:
t 0 2 4
y乙=﹣30t+60(0≤t≤2) 60 0
y乙=30t﹣60(2<t≤4)
0 60
描点并连线为:
如图,由于两个图象有两个交点,所以在整个行驶过程中两车相遇次数为2.
22.解:(1)由题意知:A(﹣10,0),B(0,10m)
∵OA=OB,
∴10m=10,即m=1.
∴L的解析式y=x+10.
(2)∵AM⊥OQ,BN⊥OQ
∴∠AMO=∠BNO=90°
∴∠AOM+∠MAO=90°
∵∠AOM+BON=90°
∴∠MAO=∠NOB
在△AMO和△ONB中,
,
∴△AMO≌△ONB.
∴ON=AM,OM=BN.
∵AM=8,BN=6,
∴MN=AM+BN=14.
(3)PB的长为定值.
理由:如图所示:过点E作EG⊥y轴于G点.
∵△AEB为等腰直角三角形,
∴AB=EB,∠ABO+∠EBG=90°.
∵EG⊥BG,
∴∠GEB+∠EBG=90°.
∴∠ABO=∠GEB.
在△ABO和△EGB中,
,
∴△ABO≌△EGB.
∴BG=AO=10,OB=EG
∵△OBF为等腰直角三角形,
∴OB=BF
∴BF=EG.
在△BFP和△GEP中,
,
∴△BFP≌△GEP.
∴BP=GP=BG=5.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
