2022-2023学年华东师大版八年级数学上册第12章整式的乘除 解答专题达标测评(word、含答案)
文档属性
| 名称 | 2022-2023学年华东师大版八年级数学上册第12章整式的乘除 解答专题达标测评(word、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 100.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 21:33:22 | ||
图片预览



文档简介
2022-2023学年华东师大版八年级数学上册《第12章整式的乘除》
解答专题达标测评(附答案)
(共20小题,每小题6分,满分120分)
1.计算:
(1)(x3 x2)3;
(2)(3m﹣n)(﹣n﹣3m).
2.将下列各式分解因式:
(1)x2+2x﹣15;
(2)9(x+2y)2﹣4(x﹣y)2.
3.化简:.
4.计算:(9x﹣2y)(x+y)﹣(﹣3x+y)(﹣3x﹣y).
5.因式分解:
(1)9x2﹣6xy+y2.
(2)(x+1)(x﹣3)+4.
6.计算:(a2)3﹣a2×a4+(2a4)2÷a2.
7.化简:a2 (﹣a)4﹣(3a3)2+(﹣2a2)3.
8.已知5a=3,5b=8,5c=72.
(1)求(5a)2的值.
(2)求5a﹣b+c的值.
(3)直接写出字母a、b、c之间的数量关系为 .
9.计算:
(1)a3 a (﹣a)
(2)(y2)3÷y6 y
(3)8×4n÷2n﹣1
(4)
10.因式分解:
(1)(x+3y)2﹣x﹣3y;
(2)(a2+4)2﹣16a2.
11.因式分解:
(1)ax2﹣4ax+4a;
(2)x2(m﹣n)+y2(n﹣m);
(3)(x+2)(x+4)﹣3;
(4)9(a+b)2﹣(a﹣b)2.
12.已知m﹣n=4,mn=﹣3.
(1)计算:m2+n2;
(2)求(m2﹣4)(n2﹣4)的值;
(3)求8m 32n÷4m+2n的值.
13.根据已知条件,求出下列代数式的值:
(1)已知x+2y=4,xy=1,求代数式x2+4y2+3xy的值;
(2)已知m2+m﹣1=0,求代数式m3+2m2+2022的值.
14.如图,边长为a的正方形中有一个边长为b(b<a)的小正方形,如图2是由图1中的阴影部分拼成的一个长方形.
(1)设图1阴影部分的面积为S1,图2中阴影部分的面积为S2,请直接用含a,b的式子表示S1= ,S2= ,写出上述过程中所揭示的乘法公式 ;
(2)直接应用,利用这个公式计算:
①(﹣x﹣y)(y﹣x);
②102×98.
(3)拓展应用,试利用这个公式求下面代数式的结果.
(3+1)×(32+1)×(34+1)×(38+1)×(316+1)×…×(31024+1)+1.
15.(1)请用两种不同的方法表示图中阴影部分的面积和.
方法1: ;
方法2: .
(2)请你直接写出三个代数式:(a+b)2,a2+b2,ab之间的等量关系.
(3)根据(2)中的等量关系,解决如下问题:
①已知m+n=5,m2+n2=20,求mn和(m﹣n)2的值;
②已知(x﹣2021)2+(x﹣2023)2=74,求(x﹣2022)2的值.
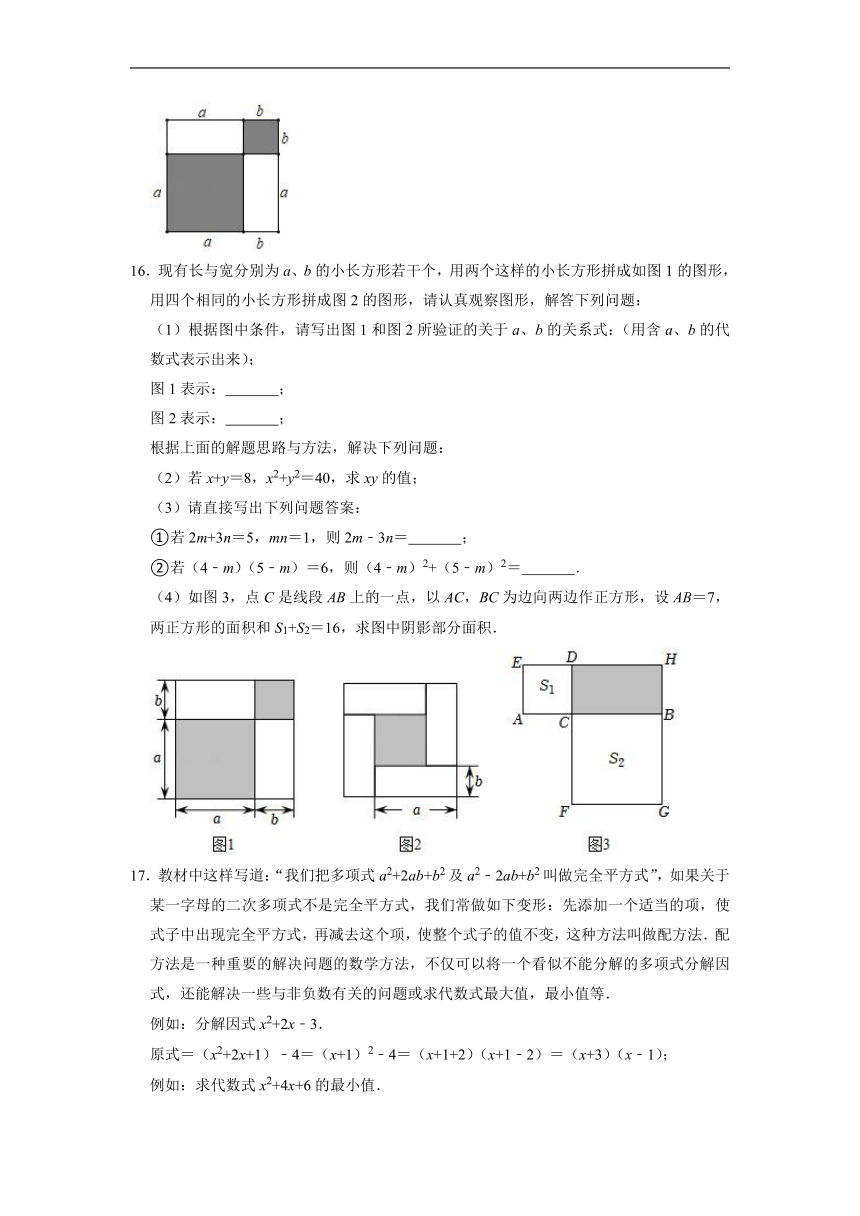
16.现有长与宽分别为a、b的小长方形若干个,用两个这样的小长方形拼成如图1的图形,用四个相同的小长方形拼成图2的图形,请认真观察图形,解答下列问题:
(1)根据图中条件,请写出图1和图2所验证的关于a、b的关系式:(用含a、b的代数式表示出来);
图1表示: ;
图2表示: ;
根据上面的解题思路与方法,解决下列问题:
(2)若x+y=8,x2+y2=40,求xy的值;
(3)请直接写出下列问题答案:
①若2m+3n=5,mn=1,则2m﹣3n= ;
②若(4﹣m)(5﹣m)=6,则(4﹣m)2+(5﹣m)2= .
(4)如图3,点C是线段AB上的一点,以AC,BC为边向两边作正方形,设AB=7,两正方形的面积和S1+S2=16,求图中阴影部分面积.
17.教材中这样写道:“我们把多项式a2+2ab+b2及a2﹣2ab+b2叫做完全平方式”,如果关于某一字母的二次多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等.
例如:分解因式x2+2x﹣3.
原式=(x2+2x+1)﹣4=(x+1)2﹣4=(x+1+2)(x+1﹣2)=(x+3)(x﹣1);
例如:求代数式x2+4x+6的最小值.
原式=x2+4x+4+2=(x+2)2+2.
∵(x+2)2≥0,
∴当x=﹣2时,x2+4x+6有最小值是2.
根据阅读材料用配方法解决下列问题:
(1)分解因式:m2﹣4m﹣5= ;
(2)求代数式x2﹣6x+12的最小值;
(3)若y=﹣x2+2x﹣3,当x= 时,y有最 值(填“大”或“小”),这个值是 ;
(4)当a,b,c分别为△ABC的三边时,且满足a2+b2+c2﹣6a﹣10b﹣8c+50=0时,判断△ABC的形状并说明理由.
18.乘法公式的探究及应用:
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b、宽为a的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法表示图2大正方形的面积.
方法1: ;方法2: ;
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的数量关系: ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=21,求ab的值;
②已知(2022﹣a)2+(a﹣2020)2=10,求(2022﹣a)(a﹣2020)的值.
19.数学活动课上,刘老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
由图2,可得出三个代数式:(a+b)2,a2+b2,ab之间的等量关系;
(1)根据上述方法,要拼出一个面积为(a+2b)(a+b)的矩形,需要A卡片1张,B卡片2张,C卡片 张.
(2)根据得出的等量关系,解决如下问题:
①已知:a+b=6,a2+b2=14,求ab的值;
②已知(x﹣2020)2+(x﹣2022)2=10,求(x﹣2021)2的值.
20.如图,某中学校园内有一块长为(3a+2b)米,宽为(2a+b)米的长方形地块,学校计划在中间留一块长为(2a﹣b)米,宽为2b米的小长方形地块修建一座雕像,然后将阴影部分进行绿化.
(1)求长方形地块的面积;(用含a,b的代数式表示)
(2)求雕像的面积;(用含a,b的代数式表示)
(3)当a=100,b=40时,求绿化部分的面积.
参考答案
1.解:(1)(x3 x2)3
=(x5)3
=x15;
(2)(3m﹣n)(﹣n﹣3m)
=(﹣n)2﹣(3m)2
=n2﹣9m2.
2.解:(1)原式=(x﹣3)(x+5);
(2)原式=[3(x+2y)+2(x﹣y)][3(x+2y)﹣2(x﹣y)]
=(5x+4y)(x+8y).
3.解:原式=4x﹣4x
=2xy﹣.
4.解:(9x﹣2y)(x+y)﹣(﹣3x+y)(﹣3x﹣y)
=9x2+9xy﹣2xy﹣2y2﹣(9x2﹣y2)
=9x2+9xy﹣2xy﹣2y2﹣9x2+y2
=7xy﹣y2.
5.解:(1)9x2﹣6xy+y2
=(3x)2﹣6xy+y2
=(3x﹣y)2;
(2)(x+1)(x﹣3)+4
=x2﹣2x+1
=(x﹣1)2.
6.解:原式=a6﹣a6+4a8÷a2
=a6﹣a6+4a6
=4a6.
7.解:a2 (﹣a)4﹣(3a3)2+(﹣2a2)3.
=a2 a4﹣9a6﹣8a6
=a6﹣9a6﹣8a6
=﹣16a6.
8.解:(1)∵5a=3,
∴(5a)2=32=9;
(2)∵5a=3,5b=8,5c=72,
∴5a﹣b+c===27;
(3)c=2a+b;
故答案为:c=2a+b.
9.解:(1)a3 a (﹣a)=﹣a3+1+1=﹣a5;
(2)(y2)3÷y6 y=y6÷y6 y=1 y=y;
(3)8×4n÷2n﹣1=23×22n÷2n﹣1=22n+3÷2n﹣1=22n+3﹣n+1=2n+4;
(4)
=﹣1+﹣+1
=﹣1+1+()
=0+
=.
10.解:(1)原式=(x+3y)2﹣(x+3y)
=(x+3y)(x+3y﹣1);
(2)原式=(a2+4)2﹣(4a)2
=(a2+4+4a)(a2+4﹣4a)
=(a+2)2(a﹣2)2.
11.解:(1)原式=a(x2﹣4x+4)
=a(x﹣2)2;
(2)原式=x2(m﹣n)﹣y2(m﹣n)
=(m﹣n)(x2﹣y2)
=(m﹣n)(x+y)(x﹣y);
(3)原式=x2+6x+8﹣3
=x2+6x+5
=(x+1)(x+5);
(4)原式=[3(a+b)+(a﹣b)][3(a+b)﹣(a﹣b]
=(4a+2b)(2a+4b)
=4(2a+b)(a+2b).
12.解:(1)∵m﹣n=4,mn=﹣3,
∴m2+n2
=(m﹣n)2+2mn
=42+2×(﹣3)
=16﹣6
=10;
(2)(m2﹣4)(n2﹣4)
=(mn)2﹣4(m2+n2)+16,
当mn=﹣3,m2+n2=10时,
原式=(﹣3)2﹣4×10+16
=9﹣40+16
=﹣15;
(3)8m 32n÷4m+2n
=(23)m (25)n÷(22)m+2n
=23m 25n÷22m+4n
=23m+5n÷22m+4n
=23m+5n﹣2m﹣4n
=2m+n,
∵m﹣n=4,mn=﹣3
∴(m+n)2
=(m﹣n)2+4mn
=42+4×(﹣3)
=16﹣12
=4,
∴m+n=2或﹣2,
∴2m+n
=22或2﹣2
=4或.
13.解:(1)x2+4y2+3xy
=x2+4y2+4xy﹣xy
=(x+2y)2﹣xy
∵x+2y=4,xy=1,
∴原式=42﹣1
=15.
(2)m3+2m2+2022
=m(m2+m)+m2+2022
∵m2+m﹣1=0,
∴m2+m=1
原式=m+m2+2022
=1+2022
=2023
14.解:(1)S1=a2﹣b2,S2=(a+b)(a﹣b),
∵S1=S2,
∴a2﹣b2=(a+b)(a﹣b).
(2)①(﹣x﹣y)(y﹣x)=(﹣x)2﹣y2=x2﹣y2;
②102×98=(100+2)×(100﹣2)=9996.
(3)(3+1)×(32+1)×(34+1)×(38+1)×(316+1)......×(31024+1)+1,
=(3﹣1)×[(3+1)×(32+1)×(34+1)×(38+1)×(316+1)......×(31024+1)]÷(3﹣1)+1,
=(32﹣1)×(32+1)×(34+1)×(38+1)×(316+1)......×(31024+1)÷2+1,
=[(31024)2﹣12]÷2+1,
=(32048﹣1)÷2+1,
=.
15.解:(1)方法1:两个阴影部分的面积和就是边长为a的正方形,与边长为b的正方形的面积和,即a2+b2;
方法2:两个阴影部分的面积和也可以看作从边长为a+b的正方形面积中减去两个长为a,宽为b的长方形面积,即(a+b)2﹣2ab;
故答案为:a2+b2,(a+b)2﹣2ab;
(2)由(1)得,a2+b2=(a+b)2﹣2ab;
(3)①∵m+n=5,
∴(m+n)2=25=m2+2mn+n2,
∵m2+n2=20,
∴2mn=5,
即mn=;
(m﹣n)2=m2﹣2mn+n2=20﹣5=15,
答:mn=,(m﹣n)2=15;
②设a=x﹣2021,b=x﹣2023,则a﹣b=2,a2+b2=(x﹣2021)2+(x﹣2023)2=74,
所以ab===35,
即(x﹣2021)(x﹣2023)=35,
所以[(x﹣2022)+1][(x﹣2022)﹣1]=(x﹣2022)2﹣1=35,
即(x﹣2022)2=36.
16.解:(1)图1中,由图可知S大正方形=(a+b)2,
S组成大正方形的四部分的面积之和=a2+b2+2ab,
由题意得,S大正方形=S组成大正方形的四部分的面积之和,
即(a+b)2=a2+b2+2ab,
故答案为:(a+b)2=a2+b2+2ab.
图2中,由图可知S大正方形=(a+b)2,S小正方形=(a﹣b)2,S四个长方形=4ab,
由题图可知,S大正方形=S小正方形+S四个长方形,
即(a+b)2=(a﹣b)2+4ab,
故答案为:(a+b)2=(a﹣b)2+4ab.
(2)∵(x+y)2=x2+y2+2xy,
∴xy=【(x+y)2﹣(x2+y2)】
∵x+y=8,x2+y2=40,
∴xy=(64﹣40)
=12.
(3)①由图2可得(2m﹣3n)2=(2m+3n)2﹣24mn,
∵2m+3n=5,mn=1,
∴(2m﹣3n)2=52﹣24=1,
∴2m﹣3n=±1.
故答案为:±1.
②由图1可得【(4﹣m)﹣(5﹣m)】2=(4﹣m)2+(5﹣m)2﹣2(4﹣m)(5﹣m),
∴(4﹣m)2+(5﹣m)2=【(4﹣m)﹣(5﹣m)】2+2(4﹣m)(5﹣m),
∵(4﹣m)(5﹣m)=6,
∴原式=1+2×6=13.
故答案为:13.
(4)由题意得AB=AC+CB,
∵AB=7,
∴AC+CB=7,
∵S1+S2=16,
∴AC2+CB2=16,
∵(AC+BC)2=AC2+CB2+2AC CB,
∴AC CB=[(AC+CB)2﹣(AC2+CB2)]
=(49﹣16)
=,
∴S阴影=CD CB=AC CB=.
即图中阴影部分的面积为.
17.解:(1)m2﹣4m﹣5=m2﹣4m+4﹣4﹣5=(m﹣2)2﹣9=(m﹣2+3)(m﹣2﹣3)=(m+1)(m﹣5).
故答案为:(m+1)(m﹣5).
(2)x2﹣6x+12=x2﹣6x+9+3=(x﹣3)2+3;
∴x2﹣6x+12的最小值是3.
故答案为;3.
(3)y=﹣x2+2x﹣3,
y=﹣x2+2x﹣1﹣2,
y=﹣(x+1)2﹣2,
∴当x=﹣1的时候,y有最大值﹣2.
故答案为:若y=﹣x2+2x﹣3,当x=﹣1时,y有最大值,这个值是﹣2.
(4 a2+b2+c2﹣6a﹣10b﹣8c+50=0,
a2﹣6a+9+b2﹣10b+25+c2﹣8c+16=0,
(a﹣3)2+(b﹣5)2+(c﹣4)2=0,
三个完全平方式子的和为0,所以三个完全平方式子分别等于0.
a﹣3=0,b﹣5=0,c﹣4=0,
得,a=3,b=5,c=4.
∴△ABC是直角三角形.
故答案为:△ABC是直角三角形.
18.解:(1)方法1:大正方形的边长为(a+b),
∴S=(a+b)2;
方法2:大正方形=各个部分相加之和,
∴S=a2+2ab+b2.
故答案为:(a+b)2,a2+2ab+b2.
(2)由图2可得总面积减掉两个小矩形面积等于两个正方形面积之和,
即(a+b)2﹣2ab=a2+b2.
故答案为:(a+b)2=a2+b2+2ab.
(3)①∵a+b=5,
∴(a+b)2=25,
a2+b2=21,
∴2ab=(a+b)2﹣(a2+b2)=25﹣21=4,
∴ab=2.
②设m=2022﹣a,n=a﹣2020,
则m+n=2,m2+n2=(2022﹣a)2+(a﹣2020)2=10,
由(m+n)2=m2+n2+2mn得,
4=10+2mn,
∴mn=﹣3,
(2022﹣a)(a﹣2020)=mn=﹣3,
即(2022﹣a)(a﹣2020)的值为﹣3.
19.解:(1)若要拼出一个面积为(a+2b)(a+b)的矩形,则需要A号卡片1张,B号卡片2张,C号卡片3张.
故答案为:3.
(2)①∵(a+b)2=a2+b2+2ab,
∴2ab+14=36,
∴ab=11;
②(x﹣2020)2+(x﹣2022)2=10,
∵[(x﹣2020)﹣(x﹣2022)]2=(x﹣2020)2+(x﹣2022)2﹣2(x﹣2020)(x﹣2022),
∴4=10﹣2(x﹣2020)(x﹣2022),
∴2(x﹣2020)(x﹣2022)=6,
∵[(x﹣2020)+(x﹣2022)]2=(x﹣2020)2+(x﹣2022)2+2(x﹣2020)(x﹣2022),
∴[2(x﹣2021)]2=10+6=16,即4(x﹣2021)2=16,
∴(x﹣2021)2=4.
20.解:(1)∵(3a+2b)×(2a+b)=(6a2+7ab+2b2)平方米,
∴长方形地块的面积为(6a2+7ab+2b2)平方米;
(2)∵(2a﹣b)×2b=(4ab﹣2b2)平方米,
∴雕像的面积为(4ab﹣2b2)平方米;
(3)∵绿化部分的面积为6a2+7ab+2b2﹣(4ab﹣2b2)=(6a2+3ab+4b2)平方米;
∴当a=100,b=40时,
6a2+3ab+4b2
=6×100×100+3×100×40+4×40×40
=78400(平方米),
∴绿化部分的面积为78400平方米.
解答专题达标测评(附答案)
(共20小题,每小题6分,满分120分)
1.计算:
(1)(x3 x2)3;
(2)(3m﹣n)(﹣n﹣3m).
2.将下列各式分解因式:
(1)x2+2x﹣15;
(2)9(x+2y)2﹣4(x﹣y)2.
3.化简:.
4.计算:(9x﹣2y)(x+y)﹣(﹣3x+y)(﹣3x﹣y).
5.因式分解:
(1)9x2﹣6xy+y2.
(2)(x+1)(x﹣3)+4.
6.计算:(a2)3﹣a2×a4+(2a4)2÷a2.
7.化简:a2 (﹣a)4﹣(3a3)2+(﹣2a2)3.
8.已知5a=3,5b=8,5c=72.
(1)求(5a)2的值.
(2)求5a﹣b+c的值.
(3)直接写出字母a、b、c之间的数量关系为 .
9.计算:
(1)a3 a (﹣a)
(2)(y2)3÷y6 y
(3)8×4n÷2n﹣1
(4)
10.因式分解:
(1)(x+3y)2﹣x﹣3y;
(2)(a2+4)2﹣16a2.
11.因式分解:
(1)ax2﹣4ax+4a;
(2)x2(m﹣n)+y2(n﹣m);
(3)(x+2)(x+4)﹣3;
(4)9(a+b)2﹣(a﹣b)2.
12.已知m﹣n=4,mn=﹣3.
(1)计算:m2+n2;
(2)求(m2﹣4)(n2﹣4)的值;
(3)求8m 32n÷4m+2n的值.
13.根据已知条件,求出下列代数式的值:
(1)已知x+2y=4,xy=1,求代数式x2+4y2+3xy的值;
(2)已知m2+m﹣1=0,求代数式m3+2m2+2022的值.
14.如图,边长为a的正方形中有一个边长为b(b<a)的小正方形,如图2是由图1中的阴影部分拼成的一个长方形.
(1)设图1阴影部分的面积为S1,图2中阴影部分的面积为S2,请直接用含a,b的式子表示S1= ,S2= ,写出上述过程中所揭示的乘法公式 ;
(2)直接应用,利用这个公式计算:
①(﹣x﹣y)(y﹣x);
②102×98.
(3)拓展应用,试利用这个公式求下面代数式的结果.
(3+1)×(32+1)×(34+1)×(38+1)×(316+1)×…×(31024+1)+1.
15.(1)请用两种不同的方法表示图中阴影部分的面积和.
方法1: ;
方法2: .
(2)请你直接写出三个代数式:(a+b)2,a2+b2,ab之间的等量关系.
(3)根据(2)中的等量关系,解决如下问题:
①已知m+n=5,m2+n2=20,求mn和(m﹣n)2的值;
②已知(x﹣2021)2+(x﹣2023)2=74,求(x﹣2022)2的值.
16.现有长与宽分别为a、b的小长方形若干个,用两个这样的小长方形拼成如图1的图形,用四个相同的小长方形拼成图2的图形,请认真观察图形,解答下列问题:
(1)根据图中条件,请写出图1和图2所验证的关于a、b的关系式:(用含a、b的代数式表示出来);
图1表示: ;
图2表示: ;
根据上面的解题思路与方法,解决下列问题:
(2)若x+y=8,x2+y2=40,求xy的值;
(3)请直接写出下列问题答案:
①若2m+3n=5,mn=1,则2m﹣3n= ;
②若(4﹣m)(5﹣m)=6,则(4﹣m)2+(5﹣m)2= .
(4)如图3,点C是线段AB上的一点,以AC,BC为边向两边作正方形,设AB=7,两正方形的面积和S1+S2=16,求图中阴影部分面积.
17.教材中这样写道:“我们把多项式a2+2ab+b2及a2﹣2ab+b2叫做完全平方式”,如果关于某一字母的二次多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等.
例如:分解因式x2+2x﹣3.
原式=(x2+2x+1)﹣4=(x+1)2﹣4=(x+1+2)(x+1﹣2)=(x+3)(x﹣1);
例如:求代数式x2+4x+6的最小值.
原式=x2+4x+4+2=(x+2)2+2.
∵(x+2)2≥0,
∴当x=﹣2时,x2+4x+6有最小值是2.
根据阅读材料用配方法解决下列问题:
(1)分解因式:m2﹣4m﹣5= ;
(2)求代数式x2﹣6x+12的最小值;
(3)若y=﹣x2+2x﹣3,当x= 时,y有最 值(填“大”或“小”),这个值是 ;
(4)当a,b,c分别为△ABC的三边时,且满足a2+b2+c2﹣6a﹣10b﹣8c+50=0时,判断△ABC的形状并说明理由.
18.乘法公式的探究及应用:
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b、宽为a的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法表示图2大正方形的面积.
方法1: ;方法2: ;
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的数量关系: ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=21,求ab的值;
②已知(2022﹣a)2+(a﹣2020)2=10,求(2022﹣a)(a﹣2020)的值.
19.数学活动课上,刘老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
由图2,可得出三个代数式:(a+b)2,a2+b2,ab之间的等量关系;
(1)根据上述方法,要拼出一个面积为(a+2b)(a+b)的矩形,需要A卡片1张,B卡片2张,C卡片 张.
(2)根据得出的等量关系,解决如下问题:
①已知:a+b=6,a2+b2=14,求ab的值;
②已知(x﹣2020)2+(x﹣2022)2=10,求(x﹣2021)2的值.
20.如图,某中学校园内有一块长为(3a+2b)米,宽为(2a+b)米的长方形地块,学校计划在中间留一块长为(2a﹣b)米,宽为2b米的小长方形地块修建一座雕像,然后将阴影部分进行绿化.
(1)求长方形地块的面积;(用含a,b的代数式表示)
(2)求雕像的面积;(用含a,b的代数式表示)
(3)当a=100,b=40时,求绿化部分的面积.
参考答案
1.解:(1)(x3 x2)3
=(x5)3
=x15;
(2)(3m﹣n)(﹣n﹣3m)
=(﹣n)2﹣(3m)2
=n2﹣9m2.
2.解:(1)原式=(x﹣3)(x+5);
(2)原式=[3(x+2y)+2(x﹣y)][3(x+2y)﹣2(x﹣y)]
=(5x+4y)(x+8y).
3.解:原式=4x﹣4x
=2xy﹣.
4.解:(9x﹣2y)(x+y)﹣(﹣3x+y)(﹣3x﹣y)
=9x2+9xy﹣2xy﹣2y2﹣(9x2﹣y2)
=9x2+9xy﹣2xy﹣2y2﹣9x2+y2
=7xy﹣y2.
5.解:(1)9x2﹣6xy+y2
=(3x)2﹣6xy+y2
=(3x﹣y)2;
(2)(x+1)(x﹣3)+4
=x2﹣2x+1
=(x﹣1)2.
6.解:原式=a6﹣a6+4a8÷a2
=a6﹣a6+4a6
=4a6.
7.解:a2 (﹣a)4﹣(3a3)2+(﹣2a2)3.
=a2 a4﹣9a6﹣8a6
=a6﹣9a6﹣8a6
=﹣16a6.
8.解:(1)∵5a=3,
∴(5a)2=32=9;
(2)∵5a=3,5b=8,5c=72,
∴5a﹣b+c===27;
(3)c=2a+b;
故答案为:c=2a+b.
9.解:(1)a3 a (﹣a)=﹣a3+1+1=﹣a5;
(2)(y2)3÷y6 y=y6÷y6 y=1 y=y;
(3)8×4n÷2n﹣1=23×22n÷2n﹣1=22n+3÷2n﹣1=22n+3﹣n+1=2n+4;
(4)
=﹣1+﹣+1
=﹣1+1+()
=0+
=.
10.解:(1)原式=(x+3y)2﹣(x+3y)
=(x+3y)(x+3y﹣1);
(2)原式=(a2+4)2﹣(4a)2
=(a2+4+4a)(a2+4﹣4a)
=(a+2)2(a﹣2)2.
11.解:(1)原式=a(x2﹣4x+4)
=a(x﹣2)2;
(2)原式=x2(m﹣n)﹣y2(m﹣n)
=(m﹣n)(x2﹣y2)
=(m﹣n)(x+y)(x﹣y);
(3)原式=x2+6x+8﹣3
=x2+6x+5
=(x+1)(x+5);
(4)原式=[3(a+b)+(a﹣b)][3(a+b)﹣(a﹣b]
=(4a+2b)(2a+4b)
=4(2a+b)(a+2b).
12.解:(1)∵m﹣n=4,mn=﹣3,
∴m2+n2
=(m﹣n)2+2mn
=42+2×(﹣3)
=16﹣6
=10;
(2)(m2﹣4)(n2﹣4)
=(mn)2﹣4(m2+n2)+16,
当mn=﹣3,m2+n2=10时,
原式=(﹣3)2﹣4×10+16
=9﹣40+16
=﹣15;
(3)8m 32n÷4m+2n
=(23)m (25)n÷(22)m+2n
=23m 25n÷22m+4n
=23m+5n÷22m+4n
=23m+5n﹣2m﹣4n
=2m+n,
∵m﹣n=4,mn=﹣3
∴(m+n)2
=(m﹣n)2+4mn
=42+4×(﹣3)
=16﹣12
=4,
∴m+n=2或﹣2,
∴2m+n
=22或2﹣2
=4或.
13.解:(1)x2+4y2+3xy
=x2+4y2+4xy﹣xy
=(x+2y)2﹣xy
∵x+2y=4,xy=1,
∴原式=42﹣1
=15.
(2)m3+2m2+2022
=m(m2+m)+m2+2022
∵m2+m﹣1=0,
∴m2+m=1
原式=m+m2+2022
=1+2022
=2023
14.解:(1)S1=a2﹣b2,S2=(a+b)(a﹣b),
∵S1=S2,
∴a2﹣b2=(a+b)(a﹣b).
(2)①(﹣x﹣y)(y﹣x)=(﹣x)2﹣y2=x2﹣y2;
②102×98=(100+2)×(100﹣2)=9996.
(3)(3+1)×(32+1)×(34+1)×(38+1)×(316+1)......×(31024+1)+1,
=(3﹣1)×[(3+1)×(32+1)×(34+1)×(38+1)×(316+1)......×(31024+1)]÷(3﹣1)+1,
=(32﹣1)×(32+1)×(34+1)×(38+1)×(316+1)......×(31024+1)÷2+1,
=[(31024)2﹣12]÷2+1,
=(32048﹣1)÷2+1,
=.
15.解:(1)方法1:两个阴影部分的面积和就是边长为a的正方形,与边长为b的正方形的面积和,即a2+b2;
方法2:两个阴影部分的面积和也可以看作从边长为a+b的正方形面积中减去两个长为a,宽为b的长方形面积,即(a+b)2﹣2ab;
故答案为:a2+b2,(a+b)2﹣2ab;
(2)由(1)得,a2+b2=(a+b)2﹣2ab;
(3)①∵m+n=5,
∴(m+n)2=25=m2+2mn+n2,
∵m2+n2=20,
∴2mn=5,
即mn=;
(m﹣n)2=m2﹣2mn+n2=20﹣5=15,
答:mn=,(m﹣n)2=15;
②设a=x﹣2021,b=x﹣2023,则a﹣b=2,a2+b2=(x﹣2021)2+(x﹣2023)2=74,
所以ab===35,
即(x﹣2021)(x﹣2023)=35,
所以[(x﹣2022)+1][(x﹣2022)﹣1]=(x﹣2022)2﹣1=35,
即(x﹣2022)2=36.
16.解:(1)图1中,由图可知S大正方形=(a+b)2,
S组成大正方形的四部分的面积之和=a2+b2+2ab,
由题意得,S大正方形=S组成大正方形的四部分的面积之和,
即(a+b)2=a2+b2+2ab,
故答案为:(a+b)2=a2+b2+2ab.
图2中,由图可知S大正方形=(a+b)2,S小正方形=(a﹣b)2,S四个长方形=4ab,
由题图可知,S大正方形=S小正方形+S四个长方形,
即(a+b)2=(a﹣b)2+4ab,
故答案为:(a+b)2=(a﹣b)2+4ab.
(2)∵(x+y)2=x2+y2+2xy,
∴xy=【(x+y)2﹣(x2+y2)】
∵x+y=8,x2+y2=40,
∴xy=(64﹣40)
=12.
(3)①由图2可得(2m﹣3n)2=(2m+3n)2﹣24mn,
∵2m+3n=5,mn=1,
∴(2m﹣3n)2=52﹣24=1,
∴2m﹣3n=±1.
故答案为:±1.
②由图1可得【(4﹣m)﹣(5﹣m)】2=(4﹣m)2+(5﹣m)2﹣2(4﹣m)(5﹣m),
∴(4﹣m)2+(5﹣m)2=【(4﹣m)﹣(5﹣m)】2+2(4﹣m)(5﹣m),
∵(4﹣m)(5﹣m)=6,
∴原式=1+2×6=13.
故答案为:13.
(4)由题意得AB=AC+CB,
∵AB=7,
∴AC+CB=7,
∵S1+S2=16,
∴AC2+CB2=16,
∵(AC+BC)2=AC2+CB2+2AC CB,
∴AC CB=[(AC+CB)2﹣(AC2+CB2)]
=(49﹣16)
=,
∴S阴影=CD CB=AC CB=.
即图中阴影部分的面积为.
17.解:(1)m2﹣4m﹣5=m2﹣4m+4﹣4﹣5=(m﹣2)2﹣9=(m﹣2+3)(m﹣2﹣3)=(m+1)(m﹣5).
故答案为:(m+1)(m﹣5).
(2)x2﹣6x+12=x2﹣6x+9+3=(x﹣3)2+3;
∴x2﹣6x+12的最小值是3.
故答案为;3.
(3)y=﹣x2+2x﹣3,
y=﹣x2+2x﹣1﹣2,
y=﹣(x+1)2﹣2,
∴当x=﹣1的时候,y有最大值﹣2.
故答案为:若y=﹣x2+2x﹣3,当x=﹣1时,y有最大值,这个值是﹣2.
(4 a2+b2+c2﹣6a﹣10b﹣8c+50=0,
a2﹣6a+9+b2﹣10b+25+c2﹣8c+16=0,
(a﹣3)2+(b﹣5)2+(c﹣4)2=0,
三个完全平方式子的和为0,所以三个完全平方式子分别等于0.
a﹣3=0,b﹣5=0,c﹣4=0,
得,a=3,b=5,c=4.
∴△ABC是直角三角形.
故答案为:△ABC是直角三角形.
18.解:(1)方法1:大正方形的边长为(a+b),
∴S=(a+b)2;
方法2:大正方形=各个部分相加之和,
∴S=a2+2ab+b2.
故答案为:(a+b)2,a2+2ab+b2.
(2)由图2可得总面积减掉两个小矩形面积等于两个正方形面积之和,
即(a+b)2﹣2ab=a2+b2.
故答案为:(a+b)2=a2+b2+2ab.
(3)①∵a+b=5,
∴(a+b)2=25,
a2+b2=21,
∴2ab=(a+b)2﹣(a2+b2)=25﹣21=4,
∴ab=2.
②设m=2022﹣a,n=a﹣2020,
则m+n=2,m2+n2=(2022﹣a)2+(a﹣2020)2=10,
由(m+n)2=m2+n2+2mn得,
4=10+2mn,
∴mn=﹣3,
(2022﹣a)(a﹣2020)=mn=﹣3,
即(2022﹣a)(a﹣2020)的值为﹣3.
19.解:(1)若要拼出一个面积为(a+2b)(a+b)的矩形,则需要A号卡片1张,B号卡片2张,C号卡片3张.
故答案为:3.
(2)①∵(a+b)2=a2+b2+2ab,
∴2ab+14=36,
∴ab=11;
②(x﹣2020)2+(x﹣2022)2=10,
∵[(x﹣2020)﹣(x﹣2022)]2=(x﹣2020)2+(x﹣2022)2﹣2(x﹣2020)(x﹣2022),
∴4=10﹣2(x﹣2020)(x﹣2022),
∴2(x﹣2020)(x﹣2022)=6,
∵[(x﹣2020)+(x﹣2022)]2=(x﹣2020)2+(x﹣2022)2+2(x﹣2020)(x﹣2022),
∴[2(x﹣2021)]2=10+6=16,即4(x﹣2021)2=16,
∴(x﹣2021)2=4.
20.解:(1)∵(3a+2b)×(2a+b)=(6a2+7ab+2b2)平方米,
∴长方形地块的面积为(6a2+7ab+2b2)平方米;
(2)∵(2a﹣b)×2b=(4ab﹣2b2)平方米,
∴雕像的面积为(4ab﹣2b2)平方米;
(3)∵绿化部分的面积为6a2+7ab+2b2﹣(4ab﹣2b2)=(6a2+3ab+4b2)平方米;
∴当a=100,b=40时,
6a2+3ab+4b2
=6×100×100+3×100×40+4×40×40
=78400(平方米),
∴绿化部分的面积为78400平方米.
