2022-2023学年北师大版八年级数学上册 7.5 三角形的内角和定理 同步练习(word、含答案)
文档属性
| 名称 | 2022-2023学年北师大版八年级数学上册 7.5 三角形的内角和定理 同步练习(word、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 132.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 22:11:41 | ||
图片预览

文档简介
(北师大版)八年级上册 7.5 三角形的内角和定理 同步练习
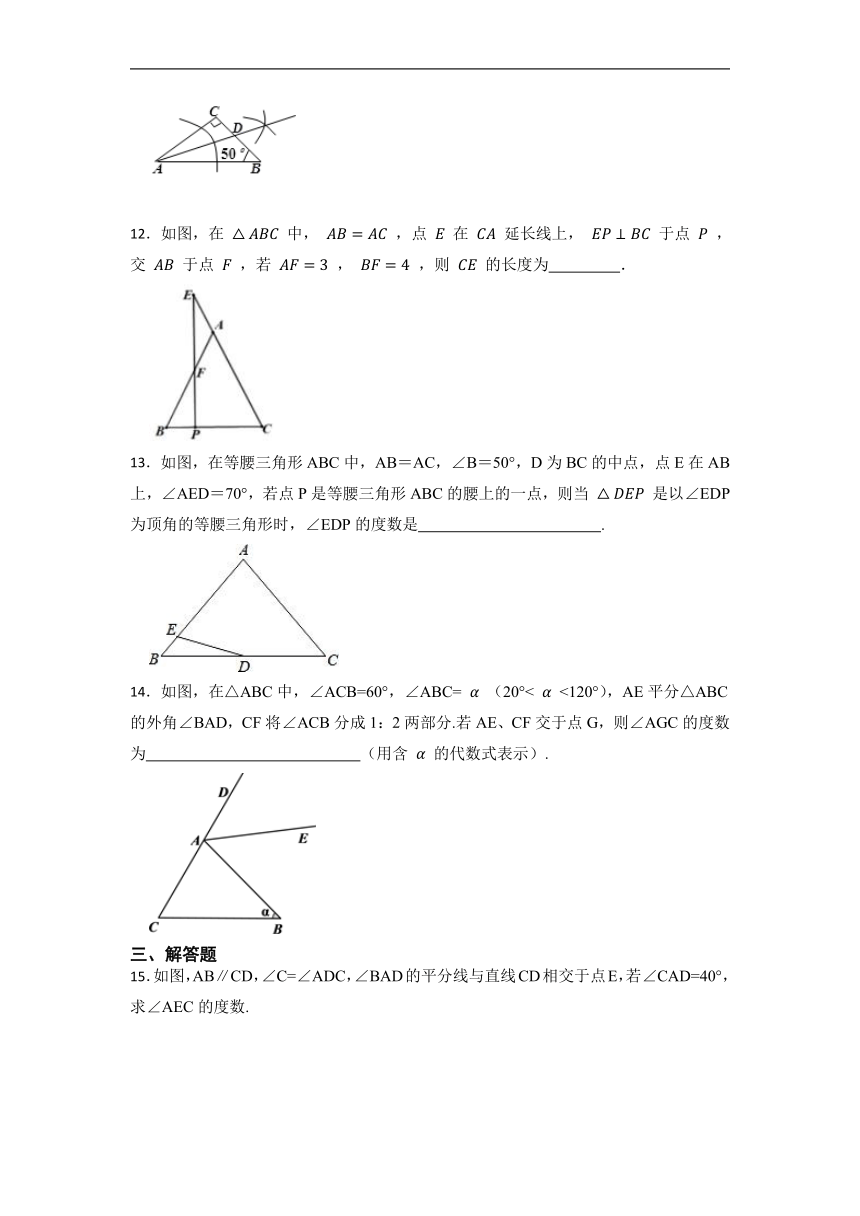
一、单选题
1.已知等腰三角形的一个角为72°,则其顶角为( )
A.36° B.72° C.72°或36° D.无法确定
2.三角形中,若一个角等于其他两个角的和,则这个三角形是( )
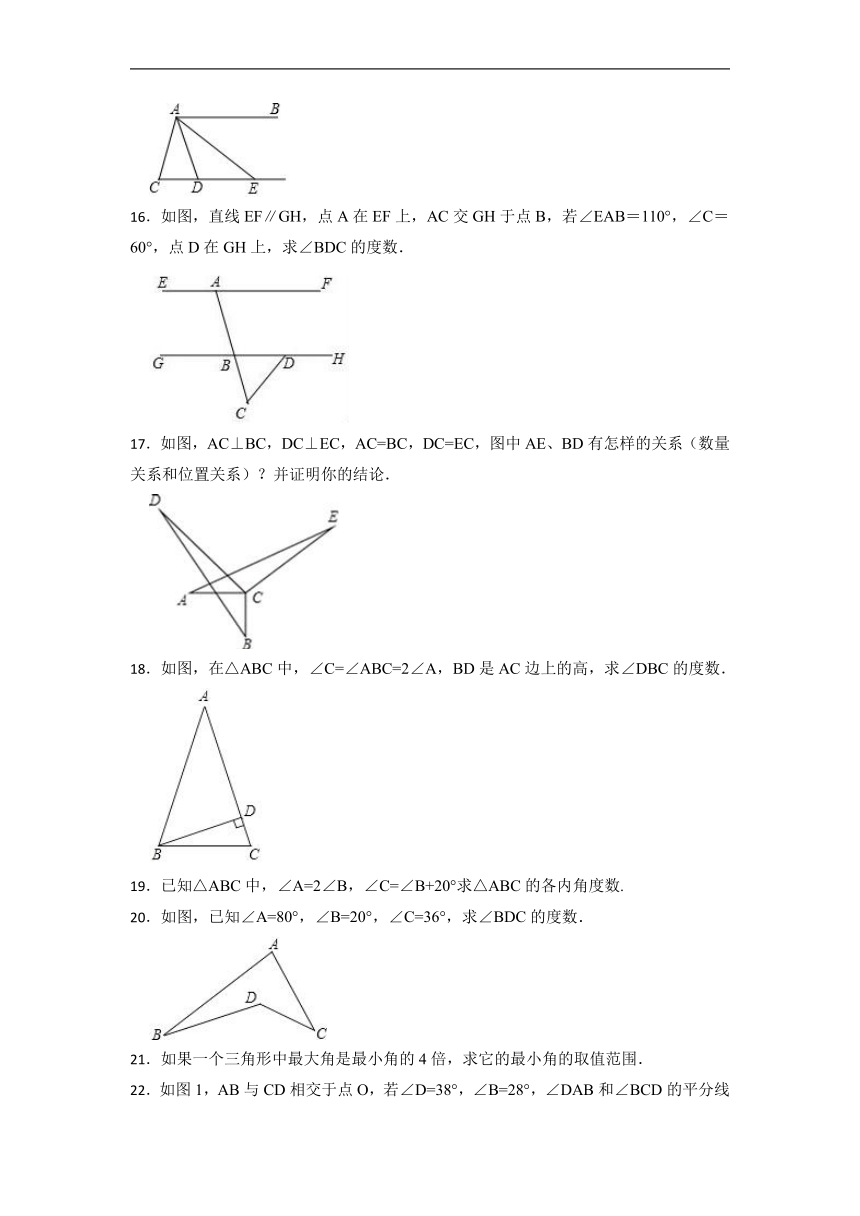
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等腰三角形
3.如图,OA=OB,OC=OD,∠O=50°,∠D=30°,则∠AEC等于( )
A.70° B.50° C.45° D.60°
4.如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于点G,若∠BDC=140°,∠BGC=110°,则∠A的度数为( )
A.50 B.55 C.70 D.80
5.在△ABC中,∠A=∠B=∠C,则△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.以上都不对
6.如图,在△ABC中,∠C=90°.若BD∥AE,∠DBC=20°,则∠CAE的度数是( )
A.40° B.60° C.70° D.80
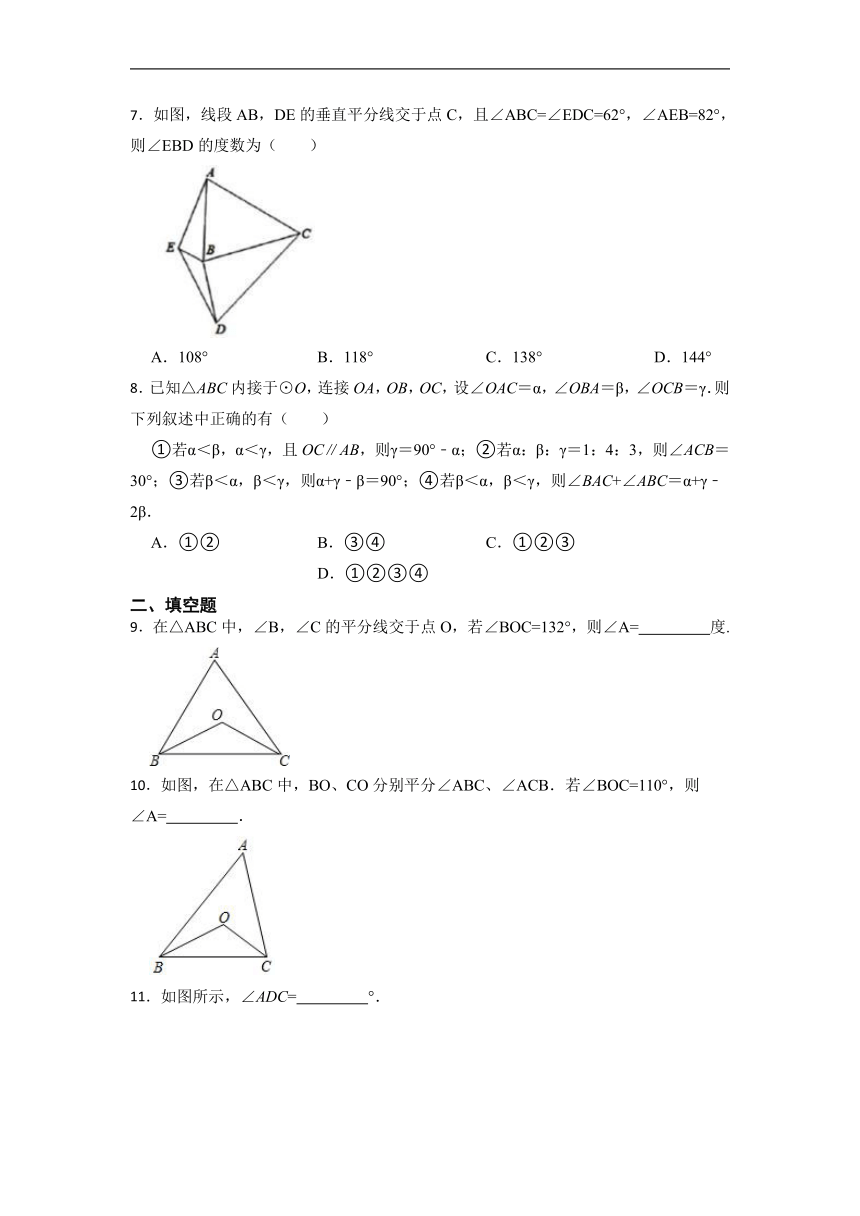
7.如图,线段AB,DE的垂直平分线交于点C,且∠ABC=∠EDC=62°,∠AEB=82°,则∠EBD的度数为( )
A.108° B.118° C.138° D.144°
8.已知△ABC内接于⊙O,连接OA,OB,OC,设∠OAC=α,∠OBA=β,∠OCB=γ.则下列叙述中正确的有( )
①若α<β,α<γ,且OC∥AB,则γ=90°﹣α;②若α:β:γ=1:4:3,则∠ACB=30°;③若β<α,β<γ,则α+γ﹣β=90°;④若β<α,β<γ,则∠BAC+∠ABC=α+γ﹣2β.
A.①② B.③④ C.①②③ D.①②③④
二、填空题
9.在△ABC中,∠B,∠C的平分线交于点O,若∠BOC=132°,则∠A= 度.
10.如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A= .
11.如图所示,∠ADC= °.
12.如图,在 中, ,点 在 延长线上, 于点 ,交 于点 ,若 , ,则 的长度为 .
13.如图,在等腰三角形ABC中,AB=AC,∠B=50°,D为BC的中点,点E在AB上,∠AED=70°,若点P是等腰三角形ABC的腰上的一点,则当 是以∠EDP为顶角的等腰三角形时,∠EDP的度数是 .
14.如图,在△ABC中,∠ACB=60°,∠ABC= (20°< <120°),AE平分△ABC的外角∠BAD,CF将∠ACB分成1:2两部分.若AE、CF交于点G,则∠AGC的度数为 (用含 的代数式表示).
三、解答题
15.如图,AB∥CD,∠C=∠ADC,∠BAD的平分线与直线CD相交于点E,若∠CAD=40°,求∠AEC的度数.
16.如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠EAB=110°,∠C=60°,点D在GH上,求∠BDC的度数.
17.如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,图中AE、BD有怎样的关系(数量关系和位置关系)?并证明你的结论.
18.如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.
19.已知△ABC中,∠A=2∠B,∠C=∠B+20°求△ABC的各内角度数.
20.如图,已知∠A=80°,∠B=20°,∠C=36°,求∠BDC的度数.
21.如果一个三角形中最大角是最小角的4倍,求它的最小角的取值范围.
22.如图1,AB与CD相交于点O,若∠D=38°,∠B=28°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求:
(1)∠P的度数;
(2)设∠D=α,∠B=β,∠DAP= ∠DAB,∠DCP= ∠DCB,其他条件不变,如图2,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),直接写出结论.
参考答案
1.C
2.B
3.A
4.D
5.C
6.C
7.A
8.A
9.84
10.40°
11.70°
12.10
13.40°或100°或140°
14. 或
15.解:∵∠C=∠ADC,∠CAD=40°,∴∠C=70°.
∵AB∥CD,∴∠CAB=110°,∴∠DAB=110°﹣40°=70°.
∵AE是∠BAD的平分线,∴∠BAE=35°.
∵AB∥CD,∴∠AEC=35°.
16.解:∵EF∥GH,
∴∠CBG=∠EAB,
∵∠EAB=110°,
∴∠CBG=110°,
∴∠CBD=180°﹣∠CBG=70°,
在△BCD中,∵∠C=60°,
∴∠BDC=180°﹣∠C﹣∠CBD=180°﹣60°﹣70°=50°,
即:∠BDC的度数为50°
17.解:结论:AE=BD,AE⊥BD.理由如下: 如图,设AC交BD于N,AE交BD于O. ∵AC⊥BC,DC⊥EC,∴∠ACB=∠DCE=90°,∴∠DCB=∠ECA. 在△DCB和△ECA中,∵ ,∴△DCB≌△ECA(SAS),∴∠A=∠B,BD=AE. ∵∠AND=∠BNC,∠B+∠BNC=90°,∴∠A+∠AND=90°,∴∠AON=90°,∴BD⊥AE.
18.解:∵∠C=∠ABC=2∠A,
∴∠C+∠ABC+∠A=5∠A=180°,
∴∠A=36°.
则∠C=∠ABC=2∠A=72°.
又BD是AC边上的高,
则∠DBC=90°-∠C=18°
19.解:在ΔABC中, ∠A=2∠B,∠C=∠B+20°,
设∠B = x , 则∠A=2 x , ∠C= x +20 ,
∠A+∠B+∠C=180 ,得x+(x+20)+2x=180,
解得x=40
∠A=80 , ∠B=40 , ∠C=60 .
故答案为:
∠A=80 , ∠B=40 , ∠C=60
20.解:连接AD,并延长,
∵∠3=∠1+∠B,∠4=∠2+∠C.
∴∠BDC=∠3+∠4=(∠1+∠B)+(∠2+∠C)=∠B+∠BAC+∠C.
∵∠A=80°,∠B=20°,∠C=36°.
∴∠BDC=136°
21.解:设∠A是它的最小角,∠C是最大角,∠B是中间的角,则∠A≤∠B≤∠C,又∠C=4∠A.由可得∠A+∠A+4∠A≤180°,即么A≤30°.可得∠A+4∠A+4∠A≥180°,即∠A≥20°.所以最小角的取值范围为20°≤4≤30°.
22.(1)解:根据三角形的内角和定理,∠DAP+∠D=∠DCP+∠P,
∴∠DAP-∠DCP=∠P-∠D,
∠DAO+∠D=∠BCO+∠B,
∴∠DAO-∠BCO=∠B-∠D,
∵AP、CP分别为∠DAB和∠BCD的平分线,
∴∠DAO=2∠DAP,∠BCO=2∠DCP,
∴∠DAO-∠BCO=2(∠DAP-∠DCP),
∴∠B-∠D=2(∠P-∠D),
整理得,∠P= (∠B+∠D),
∵∠D=38°,∠B=28°,
∴∠P= (38°+28°)=33°
(2)解:根据三角形的内角和定理,∠DAP+∠D=∠DCP+∠P,
∴∠DAP-∠DCP=∠P-∠D,
∠DAO+∠D=∠BCO+∠B,
∴∠DAO-∠BCO=∠B-∠D,
∵∠DAP= ∠DAB,∠DCP= ∠DCB,
∴∠DAO-∠BCO=3(∠DAP-∠DCP),
∴∠B-∠D=3(∠P-∠D),
整理得,∠P= (∠B+2∠D),
∵∠D=α,∠B=β,
∴∠P= (β+2α)
一、单选题
1.已知等腰三角形的一个角为72°,则其顶角为( )
A.36° B.72° C.72°或36° D.无法确定
2.三角形中,若一个角等于其他两个角的和,则这个三角形是( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等腰三角形
3.如图,OA=OB,OC=OD,∠O=50°,∠D=30°,则∠AEC等于( )
A.70° B.50° C.45° D.60°
4.如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于点G,若∠BDC=140°,∠BGC=110°,则∠A的度数为( )
A.50 B.55 C.70 D.80
5.在△ABC中,∠A=∠B=∠C,则△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.以上都不对
6.如图,在△ABC中,∠C=90°.若BD∥AE,∠DBC=20°,则∠CAE的度数是( )
A.40° B.60° C.70° D.80
7.如图,线段AB,DE的垂直平分线交于点C,且∠ABC=∠EDC=62°,∠AEB=82°,则∠EBD的度数为( )
A.108° B.118° C.138° D.144°
8.已知△ABC内接于⊙O,连接OA,OB,OC,设∠OAC=α,∠OBA=β,∠OCB=γ.则下列叙述中正确的有( )
①若α<β,α<γ,且OC∥AB,则γ=90°﹣α;②若α:β:γ=1:4:3,则∠ACB=30°;③若β<α,β<γ,则α+γ﹣β=90°;④若β<α,β<γ,则∠BAC+∠ABC=α+γ﹣2β.
A.①② B.③④ C.①②③ D.①②③④
二、填空题
9.在△ABC中,∠B,∠C的平分线交于点O,若∠BOC=132°,则∠A= 度.
10.如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A= .
11.如图所示,∠ADC= °.
12.如图,在 中, ,点 在 延长线上, 于点 ,交 于点 ,若 , ,则 的长度为 .
13.如图,在等腰三角形ABC中,AB=AC,∠B=50°,D为BC的中点,点E在AB上,∠AED=70°,若点P是等腰三角形ABC的腰上的一点,则当 是以∠EDP为顶角的等腰三角形时,∠EDP的度数是 .
14.如图,在△ABC中,∠ACB=60°,∠ABC= (20°< <120°),AE平分△ABC的外角∠BAD,CF将∠ACB分成1:2两部分.若AE、CF交于点G,则∠AGC的度数为 (用含 的代数式表示).
三、解答题
15.如图,AB∥CD,∠C=∠ADC,∠BAD的平分线与直线CD相交于点E,若∠CAD=40°,求∠AEC的度数.
16.如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠EAB=110°,∠C=60°,点D在GH上,求∠BDC的度数.
17.如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,图中AE、BD有怎样的关系(数量关系和位置关系)?并证明你的结论.
18.如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.
19.已知△ABC中,∠A=2∠B,∠C=∠B+20°求△ABC的各内角度数.
20.如图,已知∠A=80°,∠B=20°,∠C=36°,求∠BDC的度数.
21.如果一个三角形中最大角是最小角的4倍,求它的最小角的取值范围.
22.如图1,AB与CD相交于点O,若∠D=38°,∠B=28°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求:
(1)∠P的度数;
(2)设∠D=α,∠B=β,∠DAP= ∠DAB,∠DCP= ∠DCB,其他条件不变,如图2,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),直接写出结论.
参考答案
1.C
2.B
3.A
4.D
5.C
6.C
7.A
8.A
9.84
10.40°
11.70°
12.10
13.40°或100°或140°
14. 或
15.解:∵∠C=∠ADC,∠CAD=40°,∴∠C=70°.
∵AB∥CD,∴∠CAB=110°,∴∠DAB=110°﹣40°=70°.
∵AE是∠BAD的平分线,∴∠BAE=35°.
∵AB∥CD,∴∠AEC=35°.
16.解:∵EF∥GH,
∴∠CBG=∠EAB,
∵∠EAB=110°,
∴∠CBG=110°,
∴∠CBD=180°﹣∠CBG=70°,
在△BCD中,∵∠C=60°,
∴∠BDC=180°﹣∠C﹣∠CBD=180°﹣60°﹣70°=50°,
即:∠BDC的度数为50°
17.解:结论:AE=BD,AE⊥BD.理由如下: 如图,设AC交BD于N,AE交BD于O. ∵AC⊥BC,DC⊥EC,∴∠ACB=∠DCE=90°,∴∠DCB=∠ECA. 在△DCB和△ECA中,∵ ,∴△DCB≌△ECA(SAS),∴∠A=∠B,BD=AE. ∵∠AND=∠BNC,∠B+∠BNC=90°,∴∠A+∠AND=90°,∴∠AON=90°,∴BD⊥AE.
18.解:∵∠C=∠ABC=2∠A,
∴∠C+∠ABC+∠A=5∠A=180°,
∴∠A=36°.
则∠C=∠ABC=2∠A=72°.
又BD是AC边上的高,
则∠DBC=90°-∠C=18°
19.解:在ΔABC中, ∠A=2∠B,∠C=∠B+20°,
设∠B = x , 则∠A=2 x , ∠C= x +20 ,
∠A+∠B+∠C=180 ,得x+(x+20)+2x=180,
解得x=40
∠A=80 , ∠B=40 , ∠C=60 .
故答案为:
∠A=80 , ∠B=40 , ∠C=60
20.解:连接AD,并延长,
∵∠3=∠1+∠B,∠4=∠2+∠C.
∴∠BDC=∠3+∠4=(∠1+∠B)+(∠2+∠C)=∠B+∠BAC+∠C.
∵∠A=80°,∠B=20°,∠C=36°.
∴∠BDC=136°
21.解:设∠A是它的最小角,∠C是最大角,∠B是中间的角,则∠A≤∠B≤∠C,又∠C=4∠A.由可得∠A+∠A+4∠A≤180°,即么A≤30°.可得∠A+4∠A+4∠A≥180°,即∠A≥20°.所以最小角的取值范围为20°≤4≤30°.
22.(1)解:根据三角形的内角和定理,∠DAP+∠D=∠DCP+∠P,
∴∠DAP-∠DCP=∠P-∠D,
∠DAO+∠D=∠BCO+∠B,
∴∠DAO-∠BCO=∠B-∠D,
∵AP、CP分别为∠DAB和∠BCD的平分线,
∴∠DAO=2∠DAP,∠BCO=2∠DCP,
∴∠DAO-∠BCO=2(∠DAP-∠DCP),
∴∠B-∠D=2(∠P-∠D),
整理得,∠P= (∠B+∠D),
∵∠D=38°,∠B=28°,
∴∠P= (38°+28°)=33°
(2)解:根据三角形的内角和定理,∠DAP+∠D=∠DCP+∠P,
∴∠DAP-∠DCP=∠P-∠D,
∠DAO+∠D=∠BCO+∠B,
∴∠DAO-∠BCO=∠B-∠D,
∵∠DAP= ∠DAB,∠DCP= ∠DCB,
∴∠DAO-∠BCO=3(∠DAP-∠DCP),
∴∠B-∠D=3(∠P-∠D),
整理得,∠P= (∠B+2∠D),
∵∠D=α,∠B=β,
∴∠P= (β+2α)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
