2022-2023学年北师大版九年级数学上册4.5相似三角形判定定理的证明 选择题 提升训练(Word版含答案)
文档属性
| 名称 | 2022-2023学年北师大版九年级数学上册4.5相似三角形判定定理的证明 选择题 提升训练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 466.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-16 07:46:31 | ||
图片预览


文档简介
2022-2023学年北师大版九年级数学上册《4.5相似三角形判定定理的证明》
选择题专题提升训练(附答案)
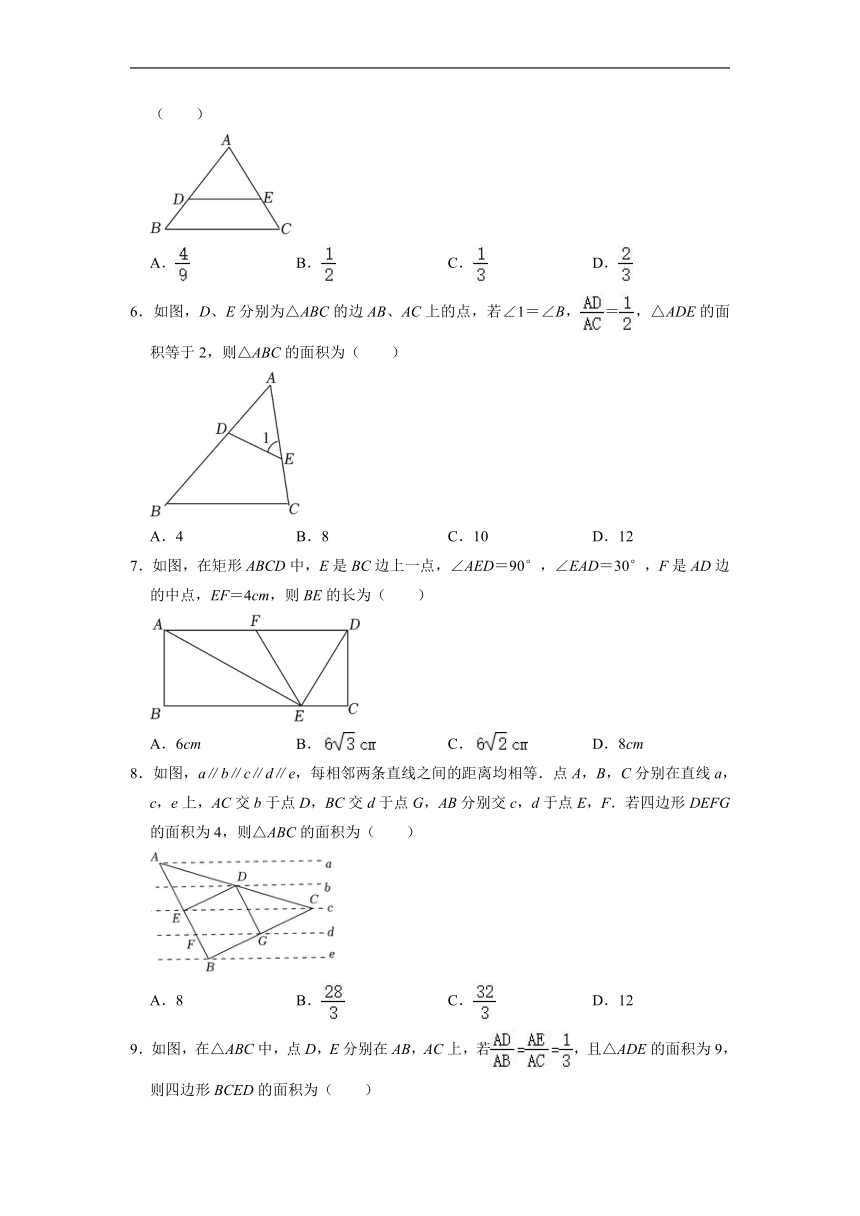
1.如图,在△ABC中,点D、E分别是线段AB、AC的中点,若S△ADE=2,则四边形BCED的面积是( )
A.4 B.6 C.8 D.10
2.如图,AB∥CD,AC,BD相交于点E,AE=1,EC=2,DE=3,则BD的长为( )
A. B.4 C. D.6
3.如图,菱形ABCD中,点E是边CD的中点,EF垂直AB交AB的延长线于点F,若BF:CE=1:2,EF=,则菱形ABCD的边长是( )
A.3 B.4 C.5 D.
4.如图,在Rt△ABC纸片中,∠ACB=90°,AC=4,BC=3,点D,E分别在BC、AB边上,连接DE,将△BDE沿DE翻折,使点B落在点F的位置,连接AF,若四边形BEFD是菱形,则AF的长的最小值为( )
A. B. C. D.
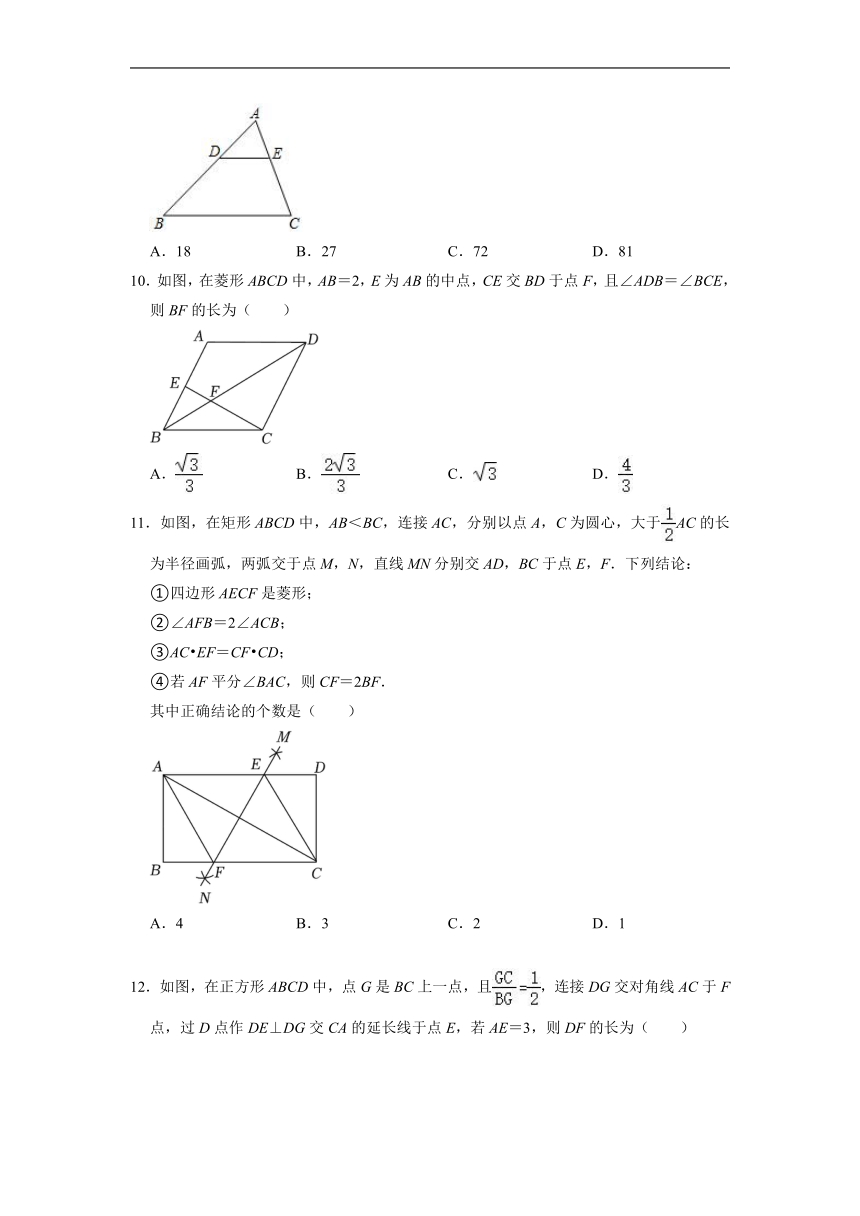
5.如图,在△ABC中,D,E分别是AB和AC上的点,DE∥BC,若=,那么=( )
A. B. C. D.
6.如图,D、E分别为△ABC的边AB、AC上的点,若∠1=∠B,=,△ADE的面积等于2,则△ABC的面积为( )
A.4 B.8 C.10 D.12
7.如图,在矩形ABCD中,E是BC边上一点,∠AED=90°,∠EAD=30°,F是AD边的中点,EF=4cm,则BE的长为( )
A.6cm B. C. D.8cm
8.如图,a∥b∥c∥d∥e,每相邻两条直线之间的距离均相等.点A,B,C分别在直线a,c,e上,AC交b于点D,BC交d于点G,AB分别交c,d于点E,F.若四边形DEFG的面积为4,则△ABC的面积为( )
A.8 B. C. D.12
9.如图,在△ABC中,点D,E分别在AB,AC上,若,且△ADE的面积为9,则四边形BCED的面积为( )
A.18 B.27 C.72 D.81
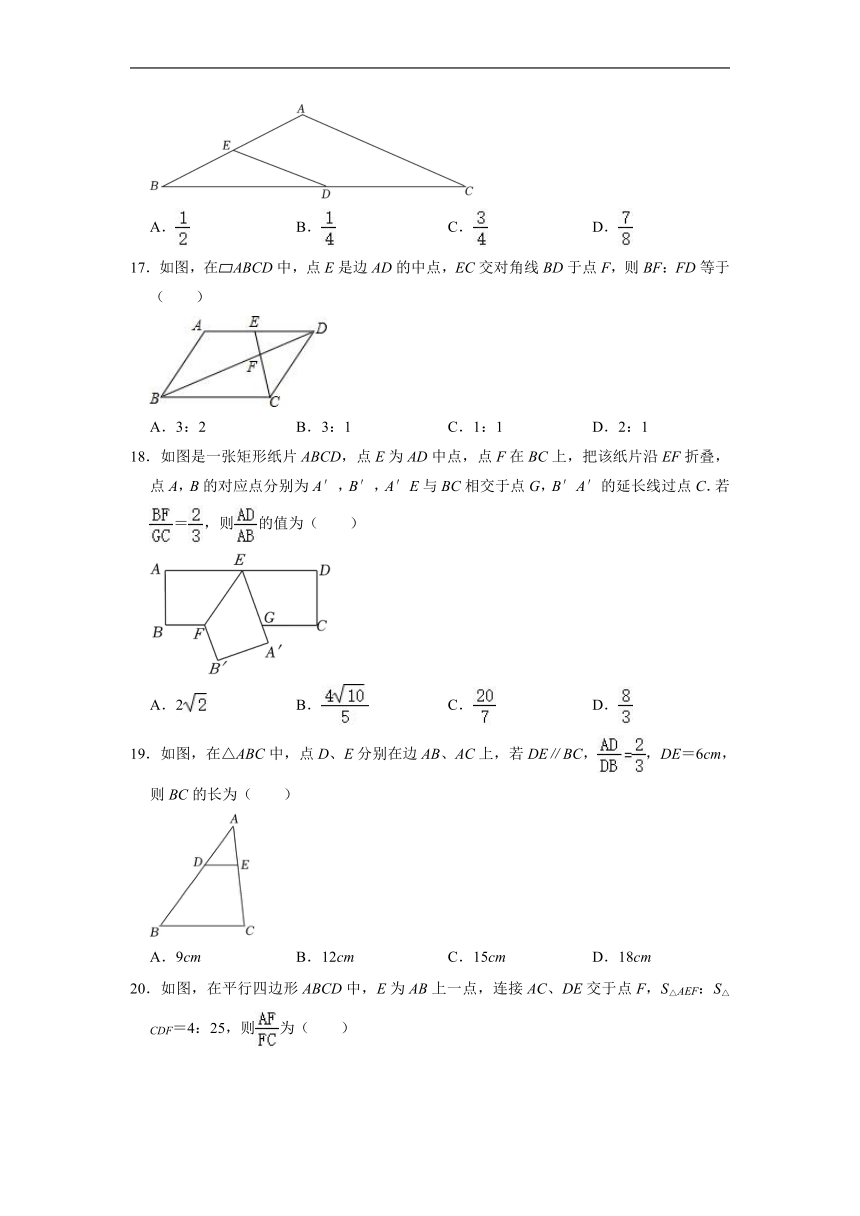
10.如图,在菱形ABCD中,AB=2,E为AB的中点,CE交BD于点F,且∠ADB=∠BCE,则BF的长为( )
A. B. C. D.
11.如图,在矩形ABCD中,AB<BC,连接AC,分别以点A,C为圆心,大于AC的长为半径画弧,两弧交于点M,N,直线MN分别交AD,BC于点E,F.下列结论:
①四边形AECF是菱形;
②∠AFB=2∠ACB;
③AC EF=CF CD;
④若AF平分∠BAC,则CF=2BF.
其中正确结论的个数是( )
A.4 B.3 C.2 D.1
12.如图,在正方形ABCD中,点G是BC上一点,且,连接DG交对角线AC于F点,过D点作DE⊥DG交CA的延长线于点E,若AE=3,则DF的长为( )
A.2 B. C. D.
13.如图,等腰△ABC的面积为2,AB=AC,BC=2.作AE∥BC且AE=BC.点P是线段AB上一动点,连结PE,过点E作PE的垂线交BC的延长线于点F,M是线段EF的中点.那么,当点P从A点运动到B点时,点M的运动路径长为( )
A. B.3 C.2 D.4
14.如图,在△ABC中,AB<AC,将△ABC以点A为中心逆时针旋转得到△ADE,点D在BC边上,DE交AC于点F.下列结论:①△AFE∽△DFC;②DA平分∠BDE;③∠CDF=∠BAD,其中所有正确结论的序号是( )
A.①② B.②③ C.①③ D.①②③
15.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=2:3,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A.2:3 B.2:5 C.4:25 D.4:9
16.如图,在△ABC中,D、E分别为线段BC、BA的中点,设△ABC的面积为S1,△EBD的面积为S2,则=( )
A. B. C. D.
17.如图,在 ABCD中,点E是边AD的中点,EC交对角线BD于点F,则BF:FD等于( )
A.3:2 B.3:1 C.1:1 D.2:1
18.如图是一张矩形纸片ABCD,点E为AD中点,点F在BC上,把该纸片沿EF折叠,点A,B的对应点分别为A′,B′,A′E与BC相交于点G,B′A′的延长线过点C.若=,则的值为( )
A.2 B. C. D.
19.如图,在△ABC中,点D、E分别在边AB、AC上,若DE∥BC,,DE=6cm,则BC的长为( )
A.9cm B.12cm C.15cm D.18cm
20.如图,在平行四边形ABCD中,E为AB上一点,连接AC、DE交于点F,S△AEF:S△CDF=4:25,则为( )
A.2:5 B.5:2 C.2:7 D.4:25
21.如图,正方形ABCD与正方形BEFG有公共顶点B,连接EC、GA,交于点O,GA与BC交于点P,连接OD、OB,则下列结论一定正确的是( )
①EC⊥AG;②△OBP∽△CAP;③OB平分∠CBG;④∠AOD=45°;
A.①③ B.①②③ C.②③ D.①②④
22.如图,在平行四边形ABCD中,点F在BA的延长线上,连接CF交AD于E,交BD于G,下列结论错误的是( )
A.= B.= C.= D.=
参考答案
1.解:∵点D、E分别是线段AB、AC的中点,
∴DE∥BC,DE:BC=1:2,
∴△ADE∽△ABC,
∵S△ADE=2,
∴S△ABC=2÷=8,
∴四边形BCED的面积是8﹣2=6,
故选:B.
2.解:∵AB∥CD,
∴△ABE∽△CDE,
∴=,即=,
∴BE=1.5,
∴BD=BE+DE=4.5.
故选:C.
3.解:过点D作DH⊥AB于点H,如图,
∵四边形ABCD是菱形,
∴AD=AB=CD,AB∥CD.
∵EF⊥AB,DH⊥AB,
∴DH∥EF,
∴四边形DHFE为平行四边形,
∴HF=DE,DH=EF=.
∵点E是边CD的中点,
∴DE=CD,
∴HF=CD=AB.
∵BF:CE=1:2,
∴设BF=x,则CE=2x,
∴CD=4x,DE=HF=2x,
AD=AB=4x,
∴AF=AB+BF=5x.
∴AH=AF﹣HF=3x.
在Rt△ADH中,
∵DH2+AH2=AD2,
∴.
解得:x=±1(负数不合题意,舍去),
∴x=1.
∴AB=4x=4.
即菱形ABCD的边长是4,
故选:B.
4.解:如图,连接BF交ED于点O,设EF与AC交于点G,
∵四边形BEFD是菱形,
∴BF平分∠ABC,
∴点F在∠ABC的平分线上运动,
∴当AF⊥BF时,AF的长最小.
在菱形BEFD中,BF⊥ED,OB=OF,EF∥BC,
∴EO∥AF,
∴△BEO∽△BAF,
∴===,
∴BE=AB=AE.
在Rt△ABC中,AC=4,BC=3,
∴AB=5,
∴BE=AE=2.5,
∵AF⊥BF.
∴EF=2.5,
∵EF∥BC,
∴△AGE∽△ACB,
∴===,∠AGE=∠ACB=90°,
∴EG=BC=1.5,AG=AC=2,
∴GF=EF﹣EG=1.
∵∠AGF=∠AGE=90°,
∴AF===.
故选:A.
5.解:∵DE∥BC,
∴△ADE∽△ABC,
∴=,
∵=,
∴=,
∴==.
故选:D.
6.解:∵∠1=∠B,∠A=∠A,
∴△ADE∽△ACB,
∵=,
∴=,
∵△ADE的面积等于2,
∴△ACB的面积等于8.
故选:B.
7.解:∵∠AED=90°,F是AD边的中点,
∴EF=AF=DF=AD=4,
∴AD=8,
∵∠AED=90°,∠EAD=30°,
∴DE=AD=4,
∴AE===4,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AEB=∠EAD=30°,
∵cos∠AEB=,
∴BE=AE cos30°=4×=6(cm),
故选:A.
8.解:由图象可得,点D,E,F,G分别为AC,AB,EB,BC的中点,
∴DG,DE,FG分别为△CAB,△ABC,△BEC的中位线,
∴S△CDG=S△AED=S△ABC,S△BFG=S△BEC=S△ABC,
∵四边形DEFG的面积为4,
∴S△ABC﹣S△CDG﹣S△AED﹣S△BFG=S△ABC=4,
∴S△ABC=.
故选:C.
9.解:∵,∠A=∠A,
∴△ADE∽△ABC,
∴=()2=()2=,
∵△ADE的面积为9,
∴△ABC的面积=81,
∴四边形BCED的面积=△ABC的面积﹣△ADE的面积
=81﹣9
=72,
故选:C.
10.解:∵四边形ABCD是菱形,
∴AD=AB=CD=BC=2,AB∥CD,AD∥BC,
∴∠ADB=∠FBC,
∵∠ADB=∠BCE,
∴∠FBC=∠FCB,
∴FB=FC,
∵E为AB的中点,
∴BE=AB=1,
∵AB∥CD,
∴∠ABF=∠DCE,∠BEF=∠DCE,
∴△BEF∽△DCF,
∴=,
∴FC=2EF,
∴FB=2EF,
设EF=x,则BF=FC=2x,
∴EC=EF+CF=3x,
∵AB=AD,
∴∠ADB=∠ABD,
∴∠ABD=∠BCE,
∵∠BEF=∠BEF,
∴△BEF∽△CEB,
∴,
∴BE2=EF EC,
∴12=x 3x,
∴或x=﹣(舍去),
∴BF=2x=,
故选:B.
11.解:根据题意知,BF垂直平分AC,
在△AOE和△COF中,
,
∴△AOE≌△COF(AAS),
∴OE=OF,
∴AE=AF=CF=CE,
即四边形AECF是菱形,
故①结论正确;
∵∠AFB=∠FAO+∠ACB,AF=FC,
∴∠FAO=∠ACB,
∴∠AFB=2∠ACB,
故②结论正确;
∵S四边形AECF=CF CD=AC OE×2=AC EF,
故③结论不正确;
若AF平分∠BAC,则∠BAF=∠FAC=∠CAD=90°=30°,
∴AF=2BF,
∵CF=AF,
∴CF=2BF,
故④结论正确;
故选:B.
12.解:过点E作EH⊥AD,交DA延长线于H,
∴∠H=90°,
在正方形ABCD中,AB=BC=CD=AD,∠BAD=∠B=∠BCD=∠ADC=90°,
∴∠2+∠3=90°,∠H=∠BCD,
∵DE⊥DG,
∴∠EDG=90°,
∴∠2+∠1=90°,
∴∠1=∠3,
∴△DEH∽△DGC,
∴=,
∵,
∴设GC=x,则BG=2x,DC=BC=3x,
∴=,
∴DH=3EH,
∵AC是正方形ABCD对角线,
∴∠DAC=45°,
∵∠EAH=∠DAC=45°,
∴∠HEA=45°,
∴EH=HA,
∴EH2+HA2=9,
∴EH=HA=,
∴DH=,
∴AD=3,
∴GC=,
∴DG==2,
∵在正方形ABCD中,AD∥BC,
∴==,
∴DF=3GF,
∴DF=;
故选:D.
13.解:如图,过点A作AH⊥BC于点H.
当点P与A重合时,点F与C重合,当点P与B重合时,点F的对应点为F″,
点M的运动轨迹是△ECF″的中位线,M′M″=CF″,
∵AB=AC,AH⊥BC,
∴BH=CH,
∵AE∥BC,AE=BC,
∴AE=CH,
∴四边形AHCE是平行四边形,
∵∠AHC=90°,
∴四边形AHCE是矩形,
∴EC⊥BF″,AH=EC,
∵BC=2,S△ABC=2,
∴×2×AH=2,
∴AH=EC=2,
∵∠BEF″=∠ECB=∠ECF″,
∴∠BEC+∠CEF″=90°,
∠CEF″+∠F″=90°,
∴∠BEC=∠F″,
∴△ECB∽△F″CE,
∴EC2=CB CF″,
∴CF″==6,
∴M′M″=3
故选:B.
14.解:∵将△ABC以点A为中心逆时针旋转得到△ADE,
∴∠BAC=∠DAE,∠B=∠ADE,AB=AD,∠E=∠C,
∴∠B=∠ADB,
∴∠ADE=∠ADB,
∴DA平分∠BDE,
∴②符合题意;
∵∠AFE=∠DFC,∠E=∠C,
∴△AFE∽△DFC,
∴①符合题意;
∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠FAE,
∵△AFE∽△DFC,
∴∠FAE=∠CDF,
∴∠BAD=∠CDF,
∴③符合题意;
故选:D.
15.解:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴△DEF∽△BAF,
∵DE:EC=2:3,
∴DE:DC=2:5,
∴DE:AB=2:5,
∴S△DEF:S△BAF=()2=,
故选:C.
16.解:在△ABC中,D、E分别为线段BC、BA的中点,
∴DE为△ABC的中位线,
∴DE∥AC,DE=AC,
∴△BED∽△BAC,
∵=,
∴=,
即=,
故选:B.
17.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△DEF∽△BCF,
∴BF:FD=BC:DE,
又∵点E是边AD的中点,
∴DE=AD=BC,
∴BF:FD=BC:DE=2:1,
故选:D.
18.解:连接FG,CA′,过点G作GT⊥AD于点T.设AB=x,AD=y.
∵=,
∴可以假设BF=2k,CG=3k.
∵AE=DE=y,
由翻折的性质可知EA=EA′=y,BF=FB′=2k,∠AEF=∠GEF,
∵AD∥CB,
∴∠AEF=∠EFG,
∴∠GEF=∠GFE,
∴EG=FG=y﹣5k,
∴GA′=y﹣(y﹣5k)=5k﹣y,
∵C,A′,B′共线,GA′∥FB′,
∴=,
∴=,
∴y2﹣12ky+32k2=0,
∴y=8k或y=4k(舍去),
∴AE=DE=4k,
∵四边形CDTG是矩形,
∴CG=DT=3k,
∴ET=k,
∵EG=8k﹣5k=3k,
∴AB=CD=GT==2k,
∴==2.
解法二:不妨设BF=2,CG=3,连接CE,则Rt△CA'E≌Rt△CDE,推出A'C=CD=AB=A'B',==1,推出GF=CG=3,BC=8,在Rt△CB'F,勾股得CB'=4 则A'B'=2,
故选:A.
19.解:∵=,
∴=,
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∴=,
∴=,
∴BC=15(cm),
故选:C.
20.解:在平行四边形ABCD中,AB∥DC,
∴∠AEF=∠CDF,∠EAF=∠DCF,
∴△AEF∽△CDF,
∴S△AEF:S△CDF=,
∵S△AEF:S△CDF=4:25,
∴=,
故选:A.
21.解:∵四边形ABCD、四边形BEFG是正方形,
∴AB=BC,BG=BE,∠ABC=90°=∠GBE,
∴∠ABC+∠CBG=∠GBE+∠CBG,即∠ABG=∠EBC,
∴△ABG≌△CBE(SAS),
∴∠BAG=∠BCE,
∵∠BAG+∠APB=90°,
∴∠BCE+∠APB=90°,
∴∠BCE+∠OPC=90°,
∴∠POC=90°,
∴EC⊥AG,故①正确;
取AC的中点K,如图:
在Rt△AOC中,K为斜边AC上的中点,
∴AK=CK=OK,
在Rt△ABC中,K为斜边AC上的中点,
∴AK=CK=BK,
∴AK=CK=OK=BK,
∴A、B、O、C四点共圆,
∴∠BOA=∠BCA,
∵∠BPO=∠CPA,
∴△OBP∽△CAP,故②正确,
∵∠AOC=∠ADC=90°,
∴∠AOC+∠ADC=180°,
∴A、O、C、D四点共圆,
∵AD=CD,
∴∠AOD=∠DOC=45°,故④正确,
由已知不能证明OB平分∠CBG,故③错误,
故正确的有:①②④,
故选:D.
22.解:∵四边形ABCD为平行四边形,
∴AD∥BC,AB∥CD,BC=AD,
∴△AEF∽△BCF,
∴=,
故A选项错误;
∵AD∥BC,
∴△DEG∽△BCG,
∴=,
故B选项正确;
∵AB∥CD,
∴△CDG∽△FBG,
∴=,
故C选项正确;
∵△AEF∽△BCF,
∴=,
∵BC=AD,
∴=,
故D选项正确;
故选:A.
选择题专题提升训练(附答案)
1.如图,在△ABC中,点D、E分别是线段AB、AC的中点,若S△ADE=2,则四边形BCED的面积是( )
A.4 B.6 C.8 D.10
2.如图,AB∥CD,AC,BD相交于点E,AE=1,EC=2,DE=3,则BD的长为( )
A. B.4 C. D.6
3.如图,菱形ABCD中,点E是边CD的中点,EF垂直AB交AB的延长线于点F,若BF:CE=1:2,EF=,则菱形ABCD的边长是( )
A.3 B.4 C.5 D.
4.如图,在Rt△ABC纸片中,∠ACB=90°,AC=4,BC=3,点D,E分别在BC、AB边上,连接DE,将△BDE沿DE翻折,使点B落在点F的位置,连接AF,若四边形BEFD是菱形,则AF的长的最小值为( )
A. B. C. D.
5.如图,在△ABC中,D,E分别是AB和AC上的点,DE∥BC,若=,那么=( )
A. B. C. D.
6.如图,D、E分别为△ABC的边AB、AC上的点,若∠1=∠B,=,△ADE的面积等于2,则△ABC的面积为( )
A.4 B.8 C.10 D.12
7.如图,在矩形ABCD中,E是BC边上一点,∠AED=90°,∠EAD=30°,F是AD边的中点,EF=4cm,则BE的长为( )
A.6cm B. C. D.8cm
8.如图,a∥b∥c∥d∥e,每相邻两条直线之间的距离均相等.点A,B,C分别在直线a,c,e上,AC交b于点D,BC交d于点G,AB分别交c,d于点E,F.若四边形DEFG的面积为4,则△ABC的面积为( )
A.8 B. C. D.12
9.如图,在△ABC中,点D,E分别在AB,AC上,若,且△ADE的面积为9,则四边形BCED的面积为( )
A.18 B.27 C.72 D.81
10.如图,在菱形ABCD中,AB=2,E为AB的中点,CE交BD于点F,且∠ADB=∠BCE,则BF的长为( )
A. B. C. D.
11.如图,在矩形ABCD中,AB<BC,连接AC,分别以点A,C为圆心,大于AC的长为半径画弧,两弧交于点M,N,直线MN分别交AD,BC于点E,F.下列结论:
①四边形AECF是菱形;
②∠AFB=2∠ACB;
③AC EF=CF CD;
④若AF平分∠BAC,则CF=2BF.
其中正确结论的个数是( )
A.4 B.3 C.2 D.1
12.如图,在正方形ABCD中,点G是BC上一点,且,连接DG交对角线AC于F点,过D点作DE⊥DG交CA的延长线于点E,若AE=3,则DF的长为( )
A.2 B. C. D.
13.如图,等腰△ABC的面积为2,AB=AC,BC=2.作AE∥BC且AE=BC.点P是线段AB上一动点,连结PE,过点E作PE的垂线交BC的延长线于点F,M是线段EF的中点.那么,当点P从A点运动到B点时,点M的运动路径长为( )
A. B.3 C.2 D.4
14.如图,在△ABC中,AB<AC,将△ABC以点A为中心逆时针旋转得到△ADE,点D在BC边上,DE交AC于点F.下列结论:①△AFE∽△DFC;②DA平分∠BDE;③∠CDF=∠BAD,其中所有正确结论的序号是( )
A.①② B.②③ C.①③ D.①②③
15.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=2:3,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A.2:3 B.2:5 C.4:25 D.4:9
16.如图,在△ABC中,D、E分别为线段BC、BA的中点,设△ABC的面积为S1,△EBD的面积为S2,则=( )
A. B. C. D.
17.如图,在 ABCD中,点E是边AD的中点,EC交对角线BD于点F,则BF:FD等于( )
A.3:2 B.3:1 C.1:1 D.2:1
18.如图是一张矩形纸片ABCD,点E为AD中点,点F在BC上,把该纸片沿EF折叠,点A,B的对应点分别为A′,B′,A′E与BC相交于点G,B′A′的延长线过点C.若=,则的值为( )
A.2 B. C. D.
19.如图,在△ABC中,点D、E分别在边AB、AC上,若DE∥BC,,DE=6cm,则BC的长为( )
A.9cm B.12cm C.15cm D.18cm
20.如图,在平行四边形ABCD中,E为AB上一点,连接AC、DE交于点F,S△AEF:S△CDF=4:25,则为( )
A.2:5 B.5:2 C.2:7 D.4:25
21.如图,正方形ABCD与正方形BEFG有公共顶点B,连接EC、GA,交于点O,GA与BC交于点P,连接OD、OB,则下列结论一定正确的是( )
①EC⊥AG;②△OBP∽△CAP;③OB平分∠CBG;④∠AOD=45°;
A.①③ B.①②③ C.②③ D.①②④
22.如图,在平行四边形ABCD中,点F在BA的延长线上,连接CF交AD于E,交BD于G,下列结论错误的是( )
A.= B.= C.= D.=
参考答案
1.解:∵点D、E分别是线段AB、AC的中点,
∴DE∥BC,DE:BC=1:2,
∴△ADE∽△ABC,
∵S△ADE=2,
∴S△ABC=2÷=8,
∴四边形BCED的面积是8﹣2=6,
故选:B.
2.解:∵AB∥CD,
∴△ABE∽△CDE,
∴=,即=,
∴BE=1.5,
∴BD=BE+DE=4.5.
故选:C.
3.解:过点D作DH⊥AB于点H,如图,
∵四边形ABCD是菱形,
∴AD=AB=CD,AB∥CD.
∵EF⊥AB,DH⊥AB,
∴DH∥EF,
∴四边形DHFE为平行四边形,
∴HF=DE,DH=EF=.
∵点E是边CD的中点,
∴DE=CD,
∴HF=CD=AB.
∵BF:CE=1:2,
∴设BF=x,则CE=2x,
∴CD=4x,DE=HF=2x,
AD=AB=4x,
∴AF=AB+BF=5x.
∴AH=AF﹣HF=3x.
在Rt△ADH中,
∵DH2+AH2=AD2,
∴.
解得:x=±1(负数不合题意,舍去),
∴x=1.
∴AB=4x=4.
即菱形ABCD的边长是4,
故选:B.
4.解:如图,连接BF交ED于点O,设EF与AC交于点G,
∵四边形BEFD是菱形,
∴BF平分∠ABC,
∴点F在∠ABC的平分线上运动,
∴当AF⊥BF时,AF的长最小.
在菱形BEFD中,BF⊥ED,OB=OF,EF∥BC,
∴EO∥AF,
∴△BEO∽△BAF,
∴===,
∴BE=AB=AE.
在Rt△ABC中,AC=4,BC=3,
∴AB=5,
∴BE=AE=2.5,
∵AF⊥BF.
∴EF=2.5,
∵EF∥BC,
∴△AGE∽△ACB,
∴===,∠AGE=∠ACB=90°,
∴EG=BC=1.5,AG=AC=2,
∴GF=EF﹣EG=1.
∵∠AGF=∠AGE=90°,
∴AF===.
故选:A.
5.解:∵DE∥BC,
∴△ADE∽△ABC,
∴=,
∵=,
∴=,
∴==.
故选:D.
6.解:∵∠1=∠B,∠A=∠A,
∴△ADE∽△ACB,
∵=,
∴=,
∵△ADE的面积等于2,
∴△ACB的面积等于8.
故选:B.
7.解:∵∠AED=90°,F是AD边的中点,
∴EF=AF=DF=AD=4,
∴AD=8,
∵∠AED=90°,∠EAD=30°,
∴DE=AD=4,
∴AE===4,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AEB=∠EAD=30°,
∵cos∠AEB=,
∴BE=AE cos30°=4×=6(cm),
故选:A.
8.解:由图象可得,点D,E,F,G分别为AC,AB,EB,BC的中点,
∴DG,DE,FG分别为△CAB,△ABC,△BEC的中位线,
∴S△CDG=S△AED=S△ABC,S△BFG=S△BEC=S△ABC,
∵四边形DEFG的面积为4,
∴S△ABC﹣S△CDG﹣S△AED﹣S△BFG=S△ABC=4,
∴S△ABC=.
故选:C.
9.解:∵,∠A=∠A,
∴△ADE∽△ABC,
∴=()2=()2=,
∵△ADE的面积为9,
∴△ABC的面积=81,
∴四边形BCED的面积=△ABC的面积﹣△ADE的面积
=81﹣9
=72,
故选:C.
10.解:∵四边形ABCD是菱形,
∴AD=AB=CD=BC=2,AB∥CD,AD∥BC,
∴∠ADB=∠FBC,
∵∠ADB=∠BCE,
∴∠FBC=∠FCB,
∴FB=FC,
∵E为AB的中点,
∴BE=AB=1,
∵AB∥CD,
∴∠ABF=∠DCE,∠BEF=∠DCE,
∴△BEF∽△DCF,
∴=,
∴FC=2EF,
∴FB=2EF,
设EF=x,则BF=FC=2x,
∴EC=EF+CF=3x,
∵AB=AD,
∴∠ADB=∠ABD,
∴∠ABD=∠BCE,
∵∠BEF=∠BEF,
∴△BEF∽△CEB,
∴,
∴BE2=EF EC,
∴12=x 3x,
∴或x=﹣(舍去),
∴BF=2x=,
故选:B.
11.解:根据题意知,BF垂直平分AC,
在△AOE和△COF中,
,
∴△AOE≌△COF(AAS),
∴OE=OF,
∴AE=AF=CF=CE,
即四边形AECF是菱形,
故①结论正确;
∵∠AFB=∠FAO+∠ACB,AF=FC,
∴∠FAO=∠ACB,
∴∠AFB=2∠ACB,
故②结论正确;
∵S四边形AECF=CF CD=AC OE×2=AC EF,
故③结论不正确;
若AF平分∠BAC,则∠BAF=∠FAC=∠CAD=90°=30°,
∴AF=2BF,
∵CF=AF,
∴CF=2BF,
故④结论正确;
故选:B.
12.解:过点E作EH⊥AD,交DA延长线于H,
∴∠H=90°,
在正方形ABCD中,AB=BC=CD=AD,∠BAD=∠B=∠BCD=∠ADC=90°,
∴∠2+∠3=90°,∠H=∠BCD,
∵DE⊥DG,
∴∠EDG=90°,
∴∠2+∠1=90°,
∴∠1=∠3,
∴△DEH∽△DGC,
∴=,
∵,
∴设GC=x,则BG=2x,DC=BC=3x,
∴=,
∴DH=3EH,
∵AC是正方形ABCD对角线,
∴∠DAC=45°,
∵∠EAH=∠DAC=45°,
∴∠HEA=45°,
∴EH=HA,
∴EH2+HA2=9,
∴EH=HA=,
∴DH=,
∴AD=3,
∴GC=,
∴DG==2,
∵在正方形ABCD中,AD∥BC,
∴==,
∴DF=3GF,
∴DF=;
故选:D.
13.解:如图,过点A作AH⊥BC于点H.
当点P与A重合时,点F与C重合,当点P与B重合时,点F的对应点为F″,
点M的运动轨迹是△ECF″的中位线,M′M″=CF″,
∵AB=AC,AH⊥BC,
∴BH=CH,
∵AE∥BC,AE=BC,
∴AE=CH,
∴四边形AHCE是平行四边形,
∵∠AHC=90°,
∴四边形AHCE是矩形,
∴EC⊥BF″,AH=EC,
∵BC=2,S△ABC=2,
∴×2×AH=2,
∴AH=EC=2,
∵∠BEF″=∠ECB=∠ECF″,
∴∠BEC+∠CEF″=90°,
∠CEF″+∠F″=90°,
∴∠BEC=∠F″,
∴△ECB∽△F″CE,
∴EC2=CB CF″,
∴CF″==6,
∴M′M″=3
故选:B.
14.解:∵将△ABC以点A为中心逆时针旋转得到△ADE,
∴∠BAC=∠DAE,∠B=∠ADE,AB=AD,∠E=∠C,
∴∠B=∠ADB,
∴∠ADE=∠ADB,
∴DA平分∠BDE,
∴②符合题意;
∵∠AFE=∠DFC,∠E=∠C,
∴△AFE∽△DFC,
∴①符合题意;
∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠FAE,
∵△AFE∽△DFC,
∴∠FAE=∠CDF,
∴∠BAD=∠CDF,
∴③符合题意;
故选:D.
15.解:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴△DEF∽△BAF,
∵DE:EC=2:3,
∴DE:DC=2:5,
∴DE:AB=2:5,
∴S△DEF:S△BAF=()2=,
故选:C.
16.解:在△ABC中,D、E分别为线段BC、BA的中点,
∴DE为△ABC的中位线,
∴DE∥AC,DE=AC,
∴△BED∽△BAC,
∵=,
∴=,
即=,
故选:B.
17.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△DEF∽△BCF,
∴BF:FD=BC:DE,
又∵点E是边AD的中点,
∴DE=AD=BC,
∴BF:FD=BC:DE=2:1,
故选:D.
18.解:连接FG,CA′,过点G作GT⊥AD于点T.设AB=x,AD=y.
∵=,
∴可以假设BF=2k,CG=3k.
∵AE=DE=y,
由翻折的性质可知EA=EA′=y,BF=FB′=2k,∠AEF=∠GEF,
∵AD∥CB,
∴∠AEF=∠EFG,
∴∠GEF=∠GFE,
∴EG=FG=y﹣5k,
∴GA′=y﹣(y﹣5k)=5k﹣y,
∵C,A′,B′共线,GA′∥FB′,
∴=,
∴=,
∴y2﹣12ky+32k2=0,
∴y=8k或y=4k(舍去),
∴AE=DE=4k,
∵四边形CDTG是矩形,
∴CG=DT=3k,
∴ET=k,
∵EG=8k﹣5k=3k,
∴AB=CD=GT==2k,
∴==2.
解法二:不妨设BF=2,CG=3,连接CE,则Rt△CA'E≌Rt△CDE,推出A'C=CD=AB=A'B',==1,推出GF=CG=3,BC=8,在Rt△CB'F,勾股得CB'=4 则A'B'=2,
故选:A.
19.解:∵=,
∴=,
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∴=,
∴=,
∴BC=15(cm),
故选:C.
20.解:在平行四边形ABCD中,AB∥DC,
∴∠AEF=∠CDF,∠EAF=∠DCF,
∴△AEF∽△CDF,
∴S△AEF:S△CDF=,
∵S△AEF:S△CDF=4:25,
∴=,
故选:A.
21.解:∵四边形ABCD、四边形BEFG是正方形,
∴AB=BC,BG=BE,∠ABC=90°=∠GBE,
∴∠ABC+∠CBG=∠GBE+∠CBG,即∠ABG=∠EBC,
∴△ABG≌△CBE(SAS),
∴∠BAG=∠BCE,
∵∠BAG+∠APB=90°,
∴∠BCE+∠APB=90°,
∴∠BCE+∠OPC=90°,
∴∠POC=90°,
∴EC⊥AG,故①正确;
取AC的中点K,如图:
在Rt△AOC中,K为斜边AC上的中点,
∴AK=CK=OK,
在Rt△ABC中,K为斜边AC上的中点,
∴AK=CK=BK,
∴AK=CK=OK=BK,
∴A、B、O、C四点共圆,
∴∠BOA=∠BCA,
∵∠BPO=∠CPA,
∴△OBP∽△CAP,故②正确,
∵∠AOC=∠ADC=90°,
∴∠AOC+∠ADC=180°,
∴A、O、C、D四点共圆,
∵AD=CD,
∴∠AOD=∠DOC=45°,故④正确,
由已知不能证明OB平分∠CBG,故③错误,
故正确的有:①②④,
故选:D.
22.解:∵四边形ABCD为平行四边形,
∴AD∥BC,AB∥CD,BC=AD,
∴△AEF∽△BCF,
∴=,
故A选项错误;
∵AD∥BC,
∴△DEG∽△BCG,
∴=,
故B选项正确;
∵AB∥CD,
∴△CDG∽△FBG,
∴=,
故C选项正确;
∵△AEF∽△BCF,
∴=,
∵BC=AD,
∴=,
故D选项正确;
故选:A.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
