人教版七年级上册4.3.2角的比较课件(共20张PPT)
文档属性
| 名称 | 人教版七年级上册4.3.2角的比较课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 819.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-16 10:02:09 | ||
图片预览






文档简介
(共20张PPT)
§4.3.2 角的比较和运算(2)
复习回顾
1.什么叫线段的中点?
如果线段上一点将线段分成了相等的
两条线段,那么这个点叫线段的中点。
2.如何作出线段的中点?
(2)折叠法
(1)度量法
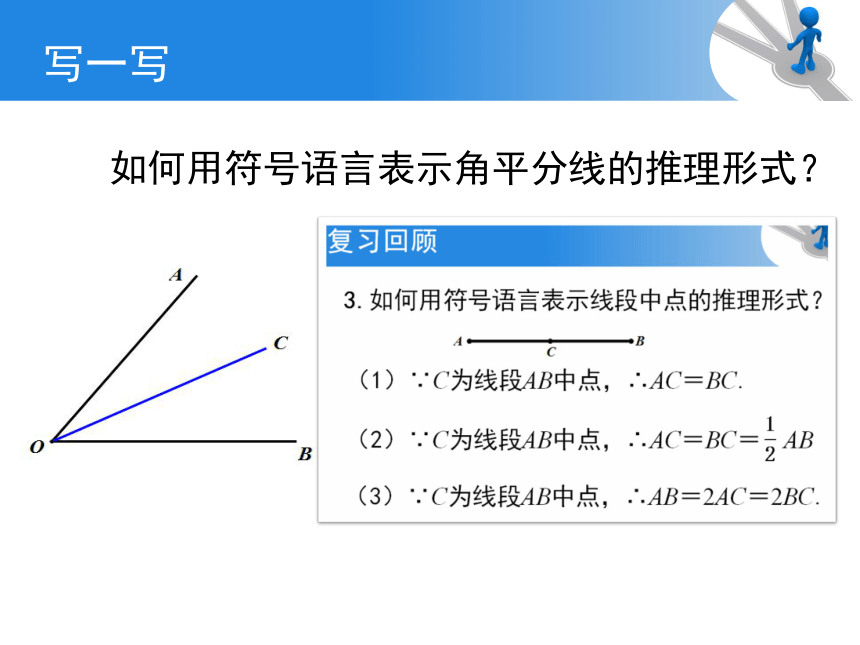
3.如何用符号语言表示线段中点的推理形式?
(1)∵C为线段AB中点,∴AC=BC.
(2)∵C为线段AB中点,∴AC=BC= AB
(3)∵C为线段AB中点,∴AB=2AC=2BC.
复习回顾
如何将一个角平均分成相等的两个角?
试一试
请你任意画一个角∠AOB,
并把∠AOB平均分成相等的两个角.
画一画
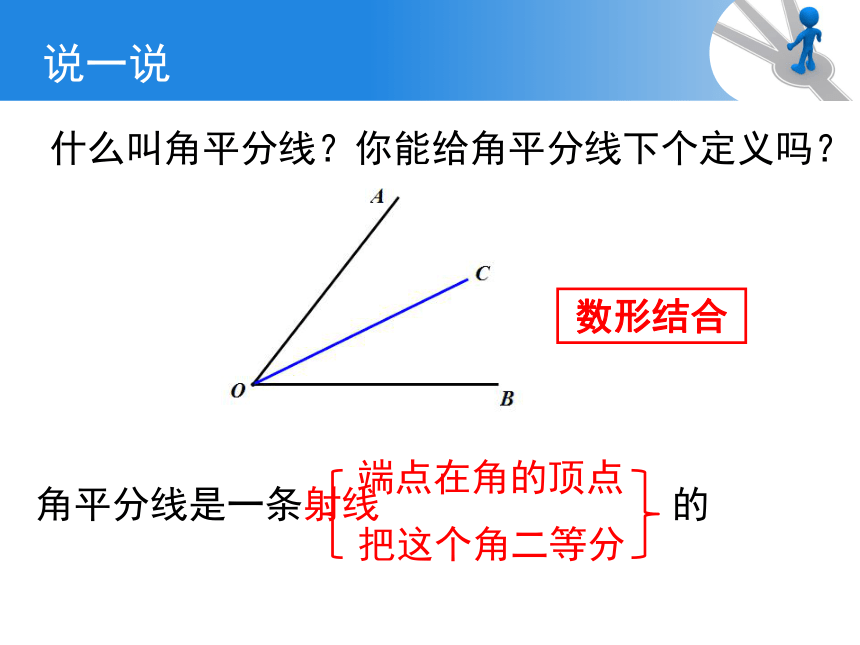
什么叫角平分线?你能给角平分线下个定义吗?
说一说
端点在角的顶点
把这个角二等分
射线
角平分线是一条
的
数形结合
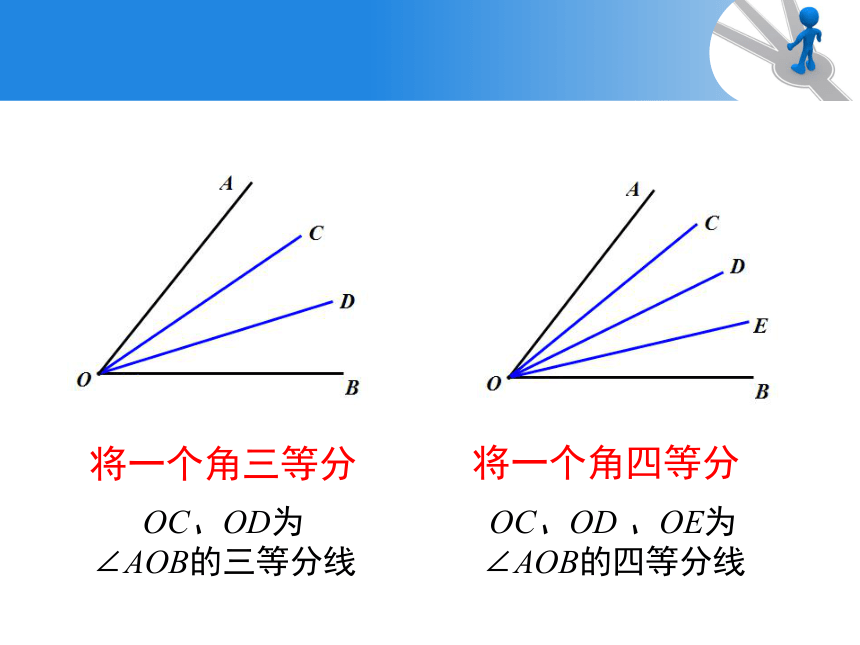
将一个角三等分
OC、OD为
∠AOB的三等分线
将一个角四等分
OC、OD 、OE为
∠AOB的四等分线
如何用符号语言表示角平分线的推理形式?
写一写
想一想
回顾角平分线图形、定义和推理形式得出的过程,你觉得困难吗?为什么?
猜想
实验
观察
发现
归纳
我们的探索之旅
应用
归纳
角平分线
数学定义
推理形式
线段中点
数学定义
推理形式
类比
图形
文字
符号
线段相等倍分关系
角的相等倍分关系
数形结合
如图,OC是∠AOB的平分线,
(1)若∠AOC=60°,则∠BOC= .
例1
60°
(2)若∠AOB=120°,则∠AOC= .
(3)若∠BOC=60°,则∠AOB= .
60°
120°
根据已知条件和所求,
合理选择角平分线的
三种不同推理形式.
如图,∠AOB=140°,OC是∠AOB的平分线,
OD是∠AOC的平分线,求∠BOD的度数.
例2
不易直接求得的角
易求的两角和或差
角平分线
已知条件
(2) 若∠AOB=160°,
则∠DOE= .
如图,OC是∠AOB的平分线,OD是
∠AOC的平分线,OE是∠BOC的平分线,
(1) 若∠AOB=140°,则∠DOE= .
70°
80°
例3
你有什么发现吗?
∠DOE = ∠AOB
合作探究
如图,OC是∠AOB内部任意一条射线,
OD是∠AOC的平分线,
OE是∠BOC的平分线,
则∠DOE与∠AOB有何数量关系?
试证明你的结论。
合作探究
如图, OC是∠AOB外部一条射线,
OD是∠AOC的平分线,
OE是∠BOC的平分线,
∠DOE与∠AOB还有以上数量关系吗?
回顾反思
本节课学习了哪些知识?
是运用了什么方法学习的?
你都有什么收获?
应用
角平分线
数学定义
推理形式
类比
图形
文字
符号
角的相等倍分关系
线
段
中
点
数形结合
三种推理形式的灵活选择
将一角转化为两角和或差
将问题由特殊推广到一般
回顾反思
猜想
实验
观察
发现
归纳
我们的探索之旅
回顾反思
1. 课本习题4.3第5,9题.
作业
2. 拓展:如图,OC是∠AOB外部一条射线,OD是∠AOC的平分线,OE是∠BOC的平分线,请依题意补全图形,并试说明∠DOE与∠AOB有何数量关系?
§4.3.2 角的比较和运算(2)
复习回顾
1.什么叫线段的中点?
如果线段上一点将线段分成了相等的
两条线段,那么这个点叫线段的中点。
2.如何作出线段的中点?
(2)折叠法
(1)度量法
3.如何用符号语言表示线段中点的推理形式?
(1)∵C为线段AB中点,∴AC=BC.
(2)∵C为线段AB中点,∴AC=BC= AB
(3)∵C为线段AB中点,∴AB=2AC=2BC.
复习回顾
如何将一个角平均分成相等的两个角?
试一试
请你任意画一个角∠AOB,
并把∠AOB平均分成相等的两个角.
画一画
什么叫角平分线?你能给角平分线下个定义吗?
说一说
端点在角的顶点
把这个角二等分
射线
角平分线是一条
的
数形结合
将一个角三等分
OC、OD为
∠AOB的三等分线
将一个角四等分
OC、OD 、OE为
∠AOB的四等分线
如何用符号语言表示角平分线的推理形式?
写一写
想一想
回顾角平分线图形、定义和推理形式得出的过程,你觉得困难吗?为什么?
猜想
实验
观察
发现
归纳
我们的探索之旅
应用
归纳
角平分线
数学定义
推理形式
线段中点
数学定义
推理形式
类比
图形
文字
符号
线段相等倍分关系
角的相等倍分关系
数形结合
如图,OC是∠AOB的平分线,
(1)若∠AOC=60°,则∠BOC= .
例1
60°
(2)若∠AOB=120°,则∠AOC= .
(3)若∠BOC=60°,则∠AOB= .
60°
120°
根据已知条件和所求,
合理选择角平分线的
三种不同推理形式.
如图,∠AOB=140°,OC是∠AOB的平分线,
OD是∠AOC的平分线,求∠BOD的度数.
例2
不易直接求得的角
易求的两角和或差
角平分线
已知条件
(2) 若∠AOB=160°,
则∠DOE= .
如图,OC是∠AOB的平分线,OD是
∠AOC的平分线,OE是∠BOC的平分线,
(1) 若∠AOB=140°,则∠DOE= .
70°
80°
例3
你有什么发现吗?
∠DOE = ∠AOB
合作探究
如图,OC是∠AOB内部任意一条射线,
OD是∠AOC的平分线,
OE是∠BOC的平分线,
则∠DOE与∠AOB有何数量关系?
试证明你的结论。
合作探究
如图, OC是∠AOB外部一条射线,
OD是∠AOC的平分线,
OE是∠BOC的平分线,
∠DOE与∠AOB还有以上数量关系吗?
回顾反思
本节课学习了哪些知识?
是运用了什么方法学习的?
你都有什么收获?
应用
角平分线
数学定义
推理形式
类比
图形
文字
符号
角的相等倍分关系
线
段
中
点
数形结合
三种推理形式的灵活选择
将一角转化为两角和或差
将问题由特殊推广到一般
回顾反思
猜想
实验
观察
发现
归纳
我们的探索之旅
回顾反思
1. 课本习题4.3第5,9题.
作业
2. 拓展:如图,OC是∠AOB外部一条射线,OD是∠AOC的平分线,OE是∠BOC的平分线,请依题意补全图形,并试说明∠DOE与∠AOB有何数量关系?
