人教版七年级上册4.1.2点、线、面、体-课件(共23张PPT)
文档属性
| 名称 | 人教版七年级上册4.1.2点、线、面、体-课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-16 10:43:44 | ||
图片预览





文档简介
(共23张PPT)
直线、射线、线段(一)
问题1:小学的时候我们已经学习过直线、射线和线段,请同学们回忆一下他们的形状并分别画出一条直线、射线和线段.
●
●
●
直线
射线
线段
·O
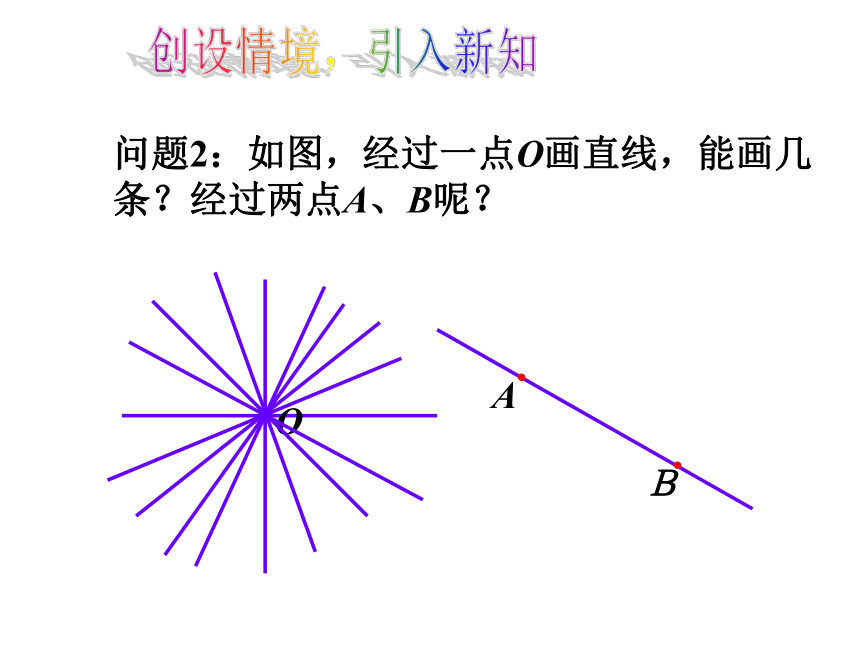
问题2:如图,经过一点O画直线,能画几条?经过两点A、B呢?
A
·
B
·
经过思考与画图,我们可以得到一个基本的事实:
经过两点有一条直线,并且只有一条直线.
简单说成:两点确定一条直线.
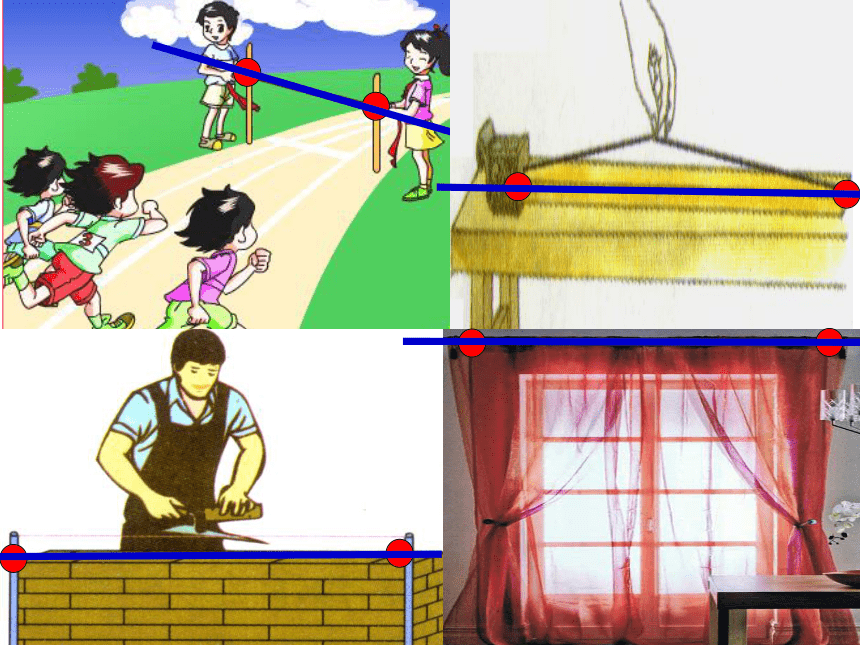
问题3:你还能举出一些实际生活中应用“两点确定一条直线”的实例吗?
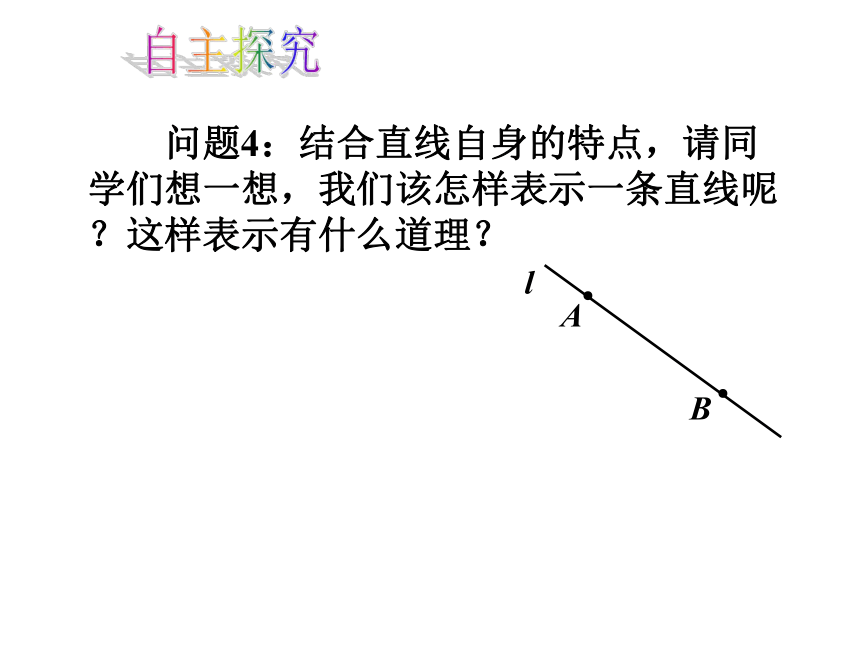
问题4:结合直线自身的特点,请同学们想一想,我们该怎样表示一条直线呢?这样表示有什么道理?
●
●
A
B
l
B
A
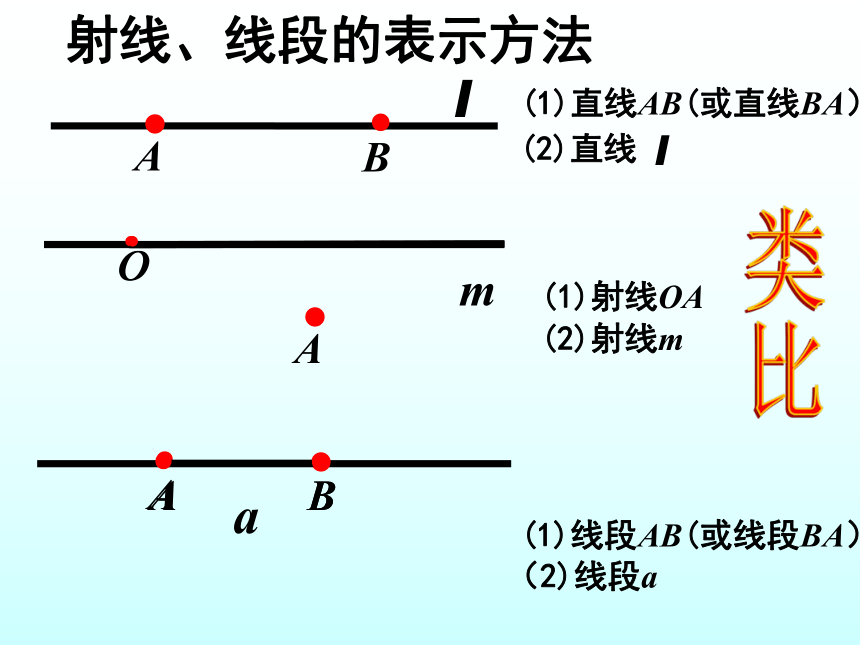
射线、线段的表示方法
ι
(2)直线
ι
(1)射线OA
m
(2)射线m
B
A
●
A
●
●
B
a
(1)线段AB(或线段BA)
(2)线段a
(1)直线AB(或直线BA)
O
O
A
基础达标之眼疾手快
1.选择题:
(2)下列各直线的表示方法中,正确的是( )
A.直线A B.直线AB
C.直线ab D.直线Ab
B
基础达标之眼疾手快
1.选择题:
(1)下列说法正确的是( )
A.直线AB和直线BA是两条直线
B.射线AB和射线BA是两条射线
C.线段AB和线段BA不是同一条线段
D.直线AB和直线a不能是同一条直线
B
直线、射线、线段的区别与联系
名称 图形 表示方法 延伸方向 端点个数 能否度量
A
B
ι
A
O
m
A
B
a
射线
直线
线段
你能由线段得到射线和直线吗?
问题5:当点与直线、直线与直线同时在一个图形中出现的时候,我们应怎样描述它们之间的关系呢?如图试着描述图中点与直线、直线与直线的关系.
●
●
P
O
l
●
O
a
b
问题6:
(1)用恰当的语句描述图中点与直线,直线与直线的关系.
P
·
·
Q
l
A
·
A
a
b
c
B
C
(2)按下列语句画出图形:
①直线EF经过点C;
②点A在直线 l 外;
③直线AB与直线CD相交于点A.
E
·
·
F
C
·
①
l
A
·
②
③
D
·
·
C
A
B
·
·
基础达标之眼疾手快
归纳:
(1)点与直线的位置关系:
点在直线上(直线经过点);
点不在直线上(直线不经过点).
(2)当两条不同的直线有一个公共点时,我们就称这两条直线相交,这个公共点叫做他们的交点.
(3)直线、射线、线段的表示.
练习1:
(1)判断下列说法是否正确:
①线段AB与射线AB都是直线AB的一部分;
②直线AB与直线BA是同一条直线;
③射线AB和射线BA是同一条射线;
④把线段向一个方向无限延伸可得到射线,把线段向两个方向无限延伸可得到直线.
基础达标之眼疾手快
1.选择题:
(3)下列写法中正确的是( )
A.直线a,b相交于点n
B.直线AB,CD相交于点m
C.直线ab,cd相交于点M
D.直线AB,CD相交于点M
D
基础达标之眼疾手快
1.选择题:
(4)下列用几何语言叙述图形的含义正确的有( )
A.1个 B.2个 C.3个 D.4个
●
A
m
点A在直线m外
●
O
n
直线n经点O
O
a
b
直线a与直线b相交于点O
●
●
●
A B C
ι
点A、B、C在直线ι上
D
基础达标之眼疾手快
2、按下列语句画出图形:
(1)直线MN经过点A;
(2)点O在直线ι外;
(3)经过点O的三条线段a、b、c;
(4)线段AB、CD相交于点P。
3、(1)如图,共有几条射线、几条线段?
4 1
6 3
(2)如图,共有几条射线、几条线段?
(3)如图,共有几条射线、几条线段?
●
●
A
●
●
A B C
●
●
2 0
能力提升之规律探究
A B
4、(1)平面内过A、B、C三点中的任意两点作直线,小明说有一条;小刚说有三条;小丽说不是一条就是三条;你赞同谁的观点?为什么?
(2)A、B、C、D为同一平面内的四点由这四点可以确定几条直线?
能力提升之拓展延伸
练习2:(2)按下列语句画出图形:
①点A在线段MN上; ③经过O点的三条线段a,b,c;
②射线AB不经过点P;④线段AB、CD相交于点B.
M
N
A
a
b
c
O
●
P
B
A
A
B
C
D
直线、射线、线段(一)
问题1:小学的时候我们已经学习过直线、射线和线段,请同学们回忆一下他们的形状并分别画出一条直线、射线和线段.
●
●
●
直线
射线
线段
·O
问题2:如图,经过一点O画直线,能画几条?经过两点A、B呢?
A
·
B
·
经过思考与画图,我们可以得到一个基本的事实:
经过两点有一条直线,并且只有一条直线.
简单说成:两点确定一条直线.
问题3:你还能举出一些实际生活中应用“两点确定一条直线”的实例吗?
问题4:结合直线自身的特点,请同学们想一想,我们该怎样表示一条直线呢?这样表示有什么道理?
●
●
A
B
l
B
A
射线、线段的表示方法
ι
(2)直线
ι
(1)射线OA
m
(2)射线m
B
A
●
A
●
●
B
a
(1)线段AB(或线段BA)
(2)线段a
(1)直线AB(或直线BA)
O
O
A
基础达标之眼疾手快
1.选择题:
(2)下列各直线的表示方法中,正确的是( )
A.直线A B.直线AB
C.直线ab D.直线Ab
B
基础达标之眼疾手快
1.选择题:
(1)下列说法正确的是( )
A.直线AB和直线BA是两条直线
B.射线AB和射线BA是两条射线
C.线段AB和线段BA不是同一条线段
D.直线AB和直线a不能是同一条直线
B
直线、射线、线段的区别与联系
名称 图形 表示方法 延伸方向 端点个数 能否度量
A
B
ι
A
O
m
A
B
a
射线
直线
线段
你能由线段得到射线和直线吗?
问题5:当点与直线、直线与直线同时在一个图形中出现的时候,我们应怎样描述它们之间的关系呢?如图试着描述图中点与直线、直线与直线的关系.
●
●
P
O
l
●
O
a
b
问题6:
(1)用恰当的语句描述图中点与直线,直线与直线的关系.
P
·
·
Q
l
A
·
A
a
b
c
B
C
(2)按下列语句画出图形:
①直线EF经过点C;
②点A在直线 l 外;
③直线AB与直线CD相交于点A.
E
·
·
F
C
·
①
l
A
·
②
③
D
·
·
C
A
B
·
·
基础达标之眼疾手快
归纳:
(1)点与直线的位置关系:
点在直线上(直线经过点);
点不在直线上(直线不经过点).
(2)当两条不同的直线有一个公共点时,我们就称这两条直线相交,这个公共点叫做他们的交点.
(3)直线、射线、线段的表示.
练习1:
(1)判断下列说法是否正确:
①线段AB与射线AB都是直线AB的一部分;
②直线AB与直线BA是同一条直线;
③射线AB和射线BA是同一条射线;
④把线段向一个方向无限延伸可得到射线,把线段向两个方向无限延伸可得到直线.
基础达标之眼疾手快
1.选择题:
(3)下列写法中正确的是( )
A.直线a,b相交于点n
B.直线AB,CD相交于点m
C.直线ab,cd相交于点M
D.直线AB,CD相交于点M
D
基础达标之眼疾手快
1.选择题:
(4)下列用几何语言叙述图形的含义正确的有( )
A.1个 B.2个 C.3个 D.4个
●
A
m
点A在直线m外
●
O
n
直线n经点O
O
a
b
直线a与直线b相交于点O
●
●
●
A B C
ι
点A、B、C在直线ι上
D
基础达标之眼疾手快
2、按下列语句画出图形:
(1)直线MN经过点A;
(2)点O在直线ι外;
(3)经过点O的三条线段a、b、c;
(4)线段AB、CD相交于点P。
3、(1)如图,共有几条射线、几条线段?
4 1
6 3
(2)如图,共有几条射线、几条线段?
(3)如图,共有几条射线、几条线段?
●
●
A
●
●
A B C
●
●
2 0
能力提升之规律探究
A B
4、(1)平面内过A、B、C三点中的任意两点作直线,小明说有一条;小刚说有三条;小丽说不是一条就是三条;你赞同谁的观点?为什么?
(2)A、B、C、D为同一平面内的四点由这四点可以确定几条直线?
能力提升之拓展延伸
练习2:(2)按下列语句画出图形:
①点A在线段MN上; ③经过O点的三条线段a,b,c;
②射线AB不经过点P;④线段AB、CD相交于点B.
M
N
A
a
b
c
O
●
P
B
A
A
B
C
D
