数学人教A版(2019)必修第一册4.4.2 对数函数的图像和性质(共24张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.4.2 对数函数的图像和性质(共24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-13 19:35:10 | ||
图片预览



文档简介
(共24张PPT)
对数函数的图象和性质
新课程标准 核心素养
1.掌握对数函数的图象和性质; 数学抽象
2.通过观察图象,分析、归纳、总结对数函数的性质; 逻辑推理
3.利用对数函数的性质比较两个函数值的大小及解对数不等式; 数据分析
4.通过由抽象到具体,由具体到一般的数形结合思想总结对数函数性质. 数学建模
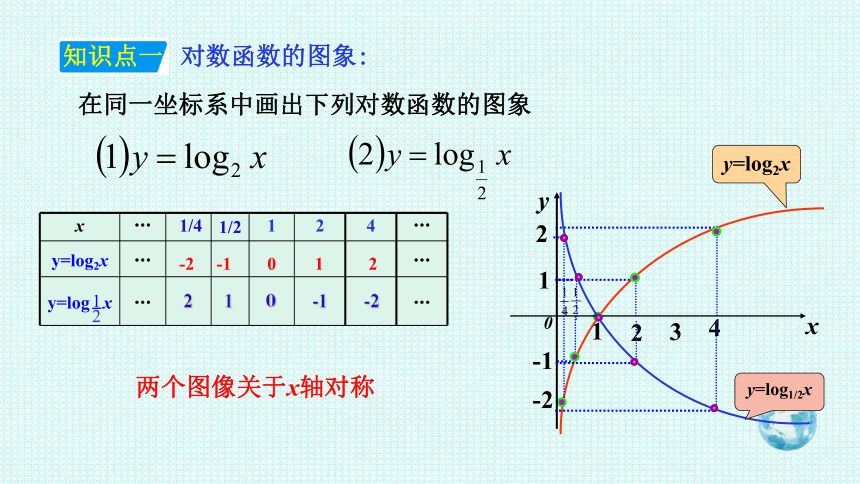
对数函数的图象:
知识点一
在同一坐标系中画出下列对数函数的图象
x … 1/4 1/2 1 2 4 …
y=log2x … …
y=log x … …
1
2
-2 -1 0 1 2
2 1 0 -1 -2
2
1
-1
-2
1
2
4
0
y
x
3
y=log2x
y=log1/2x
两个图像关于x轴对称
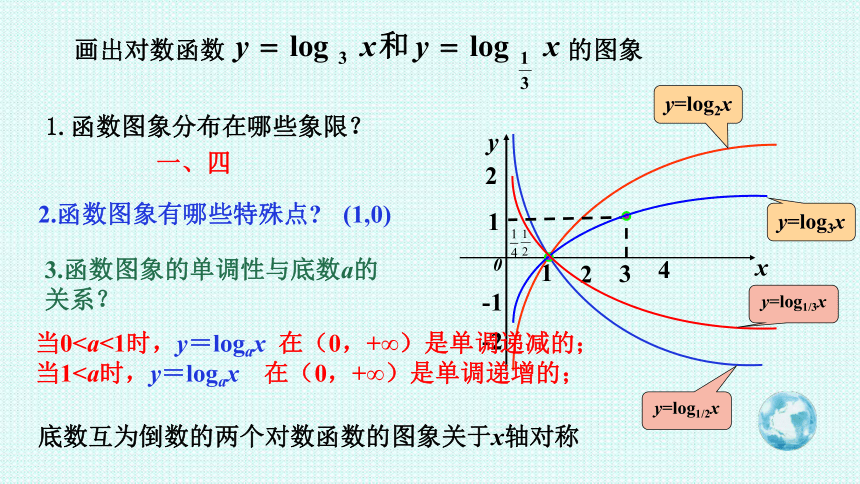
画出对数函数 的图象
2
1
-1
-2
1
2
4
0
y
x
3
y=log2x
y=log1/2x
y=log3x
y=log1/3x
1.函数图象分布在哪些象限?
一、四
2.函数图象有哪些特殊点
(1,0)
3.函数图象的单调性与底数a的关系?
当0当1底数互为倒数的两个对数函数的图象关于x轴对称
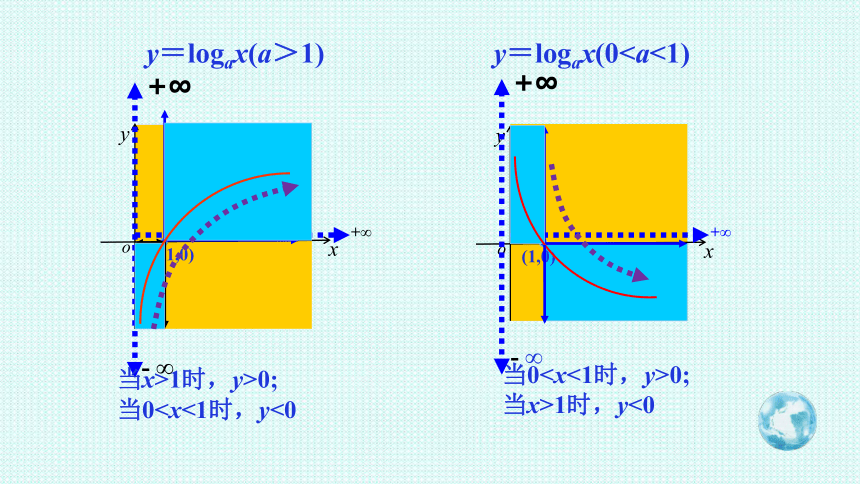
y=logax(a>1)
y=logax(0o
x
y
o
x
y
+∞
+∞
+∞
- ∞
+∞
- ∞
·
·
(1,0)
(1,0)
当x>1时,y>0;
当0当00;
当x>1时,y<0
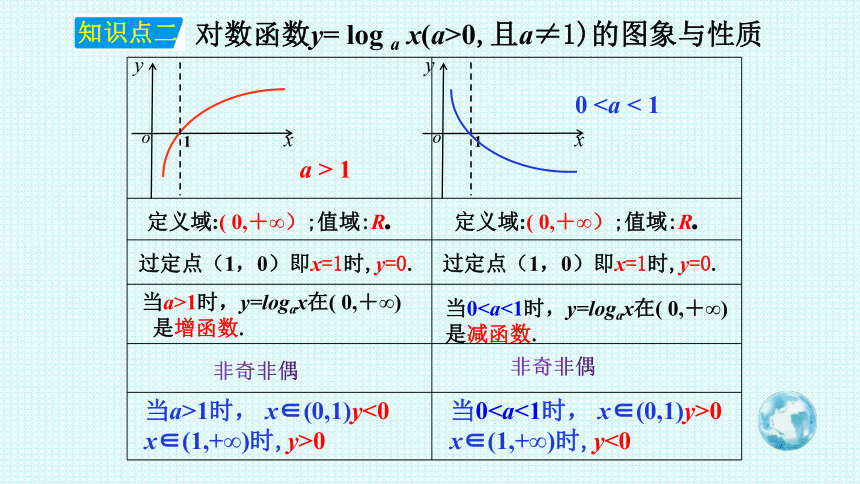
对数函数y= log a x(a>0,且a≠1)的图象与性质
o
x
y
1
o
x
y
1
定义域:( 0,+∞);值域:R.
定义域:( 0,+∞);值域:R.
过定点(1,0)即x=1时,y=0.
过定点(1,0)即x=1时,y=0.
当a>1时, x∈(0,1)y<0
x∈(1,+∞)时,y>0
当00
x∈(1,+∞)时,y<0
当a>1时,y=logax在( 0,+∞)
是增函数.
当0非奇非偶
非奇非偶
知识点二
a > 1
0 类型1 对数函数图像
角度一 对数型函数过定点问题
令对数型部分的真数为1,求出的x值为点的横坐标,
此时的函数值为点的纵坐标。
角度二 对数型函数图象的特征
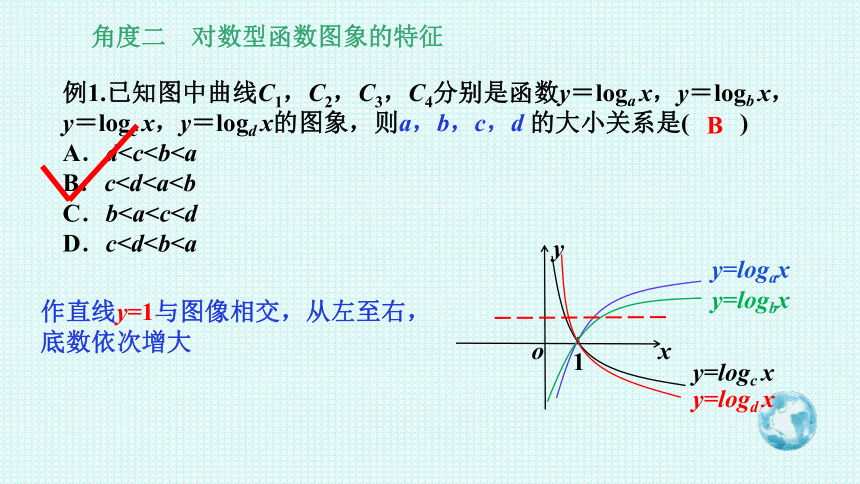
例1.已知图中曲线C1,C2,C3,C4分别是函数y=loga x,y=logb x,y=logc x,y=logd x的图象,则a,b,c,d 的大小关系是( )
A.dB.cC.bD.cx
y
o
1
y=logax
y=logbx
y=logc x
y=logd x
B
作直线y=1与图像相交,从左至右,
底数依次增大
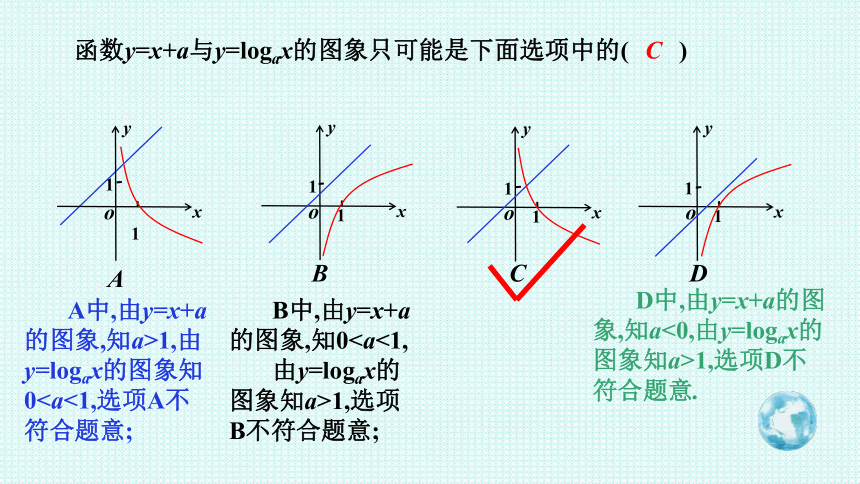
函数y=x+a与y=logax的图象只可能是下面选项中的( )
x
y
o
1
x
y
o
1
x
y
o
1
C
A
B
D
1
1
1
x
y
o
1
1
A中,由y=x+a的图象,知a>1,由y=logax的图象知0B中,由y=x+a的图象,知0由y=logax的图象知a>1,选项B不符合题意;
D中,由y=x+a的图象,知a<0,由y=logax的图象知a>1,选项D不符合题意.
C
角度三 作对数型函数的图象
作出函数y=|lg(x-1)|的图象
先画出函数y=lg x的图象
x
y
o
1
1
再将该函数图象向右平移1个单位长度
得到函数y=lg(x-1)的图象
最后把y=lg(x-1)的图象在x轴下方的部分
对称翻折到x轴上方
类型2 对数函数的性质
1.比较大小
例2.比较下列各组中两个值的大小:
(1) log25.3 , log24.7 (2) log0.27 , logo.29
(3) log3π , logπ3
(4) loga3.1 , loga5.2(a>0,a≠1)
y=log2x在( 0,+∞) 是增
函数.log25.3 > log24.7
y=log0.2x在( 0,+∞) 是减
函数.log0.27 > logo.29
log3π>1,0logπ3
当0 loga5.2;当a>1时,loga3.1< loga5.2
比较两个对数式的大小,一般有三种方法:
(1)若是同底的对数,则可直接利用对数函数的单调性,只需比较两个真数的大小即可.
(2) 同真的利用对数函数的图象或用换底公式转化.
(3) 底数和真数都不同,找中间量.
若底数为同一参数,则根据底数对对数函数单调性的影响,
对底数进行分类讨论.
log23与log54
2.解含对数型不等式
例3. (1)解不等式log5(1-x)>log5(3x-2).
1-x>0
3x-2>0
1-x>3x-2
x<1
x>
2
3
x<
3
4
{x| <x< }
2
3
3
4
1
2
(4).解不等式:loga(x-4)>loga(x-2).
x-4>0
x-2>0
x-4>x-2
x-4>0
x-2>0
x-4解集为(4,+∞)
3.对数型函数的奇偶性和单调性
[解析] 由题意,得x2-3x-10>0,∴(x-5)(x+2)>0,∴x<-2或x>5.
令u=x2-3x-10,
函数f(x)的单调递增区间即为函数u=x2-3x-10在定义域上的
单调递减区间.
y=log u
1
2
例5.已知函数f(x)=loga(x+1)-loga(1-x)(a>0且a≠1).
(1)求f(x)的定义域;
(2)判断函数f(x)的奇偶性并加以证明.
(2)由(1)知函数f(x)的定义域为(-1,1)关于原点对称.
∴f(-x)=loga(-x+1)-loga(1+x)
=-[loga(1+x)-loga(1-x)]=-f(x),
∴函数f(x)为奇函数
若函数y=loga(2-ax)在x∈[0,1]上是减函数,则a的取值范围是( )
A.(0,1) B.(1,2)
C.(0,2) D.(1,+∞)
令u=2-ax,由于a>0且a≠1,所以u=2-ax为减函数,
又根据对数函数定义域要求u=2-ax在[0,1]
上恒大于零,当x∈[0,1]时,umin=2-a>0,解得a<2.
根据复合函数单调性“同增异减”法则,要使f(x)=loga(2-ax)
在[0,1]上为减函数,则需y=logau为增函数,所以a>1.
综上可得1B
4.对数型函数的值域
[解析] (1)y=log2(x2+4)的定义域为R.∵x2+4≥4,
∴log2(x2+4)≥log24=2.
∴y=log2(x2+4)的值域为{y|y≥2}.
(2)设u=3+2x-x2,则u=-(x-1)2+4≤4.∵u>0,∴0函数f(x)=log2(3x+1)的值域为( )
A.(0,+∞) B.[0,+∞)
C.(1,+∞) D.[1,+∞)
[解析] ∵3x+1>1,且f(x)在(1,+∞)上单调递增,
∴log2(3x+1)>log21=0,故该函数的值域为(0,+∞).
( )
( )
( )
知识点三
反函数
指数函数y=ax与对数函数y=logax(a>0,且a≠1)互为__________,
它们定义域与值域正好________.
反函数
互换
互为反函数的两个函数的单调性相同,但单调区间不一定相同.
互为反函数的两个函数的图象关于直线y=x对称.
例8:作出 y=log2x , y=log x , y=lgx的图象.
1
1
x
y
o
log
1
3
指数函数y=ax的反函数是对数函数y=logax.
∵对数函数y=logax的图象过点(9,2).
∴2=loga9,解得a=3.
对数函数的图象和性质
新课程标准 核心素养
1.掌握对数函数的图象和性质; 数学抽象
2.通过观察图象,分析、归纳、总结对数函数的性质; 逻辑推理
3.利用对数函数的性质比较两个函数值的大小及解对数不等式; 数据分析
4.通过由抽象到具体,由具体到一般的数形结合思想总结对数函数性质. 数学建模
对数函数的图象:
知识点一
在同一坐标系中画出下列对数函数的图象
x … 1/4 1/2 1 2 4 …
y=log2x … …
y=log x … …
1
2
-2 -1 0 1 2
2 1 0 -1 -2
2
1
-1
-2
1
2
4
0
y
x
3
y=log2x
y=log1/2x
两个图像关于x轴对称
画出对数函数 的图象
2
1
-1
-2
1
2
4
0
y
x
3
y=log2x
y=log1/2x
y=log3x
y=log1/3x
1.函数图象分布在哪些象限?
一、四
2.函数图象有哪些特殊点
(1,0)
3.函数图象的单调性与底数a的关系?
当0
y=logax(a>1)
y=logax(0
x
y
o
x
y
+∞
+∞
+∞
- ∞
+∞
- ∞
·
·
(1,0)
(1,0)
当x>1时,y>0;
当0
当x>1时,y<0
对数函数y= log a x(a>0,且a≠1)的图象与性质
o
x
y
1
o
x
y
1
定义域:( 0,+∞);值域:R.
定义域:( 0,+∞);值域:R.
过定点(1,0)即x=1时,y=0.
过定点(1,0)即x=1时,y=0.
当a>1时, x∈(0,1)y<0
x∈(1,+∞)时,y>0
当0
x∈(1,+∞)时,y<0
当a>1时,y=logax在( 0,+∞)
是增函数.
当0
非奇非偶
知识点二
a > 1
0 类型1 对数函数图像
角度一 对数型函数过定点问题
令对数型部分的真数为1,求出的x值为点的横坐标,
此时的函数值为点的纵坐标。
角度二 对数型函数图象的特征
例1.已知图中曲线C1,C2,C3,C4分别是函数y=loga x,y=logb x,y=logc x,y=logd x的图象,则a,b,c,d 的大小关系是( )
A.d
y
o
1
y=logax
y=logbx
y=logc x
y=logd x
B
作直线y=1与图像相交,从左至右,
底数依次增大
函数y=x+a与y=logax的图象只可能是下面选项中的( )
x
y
o
1
x
y
o
1
x
y
o
1
C
A
B
D
1
1
1
x
y
o
1
1
A中,由y=x+a的图象,知a>1,由y=logax的图象知0
D中,由y=x+a的图象,知a<0,由y=logax的图象知a>1,选项D不符合题意.
C
角度三 作对数型函数的图象
作出函数y=|lg(x-1)|的图象
先画出函数y=lg x的图象
x
y
o
1
1
再将该函数图象向右平移1个单位长度
得到函数y=lg(x-1)的图象
最后把y=lg(x-1)的图象在x轴下方的部分
对称翻折到x轴上方
类型2 对数函数的性质
1.比较大小
例2.比较下列各组中两个值的大小:
(1) log25.3 , log24.7 (2) log0.27 , logo.29
(3) log3π , logπ3
(4) loga3.1 , loga5.2(a>0,a≠1)
y=log2x在( 0,+∞) 是增
函数.log25.3 > log24.7
y=log0.2x在( 0,+∞) 是减
函数.log0.27 > logo.29
log3π>1,0
当0
比较两个对数式的大小,一般有三种方法:
(1)若是同底的对数,则可直接利用对数函数的单调性,只需比较两个真数的大小即可.
(2) 同真的利用对数函数的图象或用换底公式转化.
(3) 底数和真数都不同,找中间量.
若底数为同一参数,则根据底数对对数函数单调性的影响,
对底数进行分类讨论.
log23与log54
2.解含对数型不等式
例3. (1)解不等式log5(1-x)>log5(3x-2).
1-x>0
3x-2>0
1-x>3x-2
x<1
x>
2
3
x<
3
4
{x| <x< }
2
3
3
4
1
2
(4).解不等式:loga(x-4)>loga(x-2).
x-4>0
x-2>0
x-4>x-2
x-4>0
x-2>0
x-4
3.对数型函数的奇偶性和单调性
[解析] 由题意,得x2-3x-10>0,∴(x-5)(x+2)>0,∴x<-2或x>5.
令u=x2-3x-10,
函数f(x)的单调递增区间即为函数u=x2-3x-10在定义域上的
单调递减区间.
y=log u
1
2
例5.已知函数f(x)=loga(x+1)-loga(1-x)(a>0且a≠1).
(1)求f(x)的定义域;
(2)判断函数f(x)的奇偶性并加以证明.
(2)由(1)知函数f(x)的定义域为(-1,1)关于原点对称.
∴f(-x)=loga(-x+1)-loga(1+x)
=-[loga(1+x)-loga(1-x)]=-f(x),
∴函数f(x)为奇函数
若函数y=loga(2-ax)在x∈[0,1]上是减函数,则a的取值范围是( )
A.(0,1) B.(1,2)
C.(0,2) D.(1,+∞)
令u=2-ax,由于a>0且a≠1,所以u=2-ax为减函数,
又根据对数函数定义域要求u=2-ax在[0,1]
上恒大于零,当x∈[0,1]时,umin=2-a>0,解得a<2.
根据复合函数单调性“同增异减”法则,要使f(x)=loga(2-ax)
在[0,1]上为减函数,则需y=logau为增函数,所以a>1.
综上可得1
4.对数型函数的值域
[解析] (1)y=log2(x2+4)的定义域为R.∵x2+4≥4,
∴log2(x2+4)≥log24=2.
∴y=log2(x2+4)的值域为{y|y≥2}.
(2)设u=3+2x-x2,则u=-(x-1)2+4≤4.∵u>0,∴0
A.(0,+∞) B.[0,+∞)
C.(1,+∞) D.[1,+∞)
[解析] ∵3x+1>1,且f(x)在(1,+∞)上单调递增,
∴log2(3x+1)>log21=0,故该函数的值域为(0,+∞).
( )
( )
( )
知识点三
反函数
指数函数y=ax与对数函数y=logax(a>0,且a≠1)互为__________,
它们定义域与值域正好________.
反函数
互换
互为反函数的两个函数的单调性相同,但单调区间不一定相同.
互为反函数的两个函数的图象关于直线y=x对称.
例8:作出 y=log2x , y=log x , y=lgx的图象.
1
1
x
y
o
log
1
3
指数函数y=ax的反函数是对数函数y=logax.
∵对数函数y=logax的图象过点(9,2).
∴2=loga9,解得a=3.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
