数学人教A版(2019)必修第一册4.5.2 用二分法求方程的近似解 (共24张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.5.2 用二分法求方程的近似解 (共24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-13 19:35:53 | ||
图片预览







文档简介
(共24张PPT)
用二分法求方程的近似解
新课程标准 核心素养
1.探索用二分法求方程近似解的思路; 逻辑推理
2.能借助计算工具用二分法求方程近似解; 数学运算
3.了解用二分法求方程近似解具有一般性; 数学抽象
受第九号台风“利奇马”影响,八月十日夜间到十一日夜间滕州出现了暴雨并伴有大风天气,造成了荆河中路一段长2千米的电路发生了故障.如果你是一名维修工人如何迅速查出故障所在点?
生活中的二分法
放在银行门口电动车在早7:00到19:00,12小时内被盗,
正好被监控器拍到。请你化身为小侦探,用最快的方法检索
监控视频,将小偷逃跑时间提供给警察。
看商品,猜价格
游戏规则:
给出一件商品,请你猜出它的准确价格,我们给的提示只有“高了”和“低了”。给出的商品价格在100 ~ 200之间的整数,如果你能在规定的次数之内猜中
价格,这件商品就是你的了。
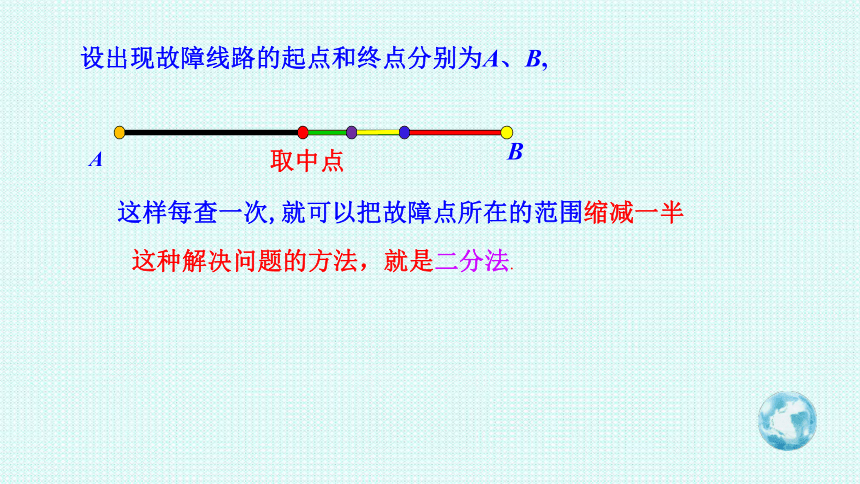
设出现故障线路的起点和终点分别为A、B,
A
B
取中点
这样每查一次,就可以把故障点所在的范围缩减一半
这种解决问题的方法,就是二分法.
知识点1
二分法的概念
对于在区间[a,b]上____________且_____________________的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到函数零点近似值的方法叫做二分法.
连续不断
f(a)·f(b)<0
是否所有的函数都可以用二分法求函数的零点?
思考1:
不是,只有满足函数图象在零点附近连续,且在该零点左右函数值异号时,才能应用“二分法”求函数零点.
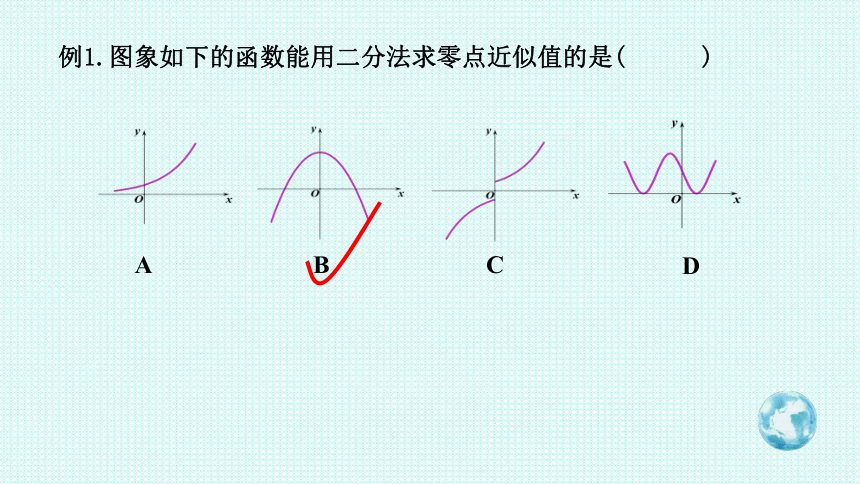
例1.图象如下的函数能用二分法求零点近似值的是( )
D
B
A
C
问题:你会解下列方程吗
2x-6=0; 2x2-3x+1=0; lnx+2x-6=0
lnx+2x-6=0,我们不会解这个方程,怎么办?我们会什么?
把方程lnx+2x-6=0等价变形为lnx= -2x+6
在同一直角坐标系内做函数y=lnx和y=-2x+6的图象.
y=lnx
y=-2x+6
观察图象可知,y=lnx和y=-2x+6的图象交点的横坐标x0∈(2,3). 而x0就是方程lnx+2x-6=0的实数根,进而就是函数f(x)=lnx+2x-6的零点
你会求方程lnx+2x-6=0的近似解吗
计算,f(2)=ln2+2×2-6= ln2-2= ln2- lne <0, f(3)=ln3+2×3-6ln3>ln1=0所以, f(2)·f(3)<0,根据函数零点存在性定理,x0∈(2,3)是正确的.
这只是确定了函数f(x)=lnx+2x-6的零点,即方程lnx+2x-6=0的
实数根的范围,这个x0的值究竟是多少呢?
可以转化为函数f(x)=lnx+2x-6在区间(2,3)内零点的近似值。
在已知存在零点的区间确定函数的零点的近似值,实际上就是如何
缩小零点所在的范围,或是如何得到一个更小的区间,使得零点
还在里面,从而得到零点的近似值
思考:如何缩小零点所在的区间?
对于一个已知零点所在区间[a,b],取其中点 c ,计算f(c),如果f(c)=0,那么 c 就是函数的零点;如果不为0,通过比较中点与两个端点函数值的正负情况,即可判断零点是在(a,c)内,还是在(c,b)内,从而将范围缩小了一半,以此方法重复进行……
f(x)=lnx+2x-6
∵f(2)<0, f(3)>0∴x0∈(2,3)
2.5
∵f(2.5)<0, f(3)>0∴x0∈(2.5,3)
2.75
∵f(2.5)<0, f(2.75)>0∴x0∈(2.5,2.75)
2.5
2.5
2.75
2.625
∵f(2.5)<0, f(2.625)>0∴x0∈(2.5,2.625)
2.5
2.625
∵f(2.5)<0, f(2.5625)>0∴x0∈(2.5,2.5625)
……
零点所在区间 中点的值 中点函数近似值
(2,3) 2.5 -0.084
(2.5,3) 2.75 0.512
(2.5,2.75) 2. 625 0.215
(2.5,2.625) 2.562 5 0.066
(2.5,2.5625) 2. 531 25 -0.009
(2.53125,2.5625) 2. 546 875 0.029
(2.53125,2.546875) 2. 539 062 5 0.010
(2.53125,2.5390625) 2. 535 156 25 0.001
也可以将x = 2.531 25作为函数f(x)=lnx+2x-6零点的近似值,也即方程
lnx+2x-6=0的近似解.
例如,当精确度为0.01时,因为|2.539 062 5-2.531 25|=0.007 812 5<0.01,
所以区间(2.531 25, 2.539 062 5)内任意一点都可以作为零点的近似值,
二分法求函数y=f(x)零点的步骤:
知识点2
(1) 确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;
(2) 求区间(a,b)的中点c;
(3) 计算f(c) ;
若f(c)=0,则c就是函数的零点c ;
若f(a)·f(c)<0,则令b=c(此时零点x0∈(a,c));
若f(b)·f(c)<0,则令a=c(此时零点x0∈(c,b));
(4) 判断是否达到精度ε,若|a-b|<ε,则得到零点近似值a(或b),
否则重复(2) (3) (4) ;
例1. 借助信息技术,用二分法求方程 2x+3x=7函数的近似解
(精确度为0.1)
解:原方程即2x+3x-7=0 ,令f(x) =2x+3x-7,用信息技术画出函数y=f(x)的图象,并列出它的对应值表.
x 0 1 2 3 4 5 6 7 8
y -6 -2 3 10 21 40 75 142 273
观察函数图象和上表,可知f(1)·f(2)<0.
取区间(1,2)的中点x1=1.5,f(1.5)≈ 0.33,因为f(1)·f(1.5)<0,
所以x0 ∈(1,1.5),取区间(1,1.5)的中点x2=1.25 ,
f(1.25)≈-0.87,因为f(1.25)·f(1.5)<0,所以x0∈(1.25,1.5)同理可得,
x0∈(1.375,1.5),x0∈(1.375,1.437 5),
由于|1.375-1.437 5|=0.062 5<0.1,所以,原方程的近似解可取为1.437 5.
判断方程lg x=3-x解的个数,并说明理由,若有解,用二分法求其近似解.(精确度0.1).
解:画出g(x)=lgx及h(x)=3-x的图象,观察图象得,方程lgx=3-x有唯一解,记为x1,且这个解在区间(2,3)内.
y
1
3
3
x
o
设 f(x)=lgx+x-3,因为f(x)在定义域内为增函数且f(2)<0,f(3)>0,所以f(x)在(2,3)有唯一零点,方程lg x=3-x有唯一解
列出下表:
根所在区间 区间端点函数值符号 中点值 中点函数值符号
(2,3)
(2.5,3)
(2.5,2.75)
(2.5,2.625)
(2.562 5,2.625)
f(2)<0,f(3)>0
f(2.5)<0,f(3)>0
f(2.5)<0,f(2.75)>0
f(2.5)<0,f(2.625)>0
f(2.562 5)<0,
f(2.625)>0
2.5
2.75
2.625
2.562 5
f(2.5)<0
f(2.75)>0
f(2.625)>0
f(2.562 5)<0
因为|2.625-2.562 5|=0.062 5<0.1,所以可以将x=2.625作为原方程的一个近似解.
1.用二分法求函数f(x)=x3+5的零点可以取的初始区间是( )
A.[-2,1] B.[-1,0]
C.[0,1] D.[1,2]
2.在用二分法求函数f(x)的一个正实数零点时,经计算,f(0.64)<0,f(0.72)>0,f(0.68)<0,则函数的一个精确到0.1的正实数零点的近似值为 ( )
A.0.68 B.0.72
C.0.7 D.0.6
精确到0.1所取的近似值都是0.7
已知f(0.64)<0,f(0.72)>0,则函数f(x)的零点
的初始区间为(0.64,0.72),又因为0.68= ×(0.64+0.72),且f(0.68)<0,所以零点在区间
(0.68,0.72)上
1
2
3.用二分法研究函数f(x)=x3+3x-1的零点时,第一次经计算得f(0)<0,f(0.5)>0,可得其中一个零点x0∈________,第二次应计算________.
(0,0.5)
f(0.25)
4.函数f(x)=x2+ax+b有零点,但不能用二分法求出,则a,b的关系是____________.
解析:∵函数f(x)=x2+ax+b有零点,但不能用二分法,∴函数f(x)=x2+ax+b图象与x轴有且仅有一个交点.∴Δ=a2-4b=0.∴a2=4b.
a2=4b
5.某方程有一无理根在区间D=(1,3)内,若用二分法求此根的近似值,将D等分________次后,所得近似值可精确到0.1.
5
6.方程3x+m=0的根在(-1,0)内,则m的取值范围为________.
[解析] 解法一:∵f(x)=3x+m单调递增,∴只要满足
( )
0(0,3)
解法二:由3x+m=0得m=-3x,∵x∈(-1,0),∴-3x∈(0,3),
二分法思想的实际应用
问题:现有12个小球,体积均匀外表一致,但是其中有一个小球却比别的球重。如果给你一天平,最少要称几次才可以找出这个比较重的球?
第一次,两端各放6个小球,低的那一端一定有重球;
第二次,两端各放3个小球,低的那一端一定
有重球;
第三次,两端各放1个小球,
如果平衡,剩下的就是重球;
如果不平衡,则低的那一端
就是重球。
某娱乐节目有一个给选手在限定时间内猜一物品的售价的环节,某次猜一品牌手机的价格,手机价格在500~1 000元,选手开始报价1 000元,主持人回答高了;紧接着报900元,高了;700元,低了;800元,低了;880元,高了;850元,低了;851元,恭喜你猜中了,
[解析] 取价格区间[500,1 000]的中点750元,低了;
就再取[750,1 000]的中点875,高了;就取[750,875]
的中点,遇到小数,则取整数,照此猜下去,可以猜价:
750,875,812,843,859,851,经过6次即能猜中价格
证明方程6-3x=2x在(1,2)内有惟一一个实数解,并求出这个实数解的一个近似值(精确到0.1).
设f(x)=6-3x-2x,
∵f(1)=6-3-2=1>0,f(2)=6-6-22=-4<0,
∴f(1)·f(2)<0又f(x)在定义域内是减函数,
故方程在(1,2)内有惟一的解.
中点的值 中点函数值的符号 取区间
=1.5 f(1.5)<0 (1,1.5)
=1.25 f(1.25)<0 (1,1.25)
=1.125 f(1.125)>0 (1.125,1.25)
=1.187 5 f(1.187 5)>0 (1.187 5,1.25)
=1.218 75 f(1.218 75)>0 (1.218 75,1.25)
=1.234 375 f(1.234 375)<0 (1.218 75,1.234 375)
用二分法求方程的近似解
新课程标准 核心素养
1.探索用二分法求方程近似解的思路; 逻辑推理
2.能借助计算工具用二分法求方程近似解; 数学运算
3.了解用二分法求方程近似解具有一般性; 数学抽象
受第九号台风“利奇马”影响,八月十日夜间到十一日夜间滕州出现了暴雨并伴有大风天气,造成了荆河中路一段长2千米的电路发生了故障.如果你是一名维修工人如何迅速查出故障所在点?
生活中的二分法
放在银行门口电动车在早7:00到19:00,12小时内被盗,
正好被监控器拍到。请你化身为小侦探,用最快的方法检索
监控视频,将小偷逃跑时间提供给警察。
看商品,猜价格
游戏规则:
给出一件商品,请你猜出它的准确价格,我们给的提示只有“高了”和“低了”。给出的商品价格在100 ~ 200之间的整数,如果你能在规定的次数之内猜中
价格,这件商品就是你的了。
设出现故障线路的起点和终点分别为A、B,
A
B
取中点
这样每查一次,就可以把故障点所在的范围缩减一半
这种解决问题的方法,就是二分法.
知识点1
二分法的概念
对于在区间[a,b]上____________且_____________________的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到函数零点近似值的方法叫做二分法.
连续不断
f(a)·f(b)<0
是否所有的函数都可以用二分法求函数的零点?
思考1:
不是,只有满足函数图象在零点附近连续,且在该零点左右函数值异号时,才能应用“二分法”求函数零点.
例1.图象如下的函数能用二分法求零点近似值的是( )
D
B
A
C
问题:你会解下列方程吗
2x-6=0; 2x2-3x+1=0; lnx+2x-6=0
lnx+2x-6=0,我们不会解这个方程,怎么办?我们会什么?
把方程lnx+2x-6=0等价变形为lnx= -2x+6
在同一直角坐标系内做函数y=lnx和y=-2x+6的图象.
y=lnx
y=-2x+6
观察图象可知,y=lnx和y=-2x+6的图象交点的横坐标x0∈(2,3). 而x0就是方程lnx+2x-6=0的实数根,进而就是函数f(x)=lnx+2x-6的零点
你会求方程lnx+2x-6=0的近似解吗
计算,f(2)=ln2+2×2-6= ln2-2= ln2- lne <0, f(3)=ln3+2×3-6ln3>ln1=0所以, f(2)·f(3)<0,根据函数零点存在性定理,x0∈(2,3)是正确的.
这只是确定了函数f(x)=lnx+2x-6的零点,即方程lnx+2x-6=0的
实数根的范围,这个x0的值究竟是多少呢?
可以转化为函数f(x)=lnx+2x-6在区间(2,3)内零点的近似值。
在已知存在零点的区间确定函数的零点的近似值,实际上就是如何
缩小零点所在的范围,或是如何得到一个更小的区间,使得零点
还在里面,从而得到零点的近似值
思考:如何缩小零点所在的区间?
对于一个已知零点所在区间[a,b],取其中点 c ,计算f(c),如果f(c)=0,那么 c 就是函数的零点;如果不为0,通过比较中点与两个端点函数值的正负情况,即可判断零点是在(a,c)内,还是在(c,b)内,从而将范围缩小了一半,以此方法重复进行……
f(x)=lnx+2x-6
∵f(2)<0, f(3)>0∴x0∈(2,3)
2.5
∵f(2.5)<0, f(3)>0∴x0∈(2.5,3)
2.75
∵f(2.5)<0, f(2.75)>0∴x0∈(2.5,2.75)
2.5
2.5
2.75
2.625
∵f(2.5)<0, f(2.625)>0∴x0∈(2.5,2.625)
2.5
2.625
∵f(2.5)<0, f(2.5625)>0∴x0∈(2.5,2.5625)
……
零点所在区间 中点的值 中点函数近似值
(2,3) 2.5 -0.084
(2.5,3) 2.75 0.512
(2.5,2.75) 2. 625 0.215
(2.5,2.625) 2.562 5 0.066
(2.5,2.5625) 2. 531 25 -0.009
(2.53125,2.5625) 2. 546 875 0.029
(2.53125,2.546875) 2. 539 062 5 0.010
(2.53125,2.5390625) 2. 535 156 25 0.001
也可以将x = 2.531 25作为函数f(x)=lnx+2x-6零点的近似值,也即方程
lnx+2x-6=0的近似解.
例如,当精确度为0.01时,因为|2.539 062 5-2.531 25|=0.007 812 5<0.01,
所以区间(2.531 25, 2.539 062 5)内任意一点都可以作为零点的近似值,
二分法求函数y=f(x)零点的步骤:
知识点2
(1) 确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;
(2) 求区间(a,b)的中点c;
(3) 计算f(c) ;
若f(c)=0,则c就是函数的零点c ;
若f(a)·f(c)<0,则令b=c(此时零点x0∈(a,c));
若f(b)·f(c)<0,则令a=c(此时零点x0∈(c,b));
(4) 判断是否达到精度ε,若|a-b|<ε,则得到零点近似值a(或b),
否则重复(2) (3) (4) ;
例1. 借助信息技术,用二分法求方程 2x+3x=7函数的近似解
(精确度为0.1)
解:原方程即2x+3x-7=0 ,令f(x) =2x+3x-7,用信息技术画出函数y=f(x)的图象,并列出它的对应值表.
x 0 1 2 3 4 5 6 7 8
y -6 -2 3 10 21 40 75 142 273
观察函数图象和上表,可知f(1)·f(2)<0.
取区间(1,2)的中点x1=1.5,f(1.5)≈ 0.33,因为f(1)·f(1.5)<0,
所以x0 ∈(1,1.5),取区间(1,1.5)的中点x2=1.25 ,
f(1.25)≈-0.87,因为f(1.25)·f(1.5)<0,所以x0∈(1.25,1.5)同理可得,
x0∈(1.375,1.5),x0∈(1.375,1.437 5),
由于|1.375-1.437 5|=0.062 5<0.1,所以,原方程的近似解可取为1.437 5.
判断方程lg x=3-x解的个数,并说明理由,若有解,用二分法求其近似解.(精确度0.1).
解:画出g(x)=lgx及h(x)=3-x的图象,观察图象得,方程lgx=3-x有唯一解,记为x1,且这个解在区间(2,3)内.
y
1
3
3
x
o
设 f(x)=lgx+x-3,因为f(x)在定义域内为增函数且f(2)<0,f(3)>0,所以f(x)在(2,3)有唯一零点,方程lg x=3-x有唯一解
列出下表:
根所在区间 区间端点函数值符号 中点值 中点函数值符号
(2,3)
(2.5,3)
(2.5,2.75)
(2.5,2.625)
(2.562 5,2.625)
f(2)<0,f(3)>0
f(2.5)<0,f(3)>0
f(2.5)<0,f(2.75)>0
f(2.5)<0,f(2.625)>0
f(2.562 5)<0,
f(2.625)>0
2.5
2.75
2.625
2.562 5
f(2.5)<0
f(2.75)>0
f(2.625)>0
f(2.562 5)<0
因为|2.625-2.562 5|=0.062 5<0.1,所以可以将x=2.625作为原方程的一个近似解.
1.用二分法求函数f(x)=x3+5的零点可以取的初始区间是( )
A.[-2,1] B.[-1,0]
C.[0,1] D.[1,2]
2.在用二分法求函数f(x)的一个正实数零点时,经计算,f(0.64)<0,f(0.72)>0,f(0.68)<0,则函数的一个精确到0.1的正实数零点的近似值为 ( )
A.0.68 B.0.72
C.0.7 D.0.6
精确到0.1所取的近似值都是0.7
已知f(0.64)<0,f(0.72)>0,则函数f(x)的零点
的初始区间为(0.64,0.72),又因为0.68= ×(0.64+0.72),且f(0.68)<0,所以零点在区间
(0.68,0.72)上
1
2
3.用二分法研究函数f(x)=x3+3x-1的零点时,第一次经计算得f(0)<0,f(0.5)>0,可得其中一个零点x0∈________,第二次应计算________.
(0,0.5)
f(0.25)
4.函数f(x)=x2+ax+b有零点,但不能用二分法求出,则a,b的关系是____________.
解析:∵函数f(x)=x2+ax+b有零点,但不能用二分法,∴函数f(x)=x2+ax+b图象与x轴有且仅有一个交点.∴Δ=a2-4b=0.∴a2=4b.
a2=4b
5.某方程有一无理根在区间D=(1,3)内,若用二分法求此根的近似值,将D等分________次后,所得近似值可精确到0.1.
5
6.方程3x+m=0的根在(-1,0)内,则m的取值范围为________.
[解析] 解法一:∵f(x)=3x+m单调递增,∴只要满足
( )
0
解法二:由3x+m=0得m=-3x,∵x∈(-1,0),∴-3x∈(0,3),
二分法思想的实际应用
问题:现有12个小球,体积均匀外表一致,但是其中有一个小球却比别的球重。如果给你一天平,最少要称几次才可以找出这个比较重的球?
第一次,两端各放6个小球,低的那一端一定有重球;
第二次,两端各放3个小球,低的那一端一定
有重球;
第三次,两端各放1个小球,
如果平衡,剩下的就是重球;
如果不平衡,则低的那一端
就是重球。
某娱乐节目有一个给选手在限定时间内猜一物品的售价的环节,某次猜一品牌手机的价格,手机价格在500~1 000元,选手开始报价1 000元,主持人回答高了;紧接着报900元,高了;700元,低了;800元,低了;880元,高了;850元,低了;851元,恭喜你猜中了,
[解析] 取价格区间[500,1 000]的中点750元,低了;
就再取[750,1 000]的中点875,高了;就取[750,875]
的中点,遇到小数,则取整数,照此猜下去,可以猜价:
750,875,812,843,859,851,经过6次即能猜中价格
证明方程6-3x=2x在(1,2)内有惟一一个实数解,并求出这个实数解的一个近似值(精确到0.1).
设f(x)=6-3x-2x,
∵f(1)=6-3-2=1>0,f(2)=6-6-22=-4<0,
∴f(1)·f(2)<0又f(x)在定义域内是减函数,
故方程在(1,2)内有惟一的解.
中点的值 中点函数值的符号 取区间
=1.5 f(1.5)<0 (1,1.5)
=1.25 f(1.25)<0 (1,1.25)
=1.125 f(1.125)>0 (1.125,1.25)
=1.187 5 f(1.187 5)>0 (1.187 5,1.25)
=1.218 75 f(1.218 75)>0 (1.218 75,1.25)
=1.234 375 f(1.234 375)<0 (1.218 75,1.234 375)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
